農用植保無人機避障噴施路徑規劃方法及無人機與流程
本發明涉及一種農用植保無人機避障噴施路徑規劃方法及無人機,屬于無人機路線規劃方法及控制方法領域。
背景技術:
植保無人機噴施作業的區域一般面積較大,而無人機體積小,反應靈活,所以一般植保無人機噴施的路線被規劃成來回往復的形如“Π”的形狀,其路線如圖3所示,圖3(a)是標準的矩形噴施區域,圖3(b)是一個不規則的噴施區域,但是他們規劃的路線都是來回往復的。這種來回往復的路線在沒有障礙的情況下噴施作業的效率和噴灑的均勻度(重噴和漏噴)都特別好。但是在實際應用中這種無任何障礙的無人機噴灑作業幾乎不存在。植保無人機在噴施作業中很有可能遇到零散分布的樹木,信號塔,電線桿等障礙。這無可避免的會涉及到植保無人機的噴施過程的避障問題。
一般植保無人機在噴施作業中遇到的情況如圖4所示(其中圓形代表障礙),在已經離線規劃好的路線中分布著若干障礙,這些障礙的特點是比較小,也比較分散,在離線路線規劃其中很難將其排除,此時就要求無人機在噴施作業的過程中還要進行障礙的躲避。
以無人機在噴施作業中只遇到一個障礙的情況為例,運用傳統的避障算法所得到的避障路線如圖5所示。由圖5看出,無人機在避障的同時進行噴灑作業,因為無人機在躲避障礙的時候不能停止噴施作業,所以就會導致有些區域噴灑不到農藥(如上面的漏噴區域),有些區域會在無人機回飛時噴灑兩遍(如上面的重復噴灑區域)。此避障過程會導致大面積的重噴和漏噴,下面就無人機噴施作業中的避障問題展開討論,并提出一種兼顧路徑長短和多噴漏噴的方法。給出一種無人機在噴施作業中的避障策略,這種避障策略可以在路徑長度增加不多的情況下,有效的減少多噴和漏噴的面積。圖5是以單障礙為例,當遇到多個障礙時,傳統的避障算法將會導致更多的重噴和漏噴的面積。
文獻“《基于Dubins路徑的無人機避障規劃算法》,關震宇”提供了一種無人機避障規劃方法,但其未排除不需要躲避的障礙,并且不能返回原飛行路線上,從而導致其不能在減少重噴漏噴面積的基礎上選擇最佳路徑。
技術實現要素:
本發明的目的是為了解決現有技術中的避障算法未能兼顧減少路徑長短以及減少重噴漏噴的缺點,而提出一種新的用于植保無人機的避障路徑規劃方法及無人機。
一種用于植保無人機的避障噴施路徑長度確定方法,所述方法用于規劃從起始點到終點的飛行路徑,所述飛行路徑包括M條噴施路徑以及N條轉彎路徑,其特征在于,確定第一條噴施路徑的方法包括:
步驟1)從第一條直線噴施路徑起,將當前飛行路徑的起點和終點連接,形成一條用于表示原飛行路線的直線段;
步驟2)判斷所述直線段是否與障礙圓相交,若不相交,則按原路線直線飛行,若相交,則執行步驟3);所述障礙圓是用于表示障礙物位置和大小特征的模型;將與所述直線段相交的障礙圓稱為目標障礙圓;
步驟3)比較無人機的最小轉彎半徑與所述障礙圓的半徑大小;
若障礙圓的半徑大于等于無人機的最小轉彎半徑,則執行步驟4);
若障礙圓的半徑小于無人機的最小轉彎半徑,則生成兩個所述障礙圓的內切圓,以內切圓代替所述障礙圓,然后執行步驟4);所述內切圓的圓心位于所述直線段的經過所述障礙圓圓心的垂線上,所述內切圓的半徑等于所述最小轉彎圓的半徑;
步驟4)生成復數個與所述直線段與所述障礙圓同時相切的最小轉彎圓;所述最小轉彎圓的半徑為無人機的最小轉彎半徑;
步驟5)根據所述直線段、所述目標障礙圓以及所述最小轉彎圓確定復數個可選的飛行路徑并計算路徑的長度以及與所述的可選飛行路徑對應的重噴漏噴面積,并將數據進行歸一化處理;
步驟6)將所述的復數個可選路徑作為初始種群,計算出適應值的大小;
步驟7)使用遺傳算法的選擇、交叉、變異操作,當滿足迭代次數或者滿足預定的適應值大小條件時,輸出最佳的搜索路徑。
步驟8)計算無人機從當前噴施路徑的終點飛行到下一條噴施路徑的起點所需經過的轉彎路徑的長度;
步驟9):重復執行步驟1)至步驟8),通過每一次執行得到的計算結果計算出總的飛行路徑長度以及重噴漏噴面積。
本發明還包括一種無人機,包括:
路徑存儲裝置,用于預先存儲已規劃完成的預定飛行路徑信息;
障礙檢測裝置,用于實時檢測周圍的障礙物信息,并預測是否會與障礙物碰撞;
判斷裝置,用于在障礙檢測模塊預測會與障礙物碰撞時,發出避障信號;
避障噴施路徑確定裝置,用于在未接收到避障信號時,從所述路徑存儲模塊中讀取所 述預定飛行路徑信息,并發送至飛行控制裝置;還用于在接收到避障信號時,實現如權利要求7或8中任意一項裝置所述的功能,并將所述最佳路徑信息發送至飛行控制裝置;
飛行控制裝置,用于根據接收到的路徑信息控制無人機進行飛行。
本發明的有益效果為:使用Dubins路徑算法生成的避障路徑相比較于現有技術的避障算法更符合無人機的飛行特性;使用起點至終點的連線來排除不需要躲避的障礙,在多障礙噴施路徑選擇時采用啟發式的遺傳算法搜索路徑搜索最優路徑時用時更少;在已知障礙的情況下,相比較現有技術可以大大減少重噴漏噴的面積,一般可以減少200%至400%。
附圖說明
圖1為本發明的用于植保無人機的避障路徑規劃方法的流程圖;
圖2為本發明的無人機的方框原理圖;
圖3(a)為無人機在無障礙的矩形區域進行噴施的路線示意圖;
圖3(b)為無人機在無障礙的不規則區域進行噴施的路線示意圖;
圖4(a)為無人機在有障礙的矩形區域進行噴施的路線示意圖;
圖4(b)為無人機在有障礙的不規則區域進行噴施的路線示意圖;
圖5為現有技術的避障算法的避障路線圖;
圖6為本發明的障礙圓及障礙圓區域半徑的示意圖;
圖7為本發明的第一條飛行路徑上具有多障礙圓的實施例的示意圖;
圖8為本發明的通過遺傳算法和Dunbins路徑最終確定的避障路徑的示意圖;
圖9為當無人機的最小轉彎半徑小于噴施半徑時的飛行路線示意圖;
圖10為使用本發明的方法得到的避障路線的一個實施例的示意圖;
圖11為本發明的障礙圓與最小轉彎圓構成的三角形區域的示意圖;
圖12為本發明的無人機的避障流程圖;
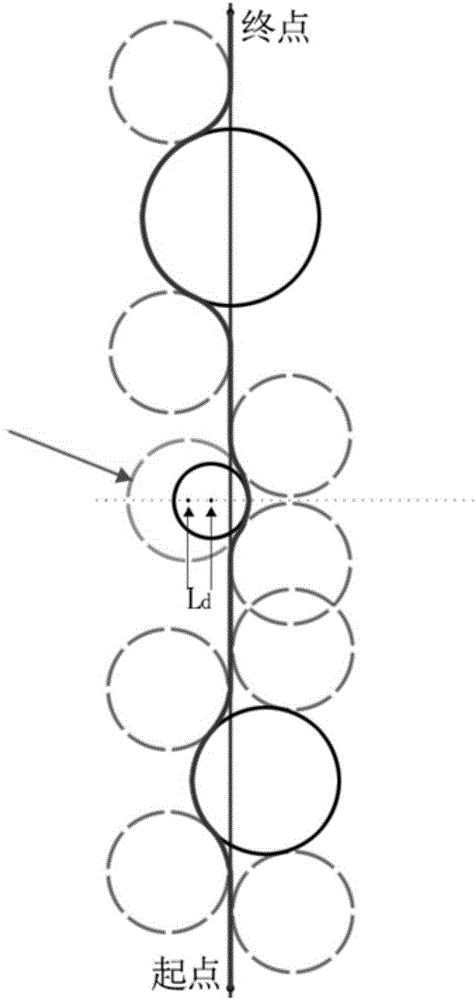
圖13為本發明的當障礙圓半徑小于最小轉彎半徑時的示意圖;
圖14為圖13的局部放大圖。
具體實施方式
具體實施方式一:本實施方式的用于植保無人機的避障路徑規劃方法,方法用于規劃飛行路徑,飛行路徑包括至少一條直線噴施路徑以及至少一條轉彎路徑,每一條直線噴施路徑包括一個起點和一個終點,每一條轉彎路徑表示從一個直線噴施路徑的終點飛行至下一個直線噴施路徑的起點的路徑,其特征在于,方法包括:
步驟1)從第一條直線噴施路徑起,將當前飛行路徑的起點和終點連接,形成一條用 于表示原飛行路線的直線段;
步驟2)判斷直線段是否與障礙圓相交,若不相交,則按原路線直線飛行,若相交,則執行步驟3);障礙圓是用于表示障礙物位置和大小特征的模型;將與直線段相交的障礙圓稱為目標障礙圓;
步驟3)比較無人機的最小轉彎半徑與障礙圓的半徑大小;
若障礙圓的半徑大于等于無人機的最小轉彎半徑,則執行步驟4);
若障礙圓的半徑小于無人機的最小轉彎半徑,則生成兩個障礙圓的內切圓,以內切圓代替障礙圓,然后執行步驟4);內切圓的圓心位于直線段的經過障礙圓圓心的垂線上,內切圓的半徑等于最小轉彎圓的半徑;
步驟4)生成復數個與直線段與障礙圓同時相切的最小轉彎圓;最小轉彎圓的半徑為無人機的最小轉彎半徑;
步驟5)根據直線段、目標障礙圓以及最小轉彎圓確定復數個可選的飛行路徑并計算路徑的長度以及與可選飛行路徑對應的重噴漏噴面積,并將數據進行歸一化處理;
步驟6)將所述的復數個可選路徑作為初始種群,計算出適應值的大小;
步驟7)使用遺傳算法的選擇、交叉、變異操作,當滿足迭代次數或者滿足預定的適應值大小條件時,輸出最佳的搜索路徑。
步驟8)計算無人機從當前噴施路徑的終點飛行到下一條噴施路徑的起點所需經過的轉彎路徑的長度;
步驟9):重復執行步驟1)至步驟8),通過每一次執行得到的計算結果計算出總的飛行路徑長度以及重噴漏噴面積。
步驟3)考慮到障礙圓的半徑小于無人機的最小轉彎半徑的情形,“小障礙”的表述意味著本發明主題的技術手段考慮到了障礙圓的半徑較小的情形。
圖13中出現了一個小于最小轉彎圓的障礙(虛線圓為最小轉彎圓),此時的處理方法是:過此小障礙圓的圓心,做與ST垂直的直線,以最小轉彎圓的大小為大小,作此障礙圓的內切圓,內切圓的圓心落在之前做的垂線上,這樣的內切圓有兩個,分別以這兩個內切圓的切點加入到有向圖中,作為兩個頂點,進行最佳路徑的搜索。當障礙圓的半徑小于最小轉彎圓時,后續所有的計算中都使用內切圓來代替障礙圓,或者說將內切圓視為原障礙圓。
圖14是圖13的局部放大圖,從圖14中可以看出,障礙圓的內切圓可以做出兩個,內切圓的圓心均位于障礙圓圓心與直線段所確定的垂線上。
具體實施方式二:本實施方式與具體實施方式一不同的是:
步驟5)中每條可選路徑的飛行路徑的長度通過如下公式計算:
其中N為單條路徑上必須躲避的障礙總數,N1是障礙圓與最小轉彎圓異側的障礙圓個數,N2是障礙圓與最小轉彎圓同側的障礙圓個數,且滿足N1+N2=N;其中b為直線段的長度;Rz為無人機的最小轉彎半徑;
當障礙圓的半徑大于等于無人機的最小轉彎半徑時,Ld為障礙圓的圓心到直線段的距離,Ri為障礙圓的半徑;
當障礙圓的半徑小于無人機的最小轉彎半徑時,Ld為內切圓的圓心到直線段的距離,Ri代表最小轉彎半徑的大小;
障礙圓半徑Ri滿足公式Ri=Rd+Rl,其中Rd為障礙圓的中心到最邊緣的距離,Rl為無人機需要與障礙物保持的安全距離。
其它步驟及參數與具體實施方式一相同。
具體實施方式三:本實施方式與具體實施方式一或二不同的是:
步驟5)中每條所述可選路徑的重噴漏噴面積通過如下公式計算:
其它步驟及參數與具體實施方式一或二相同。
具體實施方式四:本實施方式與具體實施方式一至三之一不同的是:
步驟8)用于根據如下公式計算轉彎路徑的長度D轉:
D轉=2Rp-2Rz+πRz
其中Rp為無人機噴灑的半徑。
其它步驟及參數與具體實施方式一至三之一相同。
具體實施方式五:本實施方式與具體實施方式一至四之一不同的是:
步驟9)中通過每一次執行得到的計算結果計算出總的飛行路徑長度具體為:
其中,M為直線噴施路徑的個數,K1為所有直線噴施路徑中障礙圓與最小轉彎圓異側的障礙圓個數,K2為所有直線噴施路徑中障礙圓與最小轉彎圓同側的障礙圓個數。
其它步驟及參數與具體實施方式一至四之一相同。
具體實施方式六:步驟9)中通過每一次執行得到的計算結果計算出總的重噴漏噴面積具體為:
其它步驟及參數與具體實施方式一至五之一相同。
具體實施方式七:遺傳算法的染色體基因對應于頂點,頂點的確定方法為:
過每個障礙圓的圓心,作直線段的垂線,垂線與障礙圓形成2個交點;將所有交點與飛行路徑的起點與終點的集合作為頂點的集合;
設K為障礙圓的個數,則頂點集中有2+2K個頂點;
染色體編碼從第1位到第2k+2位分別表示選擇原飛行路徑的起點、第1個障礙圓左側的路徑、選擇第1個障礙圓右側的路徑、選擇第2個障礙圓左側的路徑……選擇第k個圓的右側路徑、原飛行路徑的終點。
即這2+2K個頂點其中的2表示起點和終點,2K表示K個障礙圓都有左側的路徑和右側的路徑。規定頂點的概念是為了將無人機避障問題轉化為圖論,以便進一步使用遺傳算法解決該問題。也就是說將每個障礙圓的左側路徑和右側路徑分別都視為一個圖論中的頂點,那么一組從起點經過每個障礙圓的左側路徑或右側路徑,再到達終點的過程就可以用從起始點到每個頂點,最后再到終點的一組有向圖的路徑來表示。因此上述的頂點確定方式還有很多種,本實施方式僅舉出一個具體的例子,只要選取的頂點能夠唯一對應一個障礙圓的左側路徑或右側路徑即可,本發明不做限制。
例如,在一個實施例中,染色體編碼如下
其中,D后面第一位代表第幾個障礙,第二位代表該障礙的左側或右側,左側為1,右側為2。例如,D12表示遇到第一個障礙時選取障礙圓右側的曲線作為飛行軌跡,D31表示遇到第三個障礙時選取障礙圓左側的曲線作為飛行軌跡。
因此,上述實施例的路徑可以表示為“起點→D11→D22→D32→終點”,其染色體描述為(1,2,5,7,8)。
適應度函數為路徑的長短和重噴漏噴面積歸一化之后和的倒數,適應值越大則表示適應度越好。
其它步驟及參數與具體實施方式一至六之一相同。
具體實施方式八:本實施方式與具體實施方式七不同的是:
遺傳算法的適宜度函數為:
其中Fitness(i)為第i條路徑的適宜度,D(xi)和S(xi)分表代表路徑長度歸一化后的數據以及重噴漏噴面積歸一化后的數據;β1、β2分別代表路徑長度和重噴漏噴面積的權重;
路徑長度和重噴漏噴面積采用的數據歸一化函數為:
其中x為待處理的數據,x*為經過歸一化處理后的數據。即將路徑長度或重噴漏噴面積作為x帶入上述公式,可以得到D(xi)或S(xi)。x*在這里就是D(xi)或S(xi)。
其它步驟及參數與具體實施方式七相同。
具體實施方式九:本實施方式提供一種無人機,如圖2所示,包括:
路徑存儲裝置11,用于預先存儲已規劃完成的預定飛行路徑信息;
障礙檢測裝置12,用于實時檢測周圍的障礙物信息,并預測是否會與障礙物碰撞;
判斷裝置13,用于在障礙檢測模塊預測會與障礙物碰撞時,發出避障信號;
避障噴施路徑確定裝置14,用于在未接收到避障信號時,從路徑存儲模塊中讀取預定飛行路徑信息,并發送至飛行控制裝置;還用于在接收到避障信號時,實現如具體實施方式一至八中任意所述的方法所對應的功能,并將最佳路徑信息發送至飛行控制裝置;
飛行控制裝置,用于根據接收到的路徑信息控制無人機進行飛行。
<實施例>
本實施例主要涉及具體實施方式中出現公式的推導過程。
一、符號定義:
假設植保無人機在一塊具有若干個障礙的矩形地面上進行噴施作業(其他情況也是相似),假設矩形的長為a,寬為b,無人機的起點命名為S,終點命名為T。無人機來回往復的路線一共M條。
植保無人機噴施作業時的相關參數為:植保無人機的噴灑半徑為Rp,飛行速度V,植保無人機的最小轉彎半徑Rz,障礙圓的中心到最邊緣的距離為Rd,植保無人機的與障礙物的安全飛行距離Rl,所以,障礙圓的障礙區域半徑Ri=Rd+Rl。
部分定義如圖6所示。
二、數學分析
取圖4(a)中植保無人機來回往復路線上的第一條飛行路徑為例,在該路線上當遇到多障礙時,處理方法如下:
如圖7所示,該路線上一共有五個大小位置不一的障礙,要得到較優的避障路線一方面要考慮避障路徑的長短,另一方面還要盡量減少重噴漏噴的面積。該問題的求解算法描述如下。
步驟一:過起點S終點P做一條直線段,此線段將障礙圓模型分為兩類
1類、障礙圓模型與直線不相交,說明該障礙圓不在原規劃的飛行路徑上,即不影響之前規劃的飛行路徑,在規劃路線時就不予考慮此類障礙;
2類、障礙圓模型與直線相交,即障礙圓在飛行路線上,阻擋正常飛行,規劃路線時主要考慮此類障礙;
步驟二:若所有障礙屬于1類障礙則按照原路線飛行,若出現障礙圓模型屬于2類障礙則采用的是Dubins路徑生成避障路線。方法是:首先確定障礙圓的位置和大小以及根據最小轉彎半徑生成最小轉彎圓;然后,以最小轉彎圓的大小為大小,做出同時與障礙圓和原路線ST相切的最小轉彎圓,這樣的最小轉彎圓一共可以生成四個,最后生成可飛路徑,由于上圖中有三個必須多必的障礙,所以會生成八條可飛路徑,逐一計算路徑的長短即可選出最佳路徑。
但是上述的只是三個障礙的情況,當障礙一旦增加若干,則可飛路徑將會驟然增多,對于此類問題,本文采取的方法如下。
當遇到多障礙時問題轉化為轉化為多障礙環境下的避障問題,即找到一條從起點S到終點T的適合植保無人機噴施作業的飛行曲線路徑,即路徑S-(障礙圓1-障礙圓n)-T 的路徑,其求解可以歸納如下
在已知無人機出發點S,初始速度向量V,終點T,終點速度向量也是V,最小轉彎半徑Rz,障礙圓模型Dk(k=0,1,2,3…n)的位置情況下,求解從點S到T,滿足植保無人機飛行最小轉彎半徑約束的可避開障礙的安全飛行路徑,即求取從起始點S到終點T滿足最小轉彎半徑約束的有向曲線。
由Dubins路徑的生成方法知,該曲線是一條與n(n=[1,k])個障礙圓相切的曲線,如果將起始圓和終點圓作為一個有向圖的起點和終點,過障礙圓圓心Dk做直線且與飛行路線垂直,該直線與障礙圓有左右兩個交點,以這兩個交點作為圖中的各個頂點,則可構建有向圖G=(V,A),其中V為數量為2*k+2的非空頂點集,A為有向路徑的集合。則本題轉化為求有向路徑(S,T)=(S,W,T)的問題,其中W為由該有向曲線遍歷的各個點組成的集合,W中各個點的順序表明了其被遍歷的順序。
運用遺傳算法和Dubins路徑的方法最終搜索到無人機噴施作業中避障路徑如圖8所示。
如前述的圖5避障的過程,該算法的避障過程也會使植保無人機的噴施過程產生重噴和漏噴的情況,重噴面積是植保無人機在第二條回飛路徑上回飛噴施造成的,漏噴面積是躲避障礙時無法噴施到造成的,下面就其多障礙情況下產生的重噴漏噴的面積給予計算和推導。
如圖9所示,已知障礙圓Dk的圓心坐標為(Xdi,Ydi),障礙圓模型的半徑Ri,生成的最小轉彎圓的圓心坐標(Xzi,Yzi),最小轉彎半徑都為Rz。障礙圓的中心點偏離原路線的距離為Li,可構建如上圖所示的三角形區域。
由單條路徑推廣到整片區域,需要考慮到路徑之間的轉彎問題,假設植保無人機滿足Rp>=Rz的條件,則轉彎時可以采取以下方法:植保無人機可以通過Dubins路徑生成形如“LCLCL”的曲線,做180°掉頭,直接飛行到下一條噴施路徑,常見的植保無人機噴施半徑大約是4-8米,此時要求植保無人機的最小轉彎半徑應小于此值。其具體的飛行如圖10所示。
對于整片區域,綜合運用以上方法得到的避障路線如圖11所示。
本發明還可有其它多種實施例,在不背離本發明精神及其實質的情況下,本領域技術人員當可根據本發明作出各種相應的改變和變形,但這些相應的改變和變形都應屬于本發明所附的權利要求的保護范圍。
- 還沒有人留言評論。精彩留言會獲得點贊!