基于近似標準展開式的三維輪廓誤差估計方法及裝置與流程

本發明涉及三維輪廓誤差的估計方法及裝置，尤其涉及基于期望輪廓的泰勒展開法對三維輪廓誤差進行估計的方法及裝置。

背景技術：

隨著人類航空航天、交通運輸、3C產業等的發展，越來越多的制造業裝備采用了高性能三維加工技術，如精密加工中用到的三軸數控機床、半導體封裝設備、電火花切割設備等。伺服系統的輪廓誤差是指當前伺服系統運動末端到期望輪廓的最短距離，輪廓誤差控制的目的是控制多軸伺服系統沿著期望的輪廓運動，尤其是減少與運動方向垂直方向上的誤差。但由于目前的檢測技術難以實時的檢測出輪廓誤差，為了進行輪廓誤差的控制，就必須通過軟件算法對輪廓誤差進行估計。

對于簡單的輪廓，如直線和圓形，可以通過初等幾何知識計算得到當前實際位置到直線和圓的距離，從而得到準確的輪廓誤差。對于復雜的自由曲線，尤其是三維自由曲線，輪廓誤差的準確計算非常復雜，難以滿足實時控制的需求，這就需要對輪廓誤差進行估計。常用的輪廓誤差估計方法可以分為三種：基于局部幾何特性的估計方法，基于代數方程的估計方法，基于進給命令的估計方法。

基于局部幾何特性的估計方法目前可以分為兩類，一類是線性逼近輪廓誤差估計方法，另一類是基于圓逼近輪廓誤差估計方法。線性逼近通過在給定點附近選擇一條直線作為期望曲線的逼近，圓逼近則是使用當前給定點處的密切圓來逼近期望輪廓，這樣通過計算當前給定點到逼近直線或圓的距離來估計輪廓誤差。通過局部幾何特性估計的方法，將輪廓誤差估計問題轉換為求當前位置到逼近曲線距離的問題。基于線性逼近和密切圓逼近的輪廓誤差估計方法要求系統的跟蹤誤差較小，對于線性或者曲率較小的輪廓能夠取得良好的輪廓誤差估計效果，但是對于大曲率曲線，尤其是三維輪廓，則估算誤差較大。

中國發明專利《基于直線段逼近節點的數控系統輪廓誤差控制方法》(申請號：201110378980.5)通過當前實際刀位點和用直線段逼近刀心輪廓指令曲線時的逼近節點，計算當前實際刀位點到刀心輪廓指令曲線的最短距離，即輪廓誤差。中國發明專利《基于空間圓弧近似的輪廓誤差實時估計方法》(申請號：201610625829.X)中，提出一種基于空間圓弧近似的輪廓誤差實時估計方法，并基于一階泰勒展法和牛頓迭代法計算輪廓誤差。以上兩個專利所使用的方法即為基于線性逼近和圓逼近計算輪廓誤差的方法。

基于代數方程的估計方法主要有正交全局任務坐標系方法。對于二維輪廓，正交全局坐標系通過在期望曲線的給定點建立一個移動曲線坐標系，無論跟蹤誤差多大，其估算的輪廓誤差都是真實輪廓誤差的一階逼近。對于三維輪廓，由于正交全局坐標系難以保證在三維空間的正交性，所以正交全局坐標系難以應用于三維輪廓誤差估計。

隨著計算機技術的發展，數控系統的數據存儲能力大大提高，可以保存當前給定點前后若干個數據點。基于進給命令的輪廓誤差估計方法是通過比較當前給定點前后若干個點與當前實際位置的距離大小來估計輪廓誤差。基于進給命令的輪廓誤差估計方法計算簡單，同時適用于二維輪廓和三維輪廓，但其效果和插補密度相關，若插補密度較低，則估計效果較差，并且對數控系統計算和存儲能力有一定要求，要想獲得較高的輪廓誤差估計精度，就需要提高數控系統的硬件成本。

中國發明專利《面向參數曲線刀具輪廓的數控系統輪廓誤差控制方法》(專利號：201210045978.0)中通過對參數曲線刀具輪廓進行曲線插補加工的每個采樣周期，根據當前實際刀位點和所跟蹤參數曲線刀具輪廓上的插補點，計算輪廓誤差。其所使用的輪廓誤差估計方法即是基于進給命令的輪廓誤差估計方法。

綜上所述，在不增加數控系統硬件成本的基礎上，針對大曲率、撓率的三維輪廓，需要一種更高精度、實時的三維輪廓誤差估計方法。

技術實現要素：

為了解決現有輪廓誤差估計方法對于三維大曲率、撓率自由曲線輪廓誤差精度下降的問題，滿足系統實時控制的需求，同時不增加伺服系統硬件存儲的成本。本發明提供了一種在不增加系統硬件成本的同時適用于任意三維自由曲線的基于近似標準展開式的三維輪廓誤差估計方法及裝置。

根據本發明的一方面，提供一種基于近似標準展開式的三維輪廓誤差估計方法，包括以下步驟：

S1、將以弧長為參數的三維期望輪廓在當前時刻的給定點進行泰勒展開；

S2、基于三維期望輪廓在當前時刻給定點的曲率、撓率信息，將上述泰勒展開轉換為以Frenet坐標系坐標基為參數的近似標準展開式；

S3、設置當前伺服系統實際位置到近似標準展開式的距離函數，通過數值解的方法實時求解當前三維實際位置到近似標準展開式的距離，并作為估算的三維輪廓誤差。

優選地，在步驟S1中，將以弧長為參數的三維期望輪廓在當前時刻的給定點進行泰勒展開的展開式為：

其中s代表弧長參數，c_d(s)代表以弧長為參數的期望輪廓，

優選地，步驟S2包括：

S21、將泰勒展開式中的c_d(0)的一階導數、二階導數和三階導數分別轉換為以Frenet坐標系坐標基為參數的表達式：

其中t，n和b分別代表Frenet坐標系下的單位切向量、單位法向量和單位副法向量，其中κ和τ分別代表期望三維輪廓在當前給定點處的曲率和撓率，κ'代表期望三維輪廓在當前給定點處曲率的一階導數；

S22、通過忽略切向量和法向量上s³以上的高階無窮小量，獲取近似標準展開式：

優選地，步驟S3包括：

S31、將伺服系統編碼器檢測的末端執行器在Frenet坐標系下的坐標設置為(t_A,n_A,b_A)，且近似標準展開式曲線上距離當前伺服系統末端的最短位置坐標為并使用如下距離函數來表示輪廓誤差：

S32、設置所述距離函數的一階導數為零，二階倒數大于零，可得

使用數值求解方法計算上述一元五次方程的所有實數根，并將代入距離函數得到的距離最短的實數根代入下式，從而獲得輪廓誤差：

根據本發明的另一方面，提供一種基于近似標準展開式的三維輪廓誤差估計裝置，包括：

泰勒展開模塊，其配置為，將以弧長為參數的三維期望輪廓在當前時刻的給定點進行泰勒展開；

坐標轉換模塊，其配置為，基于三維期望輪廓在當前時刻給定點的曲率、撓率信息，將上述泰勒展開轉換為以Frenet坐標系坐標基為參數的近似標準展開式；

求解模塊，其配置為，設置當前伺服系統實際位置到近似標準展開式的距離函數，通過數值解的方法實時求解當前三維實際位置到近似標準展開式的距離，并作為估算的三維輪廓誤差。

優選地，在泰勒展開模塊中，將以弧長為參數的三維期望輪廓在當前時刻的給定點進行泰勒展開的展開式為：

其中s代表弧長參數，c_d(s)代表以弧長為參數的期望輪廓，

優選地，轉換模塊包括：

轉換單元，其配置為，將泰勒展開式中的c_d(0)的一階導數、二階導數和三階導數分別轉換為以Frenet坐標系坐標基為參數的表達式：

其中t，n和b分別代表Frenet坐標系下的單位切向量、單位法向量和單位副法向量，其中κ和τ分別代表期望三維輪廓在當前給定點處的曲率和撓率，κ'代表期望三維輪廓在當前給定點處曲率的一階導數；

近似單元，其配置為，通過忽略切向量和法向量上s³以上的高階無窮小量，獲取近似標準展開式：

優選地，求解模塊包括：

輪廓誤差表示單元，其配置為，將伺服系統編碼器檢測的末端執行器在Frenet坐標系下的坐標設置為(t_A,n_A,b_A)，且近似標準展開式曲線上距離當前伺服系統末端的最短位置坐標為并使用如下距離函數來表示輪廓誤差：

輪廓誤差求解單元，其配置為，通過設置所述距離函數的一階導數為零，二階倒數大于零，得到

并利用數值求解方法計算上述一元五次方程的所有實數根，并將代入距離函數得到的距離最短的實數根代入下式，從而獲得輪廓誤差：

本發明的有益效果是：

在不增加多軸伺服系統硬件成本的基礎上，基于近似標準展開式的三維輪廓誤差估計方法能夠有效的提高三維輪廓誤差的估計精度并能有效的應用于實時控制中。

附圖說明

下面結合附圖和實例對本發明作進一步說明，其中：

附圖1是本發明第一實施例的基于近似標準展開式的三維輪廓誤差估計方法的流程圖；

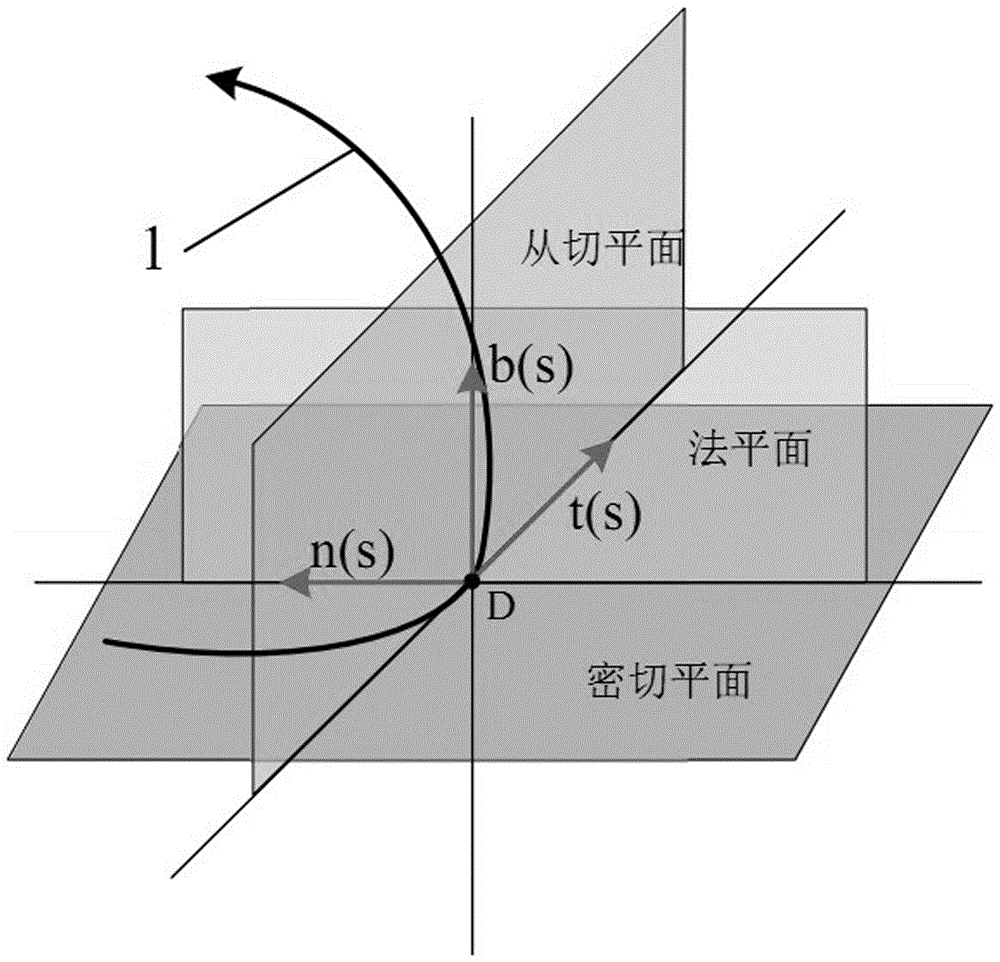
附圖2是三維Frenet標架；

附圖3是基于近似標準展開式的輪廓誤差估計示意圖。

具體實施方式

下面結合附圖說明及具體實施方式對本發明進一步說明。

如圖1所示，根據本發明的第一實施例，提供一種基于近似標準展開式的三維輪廓誤差估計方法，包括以下步驟：

S1、將以弧長為參數的三維期望輪廓在當前時刻的給定點進行泰勒展開；

S2、基于三維期望輪廓在當前時刻給定點的曲率、撓率信息，將上述泰勒展開轉換為以Frenet坐標系坐標基為參數的近似標準展開式；

S3、設置當前伺服系統實際位置到近似標準展開式的距離函數，通過數值解的方法實時求解當前三維實際位置到近似標準展開式的距離，并作為估算的三維輪廓誤差。

根據本發明的優選實施例，步驟S1的具體實現方式如下：

首先以弧長s為參數表示三維期望輪廓c_d(s)，三維期望輪廓在當前時刻的給定位置為點D，設點D處弧長參數為0，即s＝s₀＝0，在s₀附近對c_d(s)進行三階泰勒展開得到：

其中并且

根據本發明的優選實施例，步驟S2的具體實現方式如下：

如圖2所示，在期望曲線1的當前給定點D處可以建立一個Frenet坐標系，在Frenet坐標系下，可以得到c_d(0)的一階導數、二階導數和三階導數的表達式：

其中t，n和b分別代表Frenet坐標系下的單位切向量、單位法向量和單位副法向量，其中κ和τ分別代表期望三維輪廓在當前給定點處的曲率和撓率，κ'代表期望三維輪廓在當前給定點處曲率的一階導數。將(2)式代入(1)式得到以Frenet坐標基的期望曲線表達式：

由于在實際的輪廓控制應用中，弧長s一般較小，可以忽略切向量和法向量上s³以上的高階無窮小量，得到近似標準展開式的表達式：

近似標準展開式的坐標形式寫法為

傳統的線性逼近無曲率、撓率信息，圓逼近只含有曲率信息，而上述近似標準展開式包含三維期望輪廓的曲率和撓率信息，所以能夠有效的提高對于大曲率、撓率的三維曲線的逼近精度。

根據本發明的優選實施例，步驟S3的具體實現方式如下：

如圖3所示，多軸伺服系統末端實際位置A，2為原始給定三維曲線，3為近似標準展開式的曲線，點D為原始給定曲線上在當前時刻的給定點，點E為近似標準展開式的曲線上距離點A最近的位置。

下面計算多軸伺服系統末端實際位置A到上述近似標準展開式的距離，即為估算的輪廓誤差。設由伺服系統編碼器檢測的末端執行器在Frenet坐標系下的坐標為(t_A,n_A,b_A)，近似標準展開式曲線上距離當前伺服系統末端的最短位置坐標為則輪廓誤差可以由下述距離函數表示

輪廓誤差求解問題可以轉換為求解上式距離函數的最小值問題，使L²(A,·)一階導數為零，二階導數大于零的解即為距離函數的最小值解。

最終輪廓誤差的求解轉換為求方程(8)的實數解的問題。方程(8)為一個一階五次方程，由Abel-Ruffini定理知，一階五次方程沒有解析解。本發明通過數值求解的方法解出方程(8)的所有實數根。

通過以上方法得到方程(8)的所有實數解后，代入方程(9)，得到滿足方程(9)的實數解后，再代入以下距離函數中

選擇最小的距離函數值為估算的輪廓誤差，代入得到最小輪廓誤差的實數解到(5)中，即得到近似標準展開式曲線上距離當前實際點A最短距離的點E的坐標。本發明算法經過固高科技(深圳)有限公司生產的商用運動控制器GT400-SV上測試，輪廓控制算法加輪廓誤差估計算法的執行時間在500us以內，能夠滿足實時控制的需求。

根據本發明的第二實施例，提供一種基于近似標準展開式的三維輪廓誤差估計裝置，其特征在于，包括：

泰勒展開模塊，其配置為，將以弧長為參數的三維期望輪廓在當前時刻的給定點進行泰勒展開；

坐標轉換模塊，其配置為，基于三維期望輪廓在當前時刻給定點的曲率、撓率信息，將上述泰勒展開轉換為以Frenet坐標系坐標基為參數的近似標準展開式；

求解模塊，其配置為，設置當前伺服系統實際位置到近似標準展開式的距離函數，通過數值解的方法實時求解當前三維實際位置到近似標準展開式的距離，并作為估算的三維輪廓誤差。

根據本發明的優選實施例，在泰勒展開模塊中，將以弧長為參數的三維期望輪廓在當前時刻的給定點進行泰勒展開的展開式為：

其中s代表弧長參數，c_d(s)代表以弧長為參數的期望輪廓，

根據本發明的優選實施例，轉換模塊包括：

轉換單元，其配置為，將泰勒展開式中的c_d(0)的一階導數、二階導數和三階導數分別轉換為以Frenet坐標系坐標基為參數的表達式：

其中t，n和b分別代表Frenet坐標系下的單位切向量、單位法向量和單位副法向量，其中κ和τ分別代表期望三維輪廓在當前給定點處的曲率和撓率，κ'代表期望三維輪廓在當前給定點處曲率的一階導數；

近似單元，其配置為，通過忽略切向量和法向量上s³以上的高階無窮小量，獲取近似標準展開式：

根據本發明的優選實施例，求解模塊包括：

輪廓誤差表示單元，其配置為，將伺服系統編碼器檢測的末端執行器在Frenet坐標系下的坐標設置為(t_A,n_A,b_A)，且近似標準展開式曲線上距離當前伺服系統末端的最短位置坐標為并使用如下距離函數來表示輪廓誤差：

輪廓誤差求解單元，其配置為，通過設置所述距離函數的一階導數為零，二階倒數大于零，得到

并利用數值求解方法計算上述一元五次方程的所有實數根，并將代入距離函數得到的距離最短的實數根代入下式，從而獲得輪廓誤差：

為了在不增加多軸伺服系統硬件成本的基礎上，提高實時三維自由曲線輪廓誤差估計的精度，本發明專利提出了一種基于近似標準展開式的三維輪廓誤差估計方法。

本發明將三維自由曲線在當前時刻給定點處進行泰勒展開，并整理為以Frenet坐標系為坐標基的形式，根據系統實際運動精度忽略切線方向和法線方向上的弧長s的三階無窮小量，得到了期望曲線的近似標準展開式曲線。然后通過最優化的方法，運用數值求解的方法，得到當前伺服系統末端實際位置到近似標準展開式曲線的距離，即為本發明估算的輪廓誤差。

以上是對本發明的較佳實施進行了具體說明，但本發明創造并不限于所述實施例，熟悉本領域的技術人員在不違背本發明精神的前提下還可作出種種的等同變形或替換，這些等同的變型或替換均包含在本申請權利要求所限定的范圍內。

除非一個必需的步驟需要由前面步驟所產生的輸入，否則本文描述的步驟的特定順序僅用于示例性說明，而非限制。