面向實時控制系統的降低任務延遲的設計方法與流程

本發明屬于嵌入式實時操作系統領域，特別是一種面向實時控制系統的減小任務輸入輸出延遲和采樣延遲的設計方法。

背景技術：

現代的控制系統通常需要在一個處理器平臺上運行多個任務，包括了對延遲敏感的控制任務和對截止期敏感的實時任務。任務的截止期可通過實時調度算法如固定優先級調度和最早截止期優先調度來做出保證。然而多個任務調度引起的輸入輸出延遲和采樣延遲在實時控制系統中卻不可忽視，這些參數在設計階段如果沒有被仔細考慮，會影響控制性能甚至造成控制系統的不穩定性。

為解決多個任務調度造成的延遲、抖動問題，一些實時控制系統的設計方法被提出。Nilsso和Matri等人提出了控制器補償技術來降低系統的延遲和抖動以提升控制性能；Baruah和Shin等人的方法在保證任務集可調度的情況下來最小化任務的相對截止期，但該方法僅能有效減小部分任務的延遲。Crespo等人將控制任務劃分為采樣、計算、控制輸出三個子任務，并限制采樣和控制輸出在任務開始和結束的一段時間內運行，該方法能夠顯著降低任務的輸入輸出抖動，然而卻以增加輸入輸出延遲為代價。Buttazzo等人在實時控制系統中采用完全不可搶占的任務模型，該方法能夠降低任務的輸入輸出延遲和抖動，然而卻存在任務集資源利用率低等問題。

為了降低任務的運行開銷，提高任務最壞執行時間(WCET)的可預測性，多種限制搶占調度算法被提出，如推遲搶占調度(DPS)，固定搶占點調度(FPP)和搶占閾值調度(PTS)。當使用固定搶占點調度時，相較于完全搶占的固定優先級調度，任務集的可調度性能夠提高。但是固定搶占點調度的優點不僅僅局限于此，將該模型應用于控制系統中，特別是當最后不可搶占區域最大時，任務的輸入輸出延遲可以被減小。但是降低任務輸入輸出延遲的同時，卻給高優先級任務帶來更多的阻塞時間，并且一個任務最后一段不可搶占區域的大小可能會影響該任務的采樣延遲。

技術實現要素：

本發明針對現有技術的不足，提出了一種面向實時控制系統的減小任務輸入輸出延遲和采樣延遲的設計方法，重點考慮了固定優先級調度中最后一段不可搶占區域對輸入輸出延遲和采樣延遲造成的影響，設計了降低任務輸入輸出延遲和采樣延遲的方法，得到了在何種情形下可利用固定搶占點調度算法來減小輸入輸出延遲和采樣延遲以提高控制性能。

步驟一：判斷輸入任務集是否在完全可搶占固定優先級調度下可調度。

在一般情形下，固定優先級調度中最后一段搶占區域的大小可能會對該任務下一個實例的采樣延遲造成影響，進而影響任務的最大采樣延遲。故需要找到一個特定情形即完全可搶占調度下可調度的任務集，在該情形下，最后不可搶占區域的大小僅能影響該任務的輸入輸出延遲而不影響其采樣延遲。將在步驟四通過采樣延遲的計算給出找到該情形的辦法。任務集是否在完全可搶占調度下可調度可通過判斷任務最大響應時間與截止期之間的關系得出。

步驟二：計算任務最大不可搶占區域大小。

對于實時控制系統不僅要降低控制任務的輸入輸出延遲和采樣延遲，還需要保證任務的可調度性。而不可搶占區域的大小會對任務的可調度性造成影響，因而需要計算在保證任務可調度性基礎上最大不可搶占區域的大小。不同于劉錚等人、Chi Young Song等人計算最大不可搶占區域的方法，只有對于在完全可搶占固定優先級調度下可調度的任務集，才可通過計算臨界時刻后第一個實例的最大響應時間來計算任務最大不可搶占區域大小。

步驟三：將控制任務最后一段設置為最大的不可搶占區域。

根據對任務的輸入輸出延遲的分析，固定優先級調度中最后一段不可搶占區域越大對應著越小的輸入輸出延遲。可將控制任務的最后一段不可搶占區域設置為最大，該模型為FP-LNPR模型。

步驟四：將非控制任務設置為完全可搶占。

根據對任務的采樣延遲的分析，固定優先級調度中阻塞時間越大對應著越大的采樣延遲。當對非控制任務設置為完全可搶占時，控制任務的采樣延遲將降到最低。

本發明的有益效果：本發明重點考慮了最后一段不可搶占區域對輸入輸出延遲和采樣延遲造成的影響，設計了降低任務輸入輸出延遲和采樣延遲的方法，得到了在何種情形下可利用固定搶占點調度算法來減小輸入輸出延遲和采樣延遲以提高控制系統的控制性能。

附圖說明

圖1：本發明的流程圖；

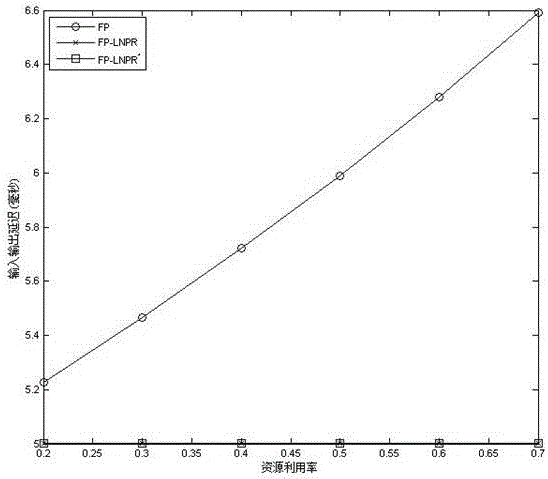
圖2：不同任務模型的輸入輸出延遲比較；

圖3：不同任務模型的采樣延遲比較；

圖4：不同任務模型的控制性能比較。

具體實施方式

以下結合附圖1對本發明作進一步說明。

步驟一：判斷輸入任務集是否在完全可搶占調度下可調度。

輸入的任務集中有n個任務，其中第i個任務由以下參數構成(C_i,D_i,T_i)，分別代表任務的最壞執行時間、截止期和周期。首先需要計算固定優先級調度下第i個任務的響應時間R_i，可通過如下的表達式給出：

由于上述方程的左右兩邊都含有R_i參數，故需要采用以下的迭代方程進行求解:

若該方程收斂，收斂的值即對應著該任務的響應時間R_i。若存在著R_i≤D_i，則該任務為完全可搶占下可調度的任務。對所有的n個任務重復同樣步驟，可判斷該任務集是否是完全可搶占調度下可調度的任務集。

步驟二：計算任務最大不可搶占區域大小

對于一個完全可搶占下可調度的第i個任務來說，采用固定搶占點調度需要滿足以下的條件：

存在著滿足以下的方程：

W_i(t)+α_i≤t(1)

其中為第i個任務最后一段不可搶占區域大小，W_i(t)長為的時間內，第i個任務以及所有高優先級任務所需要運行的時間，可表示為：

公式(1)中的α_i為第i個任務的阻塞時間。

對于方程(1)來說，不需要檢查中的每一個點，僅需要檢查該區間內不可連續的點，如

根據方程(1)，可以得到第i個任務的最大容忍時間β_i，表示為：

β_i＝max{t-W_i(t)}

根據以上可得出第i個任務最大的不可搶占區域大小的計算：

步驟三：將控制任務最后一段設置為最大的不可搶占區域。

基于固定搶占點模型，找出造成最大輸入輸出延遲的時刻并找出最大輸入輸出延遲的計算方法，見圖2。找出最后一段不可搶占區域與輸入輸出延遲的關系，將控制任務最后一段不可搶占區域設置為最大。可分為以下幾個步驟：

(1)計算造成最大輸入輸出延遲時刻。該時刻對應于所有高優先級任務的同步釋放，且該時刻距該任務開始執行僅有一段極小的時間。

(2)計算最大輸入輸出延遲的方法。將最大輸入輸出延遲的計算分為三個部分，即該任務開始運行到造成最大輸入輸出延遲時刻之間的一段極小的時間ε，除最后一段不可搶占區域的所有高優先級任務的響應時間以及最后一段不可搶占區域那么最大輸入輸出延遲可表示為：

其中表示在完全可搶占調度中長為時間內第i個任務的最大占據時間，即任務從開始運行長為的時間到任務重新開始運行一小段時間之間的間隔。

根據最大響應時間與最大占據時間之間的關系式：

可將最大輸入輸出延遲前面兩項簡化為：

則最大輸入輸出延遲表示為：

(3)最大輸入輸出延遲與最后一段不可搶占區域關系。通過比較一個較大的不可搶占區域和一個稍短的不可搶占區域之間的輸入輸出延遲的關系，找到了最后一段不可搶占區域與輸入輸出延遲的關系，即當最后一段不可搶占區域最大時對應著最小的輸入輸出延遲。可通過歸納法給出證明。步驟如下：

a.初始迭代中，一個稍大的不可搶占區域與稍短的不可搶占區域之間的輸入輸出延遲比較。

b.假設第n次迭代，一個稍大的不可搶占區域的輸入輸出延遲要比稍短的不可搶占區域來的小。

c.計算第n+1次迭代，一個稍大的不可搶占區域的輸入輸出延遲與稍短的不可搶占區域的輸入輸出延遲關系。

(4)根據以上最后一段不可搶占區域大小與輸入輸出延遲的關系，可將固定優先級調度的控制任務的最后一段不可搶占區域設置為最大，該模型為FP-LNPR模型。

步驟四：將非控制任務設置為完全可搶占。

基于固定搶占點模型，計算造成最大采樣延遲的時刻，計算在何種情形下采樣延遲不受該任務最后一段不可搶占區域的影響，最后根據采樣延遲與最后不可搶占區域大小的關系，將非控制任務設置為完全可搶占，見圖3。具體步驟如下：

計算何時不存在采樣延遲自推現象，即釋放在上一個實例最后不可搶占區域的高優先級任務不會對該實例的采樣延遲造成影響。通過反證法來證明一個在完全可搶占調度下可調度的任務集不會產生該現象。

計算不存在著采樣延遲自推現象的任務，何種時刻該任務存在著最大的采樣延遲。對于第i個任務，其在第i個任務的臨界時刻后的第一個實例中可找到最大采樣延遲。

對于不存在采樣延遲自推現象的任務集計算最大采樣延遲。可對阻塞時間B_i＝0和阻塞時間B_i>0分別討論：

根據以上計算采樣延遲的方法，對于不存在采樣延遲自推現象的任務集計算阻塞時間與最大采樣延遲的關系，最后不可搶占區域與最大采樣延遲的關系。在固定優先級調度中越長的阻塞時間對應越大的采樣延遲，而不可搶占區域大小不影響該任務的采樣延遲大小，這也是步驟一中篩選掉完全可搶占調度中不可調度任務集的理由。

根據以上采樣延遲和最后一段不可搶占區域關系，將非控制任務設置為完全可搶占，該任務模型為FP-LNPR^*模型，圖4給出了不同任務模型的控制性能比較。