超聲波電機伺服控制系統不對稱滯回補償控制裝置及方法與流程
本發明涉及電機控制器領域,特別是一種超聲波電機伺服控制系統不對稱滯回補償控制裝置及方法。
背景技術:
現有的超聲波電機伺服控制系統的設計中由于速度死區的存在,使得系統的性能受到影響,對周期重復信號控制時有一定的誤差。
為了改善系統的跟隨性能,我們設計了基于速度死區補償的超聲波電機伺服控制系統。從速度跟隨的實作結果中,我們發現系統在速度關系基本是線性,且參數的變動、噪聲、交叉耦合的干擾和摩擦力等因素幾乎無法對于速度輸出造成影響,故基于速度死區補償的超聲波電機伺服控制系統能有效的增進系統的控制效能,并進一步減少系統對于不確定性的影響程度,因此電機的力矩與速度控制可以獲得較好的動態特性。
技術實現要素:
本發明的目的在于提供一種基于速度死區補償的超聲波電機伺服控制系統,該裝置及其控制系統不僅控制準確度高,而且結構簡單、緊湊,使用效果好。
為實現上述目的,本發明的技術方案是:一種超聲波電機伺服控制系統不對稱滯回補償控制裝置,包括控制系統、基座和設于基座上的超聲波電機,其特征在于:所述超聲波電機一側輸出軸與光電編碼器相連接,另一側輸出軸與飛輪慣性負載相連接,所述飛輪慣性負載的輸出軸經聯軸器與力矩傳感器相連接,所述光電編碼器的信號輸出端、所述力矩傳感器的信號輸出端分別接至控制系統;所述控制系統包括一不對稱補償控制器。
進一步的,所述控制系統包括超聲波電機驅動控制電路,所述超聲波電機驅動控制電路包括控制芯片電路和驅動芯片電路,所述光電編碼器的信號輸出端與所述控制芯片電路的相應輸入端相連接,所述控制芯片電路的輸出端與所述驅動芯片電路的相應輸入端相連接,以驅動所述驅動芯片電路,所述驅動芯片電路的驅動頻率調節信號輸出端和驅動半橋電路調節信號輸出端分別與所述超聲波電機的相應輸入端相連接;所述不對稱補償控制器設置于控制芯片電路中。
進一步的,所述聯軸器為一彈性聯軸器。
本發明還提供一種超聲波電機伺服控制系統不對稱滯回補償控制方法,其特征在于,包括以下步驟:建立一不對稱滯回數學模型,在不對稱滯回數學模型的基礎進行不對稱補償控制,從而使得系統力矩速度的特性接近線性關系,通過在減小辨識動態誤差的同時也使得伺服系統滯回最小,具體包括以下步驟:步驟S1:超聲波電機驅動系統的動態方程可以寫為:其中Ap=-B/J,BP=J/Kt>0,CP=-1/J;B為阻尼系數,J為轉動慣量,Kt為電流因子,Tf(v)為摩擦阻力力矩,TL為負載力矩,U(t)是電機的輸出力矩,θr(t)為通過光電編碼器測量得到的位置信號;步驟S2:建立一不對稱滯回模型;步驟S3:輸入信號v(t)先經過逆不對稱系統,其輸出作為控制信號進入不對稱系統,使用不對稱補償控制使得系統力矩速度的特性接近線性關系。
進一步的,步驟S2具體包括以下步驟:步驟S21:所述不對稱滯回模型結合了函數Sr和密度函數p(r)描述遲滯的非線性,v(t)為輸入信號,Φ[v](t)為不對稱滯回系統的輸出信號,r為系統待辨識的初始參數,所述不對稱滯回模型為:
p(r)為密度函數,Sr[v](t)為函數,其定義如下:
Sr[v](t)=s(v(t),Sr[v](ti)),
對于ti<t<ti+1且0≤i≤N-1,
s(v,z)=max(vl-r,min(vr(v)+r,z))
不對稱滯回模型的輸出表示為:
步驟S22:當輸入單調遞增或者單調遞減時,不對稱滯回模型的輸出分別表示為∏+[v](t)和∏-[v](t):
當輸入單調遞增或者單調遞減時,Fr[v](t)的輸出表示為:
因此,式(2.45)表示為:
然后,得到式(2.45)為:
式(2.52)進一步的表示為:
因為包絡函數γl和γr是可逆的,因此式(2.53)表示為:
得到不對稱滯回模型的輸出表示為:
不對稱滯回模型的輸出∏-[v](t)表示為:
然后,將密度函數和Fr[v](t)代入逆不對稱滯回模型的輸出方程,得到方程為:
逆不對稱滯回模型由初始加載曲線得到:
修改后的初始加載曲線不對稱滯回模型表示為:
不對稱滯回模型的密度函數表示為:
不對稱滯回模型表示為:
上述公式表明,不對稱滯回模型由初始加載曲線表示,逆不對稱滯回模型表示為:
其中是逆模型的閾值而表示的是改進的逆初始載荷曲線;
步驟S23:不對稱滯回模型表示為:
該模型(2.63)的逆表示為:
所以,逆不對稱滯回模型表示為:
為了得到逆模型的參數,用下面方程:
當j=1,2,Kn且r0=0時,F[v]等于信號的輸入v:
Fr=0[v]=v (2.67)
當j=0,不對稱滯回模型的輸出為:
∏[v](t)=p(0)v (2.68)
因此,當r0=0時,逆不對稱滯回模型表示為:
∏-1[v](t)=(p(0))-1v (2.69)
改變閾值r,初始加載曲線表示為:
當且僅當p0=p(0)時;
以類似的方式改變初始加載曲線的閾值r,得:
當且僅當時;
逆的閾值是正的,并且與正的閾值相關;
式(2.66)的導數關于閾值表示為:
逆密度函數的權重用不對稱模型表示為:
與現有技術相比,本發明的有益效果為:使用不對稱補償控制的超聲波電機伺服控制器,系統在力矩速度跟蹤效果上有著顯著的改善且參數的變動、噪聲、交叉耦合的干擾和摩擦力等因素幾乎無法對于運動系統效果造成影響,故基于不對稱補償控制的超聲波電機伺服控制系統能有效的增進系統的控制效能,并進一步減少系統對于不確定性的影響程度,提高了控制的準確性,可以獲得較好的動態特性。此外,該裝置設計合理,結構簡單、緊湊,制造成本低,具有很強的實用性和廣闊的應用前景。
附圖說明
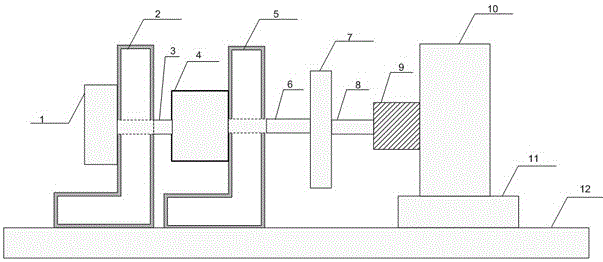
圖1是本發明實施例的結構示意圖。
圖2是本發明實施例的控制電路原理圖。
圖中,1-光電編碼器,2-光電編碼器固定支架,3-超聲波電機輸出軸,4-超聲波電機,5-超聲波電機固定支架,6-超聲波電機輸出軸,7-飛輪慣性負載,8-飛輪慣性負載輸出軸,9-彈性聯軸器,10-力矩傳感器,11-力矩傳感器固定支架,12-基座,13-控制芯片電路,14-驅動芯片電路,15、16、17-光電編碼器輸出的A、B、Z相信號,18、19、20、21-驅動芯片電路產生的驅動頻率調節信號,22-驅動芯片電路產生的驅動半橋電路調節信號,23、24、25、26、27、28-控制芯片電路產生的驅動芯片電路的信號,29-超聲波電機驅動控制電路。
具體實施方式
下面結合附圖和具體實施例對本發明做進一步解釋。
本發明提供一種超聲波電機伺服控制系統不對稱滯回補償控制裝置,如圖1所示,包括基座12和設于基座12上的超聲波電機4,所述超聲波電機4一側輸出軸3與光電編碼器1相連接,另一側輸出軸6與飛輪慣性負載7相連接,所述飛輪慣性負載7的輸出軸8經彈性聯軸器9與力矩傳感器10相連接,所述光電編碼器1的信號輸出端、所述力矩傳感器10的信號輸出端分別接至控制系統。所述控制系統包括一不對稱補償控制器。
上述超聲波電機4、光電編碼器1、力矩傳感器10分別經超聲波電機固定支架5、光電編碼器固定支架2、力矩傳感器固定支架11固定于所述基座12上。
如圖2所示,上述控制系統包括超聲波電機驅動控制電路29,所述超聲波電機驅動控制電路29包括控制芯片電路13和驅動芯片電路14,所述光電編碼器1的信號輸出端與所述控制芯片電路13的相應輸入端相連接,所述控制芯片電路13的輸出端與所述驅動芯片電路14的相應輸入端相連接,以驅動所述驅動芯片電路14,所述驅動芯片電路14的驅動頻率調節信號輸出端和驅動半橋電路調節信號輸出端分別與所述超聲波電機4的相應輸入端相連接。所述驅動芯片電路14產生驅動頻率調節信號和驅動半橋電路調節信號,對超聲波電機輸出A、B兩相PWM的頻率、相位及通斷進行控制。通過開通及關斷PWM波的輸出來控制超聲波電機的啟動和停止運行;通過調節輸出的PWM波的頻率及兩相的相位差來調節電機的最佳運行狀態。所述不對稱補償控制器(圖中未畫出)設置于控制芯片電路中。
本發明還提供一種基于不對稱補償控制的超聲波電機伺服控制方法,由基于不對稱補償控制的超聲波電機伺服控制器和電機來估測未知的滯回特性動態函數。
本發明通過建立一不對稱滯回數學模型,在不對稱滯回數學模型的基礎進行不對稱補償控制,從而使得系統力矩速度的特性接近線性關系,通過在減小辨識動態誤差的同時也使得伺服系統滯回最小,具體包括以下步驟:步驟S1:超聲波電機驅動系統的動態方程可以寫為:其中Ap=-B/J,BP=J/Kt>0,CP=-1/J;B為阻尼系數,J為轉動慣量,Kt為電流因子,Tf(v)為摩擦阻力力矩,TL為負載力矩,U(t)是電機的輸出力矩,θr(t)為通過光電編碼器測量得到的位置信號;步驟S2:建立一不對稱滯回模型;步驟S3:輸入信號v(t)先經過逆不對稱滯回系統,其輸出作為控制信號進入不對稱滯回系統,使用不對稱補償控制使得系統力矩速度的特性接近線性關系。
當電機的負載力矩較大時,電機力矩-速度特性的滯回不對稱,為了減少此現象造成的影響,我們使用不對稱滯回補償控制對其進行控制。
不對稱滯回模型的建模包括以下步驟:
不對稱滯回模型結合了函數Sr和密度函數p(r)描述遲滯的非線性,v(t)為輸入信號,Φ[v](t)為不對稱滯回系統的輸出信號,r為系統待辨識的初始參數。它表示為:
p(r)為密度函數。Sr[v](t)為函數,其定義如下:
Sr[v](t)=s(v(t),Sr[v](ti)),
對于ti<t<ti+1且0≤i≤N-1,
s(v,z)=max(vl-r,min(vr(v)+r,z))
不對稱滯回模型的輸出可以表示為:
當輸入單調遞增或者單調遞減時,不對稱滯回模型的輸出分別可以表示為∏+[v](t)和∏-[v](t):
當輸入單調遞增或者單調遞減時,Fr[v](t)的輸出可表示為:
因此,式(2.45)可以表示為:
然后,可以得到式(2.45)為:
式(2.52)可以進一步的表示為:
因為包絡函數γl和γr是可逆的,因此式(2.53)可以表示為:
因此可以得到不對稱滯回模型的輸出可以表示為:
不對稱滯回模型的輸出∏-[v](t)可以表示為:
然后,將密度函數和Fr[v](t)代入逆不對稱滯回模型的輸出方程,可得到方程為:
逆不對稱滯回模型可由初始加載曲線得到:
修改后的初始加載曲線不對稱滯回模型可以表示為:
不對稱滯回模型的密度函數可以表示為:
不對稱滯回模型可以表示為:
上述公式表明,不對稱滯回模型可以由初始加載曲線表示。逆不對稱滯回模型可以表示為:
其中是逆模型的閾值而表示的是改進的逆初始載荷曲線。
下面討論逆不對稱滯回模型的參數閾值和密度函數的影響。不對稱滯回模型可以表示為:
該模型(2.63)的逆可以表示為:
所以,逆不對稱滯回模型可以表示為:
為了得到逆模型的參數,可以用下面方程:
當j=1,2,Kn且r0=0時,F[v]等于信號的輸入v:
Fr=0[v]=v (2.67)
當j=0,不對稱滯回模型的輸出為:
∏[v](t)=p(0)v (2.68)
因此,當r0=0時,逆不對稱滯回模型可以表示為:
∏-1[v](t)=(p(0))-1v (2.69)
改變閾值r,初始加載曲線可以表示為:
當且僅當p0=p(0)時;
以類似的方式改變初始加載曲線的閾值r,可得:
當且僅當時;
逆的閾值是正的,并且與正的閾值相關。
式(2.66)的導數關于閾值可以表示為:
那么可以得出結論,逆密度函數的權重可以用不對稱滯回模型可以表示為:
當系統工作時,輸入信號v(t)先經過逆不對稱滯回系統,其輸出作為控制信號進入不對稱滯回系統。由穩定性理論可以證明,上述系統是穩定的。
以上是本發明的較佳實施例,凡依本發明技術方案所作的改變,所產生的功能作用未超出本發明技術方案的范圍時,均屬于本發明的保護范圍。
- 還沒有人留言評論。精彩留言會獲得點贊!