基于變換函數和填充函數的智能控制系統優化算法的制作方法

文檔序號：11132817閱讀：554來源：國知局

本發明提出了一種基于變換函數和填充函數的智能控制系統優化算法，其中智能控制系統是多回路反饋控制系統，它使每一個子回路的控制對象為被優化的函數，通過各子回路的反饋和多子回路的分布，實現控制對象優化；變換函數簡化目標函數，從而使其全局最小點與其它局部最小值分離；填充函數具有使智能控制系統從一個局部最優點跳到另一個更小的局部最優點的功能，如此反復若干次可以得到更加精確的全局最優點。

背景技術：

反饋控制系統優化算法的基本思路來源于單回路控制系統的反饋思想，具體的框圖模型如下圖5所示。其中，輸入給定值R一般是一個小于目標函數最小值的常數；從圖5不難看出，反饋控制系統主要通過輸出反饋產生誤差，經過控制器控制被控對象(被優化的函數)，從而實現尋優，即作為控制對象的被優化函數通過反饋和控制器使其輸出越來越小。

在圖5中，f(k)是第k次迭代時目標函數值；控制器采用增量式PID控制策略，單回路反饋控制系統優化算法的迭代公式定義為：

x(k+1)＝x(k)+k_pΔE(k)+k_iE(k)+k_dΔ²E(k) (1)

上式中的k_p，k_i和k_d分別是PID三個自適應調整參數。

該算法對一些復雜的多極值點的函數，有時達到一定的精度后，就很難再找到更好的極值點，或者無法達到目標要求，為此，某個變換函數被用于簡化目標函數(控制對象)使之盡可能地成為簡單的凸函數。當目標函數的值遠離零時，將其值映射到1或-1，而當目標函數的值接近零時，則將其值盡可能映射到零。另外，由于轉換函數在零附近變化非常大，因此，通過函數變換，可以使目標函數的全局最小點與其它靠近零點的局部最小值分離。結合具有被簡化的控制對象的智能控制系統，我們可以得到目標函數的更加精確的全局最小點。

如果函數T(x)滿足以下兩個性質，我們就把它叫做目標函數f(x)的一個函數變換：

1)T(x)(其中x＞0)是一個連續、可導的一維函數并且在(0,1)或(-1,0)上是單調的。

2)|(T(±10)-T(0))|/T(∞)≥98％

注1：性質1保證了變換后的函數T(x)和目標函數f(x)有著相同的全局最優點。性質2是給出T(x)的有效區間。

該算法面臨兩個問題的考驗。第一個問題是：如何判斷當前的極小值點是全局最優值點；第二個問題是：怎樣從當前局部極小點跳出，移向目標函數更小的局部極小值點。

填充函數法是一種能較好的解決陷入局部極小點的方法，通過構造填充函數能有效地跳出局部極小點，找到另一個比它更小的局部極小點。為了更好地理解填充函數，下面給出三個假設。

假設1：函數f(x)的一個包含最小點的連通域B₁，在其內部任意一點x出發，用速降法都收斂于但B₁外面的部分任意點都不能收斂于則B₁叫做f(X)的一個盆域。

假設2：如果是f(x)的最大點，則f(x)包含的谷域是-f(x)的盆域。

假設3：包含局部最小值點的盆域B₂是高于包含局部最小值的盆域B₁當且僅當

如果一個函數P(x,x^*)滿足以下四個條件，則它被稱為是f(x)在局部最小值點的填充函數：

1)是函數P(x,x^*)的一個嚴格的局部最大點。

2)在任意一個高于盆浴B₁的f(x)的盆浴，P(x,x^*)沒有最小點或者鞍點。

3)如果f(x)有一個在局部最小點比盆域B₁小的盆域B₂，則存在一點x′使得P(x,x^*)最小，且它在和x″的連接線上(它是某一個鄰域)。

4)對于屬于Ω域的任意x、y，滿足和當且僅當P(x)≤(＜)P(y)。

技術實現要素：

本發明的目的在于針對已有技術存在的不足，提供一種基于變換函數和填充函數的智能控制系統優化算法，其智能控制系統是多回路反饋控制系統，它使每一個子回路的控制對象為被優化的函數，通過各子回路的反饋和多子回路的分布，實現控制對象優化。因多極值點的優化函數易陷入局部極值點，引入變換函數簡化控制對象，使被優化的函數的全局最小點能夠與其它靠近零點的局部最小值分離。變換函數是單調一維函數，不影響目標函數的極值點的個數。基于被優化的函數構造的填充函數使控制系統跳出當前局部最小點，并能夠在新的位置重新開始尋找比當前最小值更小的局部最小點，從而避免使系統陷入局部最小點。

為達到上述目的，本發明的構思是：智能控制系統采用多回路反饋控制系統，每一個子回路的控制對象為被優化的函數，利用變換函數對控制對象進行T變換，使被優化函數的全局最小點(接近零點的最小值)能夠與其它靠近零點的局部最小值分離，用自適應PID控制器尋找被優化函數的最優值。當被判斷為陷入局部最小值時(即相鄰兩次迭代后的被優化函數值之差很小時)，此時進入填充函數迭代，直到跳出局部最小值并找到一個更小的最小點，在此基礎上繼續用自適應PID控制器尋找系統最優值。

根據上述發明構思，本發明采用下述技術方案：

第一步：對各個參數進行初始化：在可行域內利用隨機分布確定初始點X_n×d的初值，其中n為并行控制系統個數，d為實際自變量的維數，給各個參數局部最小點x_{_best}，全局最小點x_{_allbest}，局部最小值f_{_best}，全局最小值f_{_allbest}，慣性因子w，PID算法的參數k_i，k_p，k_d，[0,2]之間的常數c₁，c₂，隨機數r₁，r₂區間的初值，并確定算法總循環次數MN，進入填充函數子程序的最大次數TT以及填充函數內迭代的最大次數ND,令k＝1,L＝1.m＝1；

第二步：判斷是否結束算法流程：k>MN或L>TT，若是，則輸出目標函數的全局最優值f_{_allbest},程序結束；否則，k＝k+1,g_i(x)＝f_i(x),i＝1,2,3...n；根據下列的式(3)更新自變量X_n×d和T變換后的目標函數n個子系統的值f(X)＝[f₁,f₂...f_n]并判斷向量x是否超出可行域；

第三步：判斷是否進入填充函數:abs(g_i(x)-f_i(x))＜d₁且m≤ND且f_i(x)≥f_allbest，若是，則x(i,k)＝x(i,k)+d₂×(rand(1,1)-0.5)×exp(d₃(k-1)/ND)

x(i,k)＝x(i,k)+d₄×rand(1,1)×exp(d₅(k-1)/ND)×(x(i,k)-x_allbest)/||x(i,k)-x_allbest||進入填充函數，更新f(x)，T變換后的目標函數n個子系統的值f(X)＝[f₁,f₂...f_n],g_i(x)＝f_i(x),i＝1,2,3...n，然后轉回第三步；否則，跳轉至第四步；

第四步：更新x_{_best}，x_{_allbest}，f_{_best}，f_{_allbest}；

第五步：根據式(4)更新相關誤差量E，ΔE，Δ²E。根據式(5)調整慣性因子w，PID算法的參數k_i，k_p，k_d，然后跳轉至第二步。

上述第二步中，對目標函數f(x)進行T變換的具體方法：目標函數f(x)的T變換為這里T變換函數為更新自變量X_n×d的迭代方程式為：

其中x(i,k)表示第i個子系統的第k次迭代向量，k_i，k_p，k_d是PID算法的參數向量，w是慣性因子。r₁，r₂是初值設定區間的隨機數。c₁，c₂是常數，一般取值范圍是[0,2]。x_best(i)是第i個子系統在迭代過程中的最好位置向量，x_allbest是所有系統在迭代過程的最好位置向量。判斷向量x是否超出可行域：x＜s₁或x＞s₂，若是，則超出可行域，x(i,k+1)＝x_{_allbest}(k)，更新f(X)＝[f₁,f₂...f_n]；否則，沒有超出可行域，以此次迭代結果x(i,k+1)更新f(X)＝[f₁,f₂...f_n]，其中k用來累計算法循環次數，g(x)用來保存該次f(x)的值，MN為算法循環次數的最大值；L用來累計進入填充函數子程序的次數，TT允許進入填充函數子程序的最大次數；s₁，s₂為自變量x有效區間的邊界。

上述第三步中，判斷是否進入填充函數，其判斷條件為：abs(g_i(x)-f_i(x))＜d₁且m≤ND且f_i(x)≥f_allbest，m用來累計在填充函數內迭代的次數，ND為在填充函數內迭代的最大次數，d₁為設定進入填充函數子程序時的相鄰兩次f(x)之差的絕對值的最大值。

2.上述第四步中，更新x_{_best}，x_{_allbest}，f_{_best}，f_{_allbest}：若f(i,k+1)＜f_{_best}(i)，則x_{_best}(i)＝x(i,k+1)，f_{_best}(i)＝f(i,k+1)；若f_{_allbest}(k)＞f_{_best}(i,k+1)，則x_{_allbest}(k)＝x_{_best}(i,k+1)，f_{_allbest}(k)＝f_{_best}(i,k+1)否則跳轉至步驟5)。

上述第五步中，相關誤差量E，ΔE，Δ²E的更新公式和參數ω、k_p、k_i和k_d的自適應修正公式如下：

η是一個非常小的正數，R是系統輸入，f(i,k)表示第i個子系統的第k次系統輸出f(x)的值。ΔE(i,k)表示第i個子系統的第k次系統誤差E(i,k)與第k-1次系統誤差E(i,k-1)的差值，Δ²E(i,k)表示第i個子系統的第k次系統誤差E(i,k)和第k-1次系統誤差E(i,k-1)的差值與第i個子系統的第k-1次系統誤差E(i,k-1)和第k-2次系統誤差E(i,k-2)的差值的差值。

本發明中用到的變換函數：從圖7中可清晰看出函數T(x)在原點附近的值變化很大而定義域內遠離原點的區域變化很平緩，這說明通過變換得到的新目標函數在遠離原點的局部最小值被削減，而在原點附近處的全局最小值被放大了，這樣就減小了系統陷入局部最小點的可能性。為了驗證這一點，取一個例子F1，變換函數T(x)處理前后的曲線如圖8～9所示。

本發明提出了一種不帶參數的填充函數并給出證明：

定理1：如果x₁是f(x)的一個已知的局部最小點，則x₁是P(x,x₁)的一個嚴格的局部最大點。證明：設B₁是f(x)在局部最小點x₁的一個s型盆域，即對任意x∈B₁有f(x)≥f(X₁)，則

這表明x₁是P(x,x₁)的一個嚴格的局部最大點。

定理2：令x₁是f(x)的一個已知的局部最小點，如果x∈S₁＝{x|f(x)≥f(X₁),x≠X₁}，則P(x,x₁)在S₁域內無固定點或者最小點。

證明：因為x∈S₁,則當f(x)＞f(X₁)和x≠X₁，有如果d(x)＝(x-x₁)和x≠X₁，則因此d(x)是對于任意x∈S₁，P(x,x₁)的一個速降方向。當f(y)＝f(X₁)，有則對于滿足｜｜x-x₁｜｜＞｜｜y-x₁｜｜和｜｜x₂-x₁｜｜＜｜｜y-x₁||的任意x,x₂∈S₁，有因此，P(x,x₁)在S₁域內無固定點或者最小點。

定理3：令x₁是f(x)的一個已知的局部最小點，對于任意x₂∈Ω,x₂≠x₁，如果f(x₂)≥f(x₁)，則x₂是P(x,x₁)的一個連續點，或者x₂是P(x,x₁)的一個下半連續點。

證明：因為x₁是f(x)的B₁盆域內的一個局部最小點，所以對于任意x∈B₁，有f(x)≥f(x₁)，則因此，P(x,x₁)在x₁點是連續的。如果f(x₂)≠f(x₁)且x₂≠x₁，即f(x₂)＜f(x₁)或f(x₂)＞f(x₁)，則或這樣存在一個鄰域N(x₂,δ),δ＞0使對于任意x∈N(x₂,δ)，即P(x,x₁)在x₂點是連續的。如果f(x₂)＝f(x₁)且x₂≠x₁，則因此x₂是P(x,x₁)的一個下半連續點。

定理4：令x₁是f(x)的一個已知的局部最小點，x₂是滿足f(x₂)＜f(x₁)的另一個與x₁鄰近的局部最小點，則存在一點x'∈S₂＝{x,f(x)＜f(X₁),x∈Ω}使得P(x,x^*)最小，且它在和x″的連接線上(它是某一個鄰域)。

證明：因為x₁是f(x)的一個已知的局部最小點，則存在一個s型盆域B₁，對于任意x∈B₁，使f(x)≥f(x₁)，由此得到

類似地，關于局部最小點x₂，存在s型盆域B₂，對于某些x₃∈B₂，有f(x₂)≤f(x₃)＜f(x₁)，則對于x₃∈B₂，有

因此P(x',x₁)<P(x₃,x₁),另外P(x₁,x₁)＝0,則當x遠離x₁時，有P(x,x₁)＜0。因此，當f(x)≥f(x₁)時，P(x,x₁)減小，否則P(x,x₁)增加。由定理4，則存在一點x'∈S₂＝{x,f(x)＜f(X₁),x∈Ω}使得P(x,x^*)最小，且它在和x″的連接線上(它是某一個鄰域)。

定理5:令x₁是f(x)的一個已知的局部最小點，以及d是滿足d^T(x-X₁)＞0的一個方向，如果f(x)＞f(X₁),則d是P(x,x₁)在x₁點的一個速降方向。

證明：因為f(x)＞f(X₁)和d^T(x-X₁)＞0,則

因此d是P(x,x₁)在x₁點的一個速降方向。

定理6：令x₁是f(x)的一個已知的局部最小點，對于任意x,y∈Ω滿足

f(x)≥f(X₁),f(y)≥f(X₁)及||x-x₁||≥||y-x₁||當且僅當P(x,x₁)≤P(y,x₁)。

證明：因為對于任意x,y∈Ω滿足f(x)≥f(X₁),f(y)≥f(X₁)，則

因為單調遞增的函數，則對于||x-x₁||＞(≥)｜｜y-x₁｜｜，有P(x,x₁)＜(≤)P(y,x₁)或者對于P(x,x₁)＜(≤)P(y,x₁)，有｜｜x-x₁｜｜＞(≥)｜｜y-x₁｜｜。

注釋1：從定理1—6,很容易看出P(x,x₁)是一個填充函數,因為它滿足了填充函數所有的定義,當f(x)≥f(x₁)，P(x,x₁)減少；當f(x)＜f(x₁)，P(x,x₁)增加,如果d是在點滿足d^T(x-X₁)＞0的P(x,x₁)速降方向,那么通過d可以找到滿足f(x)＜f(x₁)的搜索方向。

令是當前局部極小點,是當前迭代點,λ和μ是兩個給定的常數且0＜λ＜μ,是在的搜索方向，使

定理7:令和如果滿足則

這里，Ω是x的可行域。

證明：如果則

注釋2：從定理3，很容易看到,如果是一個滿足的搜索方向,那么當迭代次數達到足夠大時，搜索將達到Ω的邊界或者找到滿足f(x)＜f(X₁)的點。為了實現

和我們選擇也就是

說,因此這里,η＞0。當邊界Ω非常大的時候,η可以選為一個較大的正數,否則η可以選為一個較小的正數。另外,為了避免搜索達到邊界,有必要采用分布性的學習步長,因此η可以選為一個隨機的正數。

從填充函數的定義出發得到基于填充函數算法的思路，首先使用一種局部優化算法得到目標函數f(X)的一個局部極小點然后在處構造一個填充函數F(x)，在處搜索一點x₁，以x₁為出發點用局部優化算法極小化填充函數F(x)，得到一點x₂，有填充函數的性質可知，點x₂一定在比B₁低的盆域內，再從現已取得的極小點x₂為初始點用局部最優化方法極小化目標函數f(X)，得到f(X)的另一個更優的局部極小點交替進行上述過程就會得到目標函數f(X)的局部極小點列利···x*，滿足從而得到目標函數的全局極小值點。

本發明的基于變換函數和填充函數的智能控制系統優化算法與現有技術相比較具有如下顯而易見的突出實質性特點和顯著優點：

1)智能控制系統是多回路反饋控制系統，它使每一個子回路的控制對象為被優化的函數，通過各子回路的反饋和多子回路的分布，實現控制對象優化。

2)通過函數變換簡化了被優化函數，使其在遠離遠點的局部最小值被削減而在原點附近的局部最小值被放大了，從而減小了陷入局部最小點的可能性，很大程度上增大了找到全局最小值的可能性，提高了尋優的精度和速度。

3)當系統陷入了局部最優點時，進入填充函數迭代，使智能控制系統從一個局部最優點跳到另一個更小的局部最優點，如此反復若干次可以得到更加精確的全局最優點。

4)多回路系統并行計算的智能控制系統與函數變換以及填充函數法的結合，既保留了智能控制系統的多系統分布并行計算的優點，又在一定程度上克服了智能控制系統算法容易陷入局部最優點的不足。

附圖說明

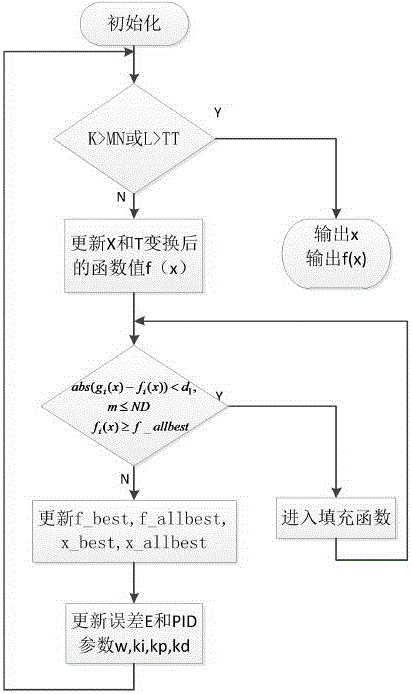
圖1算法主流程圖；

圖2算法子流程圖；

圖3算法子流程圖；

圖4算法子流程圖；

圖5單回路反饋控制系統優化算法的模型

圖6基于變換函數和填充函數的多回路系統框圖；

圖7是變換函數T(x)的曲線；

圖8是F1(x)的曲線，定義域(-6<x<6)；

圖9 T變換后的F1(x)即T(F1(x))的曲線，定義域(-6<x<6)；

圖10對F1基準函數5個算法的仿真曲線；

圖11對F2基準函數5個算法的仿真曲線；

圖12對F3基準函數5個算法的仿真曲線；

圖13對F4基準函數5個算法的仿真曲線；

圖14對F5基準函數5個算法的仿真曲線；

具體實施方式

本發明的優選實施例結合附圖詳述如下：

實施例一：

基準函數：

搜索范圍：-5.12≤x_i≤5.12(本文實驗采用30維)。全局最優值：min(F1)＝F1(0,...,0)＝0。參見圖1～圖9，本基于變換函數和填充函數的智能控制系統優化算法，其特征在于操作步驟如下：

1)對各個參數進行初始化：在可行域內利用隨機分布確定初始點X_5×30＝10.24×(rand(5,30,1)-0.5)，其中5為并行控制系統個數，30為實際自變量的維數，局部最小點x_{_best}＝10.24×(rand(5,30,1)-0.5)，全局最小點x_{_allbest}＝0×rand(1,30,1)，局部最小值f_{_best}＝2×10⁸×rand(5,1,1)，全局最小值f_{_allbest}＝2×10⁷，慣性因子w＝0.01×rand(5,30,1)，PID算法的參數k_i＝k_d＝1×10^-8×rand(5,30,1)，k_p＝5×10^-8×rand(5,30,1)，c₁＝c₂＝1.5，r₁＝r₂＝1.0×(rand(1,1)-0.5)，算法總循環次數MN＝40，進入填充函數子程序的最大次數TT＝80，以及填充函數內迭代的最大次數ND＝300,d₁＝1×10^-15,d₁＝1×10^-7,d₃＝5,d₄＝1,d₅＝3，k＝1，L＝1，m＝1；

2)判斷是否結束算法流程：k>40或L>80，若是，則輸出目標函數的全局最優值f_{_allbest}，程序結束；否則，k＝k+1,g_i(x)＝f_i(x),i＝1,2,3，4,5；更新自變量X_5×30和T變換后的目標函數5個子系統的值f(X)＝[f₁,f₂...f₅]并判斷向量x是否超出可行域；

3)判斷是否進入填充函數：abs(g_i(x)-f_i(x))＜1×10^-15且m≤300且f_i(x)≥f_allbest，若是，則x(i,k)＝x(i,k)+1×10^-7×(rand(1,1)-0.5)×exp(5×(k-1)/300)

x(i,k)＝x(i,k)+1×rand(1,1)×exp(3×(k-1)/300)×(x(i,k)-x_allbest)/||x(i,k)-x_allbest||進入填充函數，更新f(x)，T變換后的目標函數5個子系統的值f(X)＝[f₁,f₂...f₅],g_i(x)＝f_i(x),i＝1,2,3，4,5,然后轉回步驟3)；否則，跳轉至步驟4)；

4)更新x_{_best}，x_{_allbest}，f_{_best}，f_{_allbest}；

5)更新相關誤差量E，ΔE，Δ²E；調整慣性因子w，PID算法的參數k_i，k_p，k_d，然后跳轉至步驟2)。

實施例二：

本實施例與實施例一基本相同，特別之處在于如下：

所述操作步驟2)中，對目標函數f(x)進行T變換的具體方法：目標函數f(x)的T變換為這里T變換函數為更新自變量X_n×d的迭代方程式為：

其中x(i,k)表示第i個子系統的第k次迭代向量，x_best(i)是第i個子系統在迭代過程中的最好位置向量，x_allbest是所有系統在迭代過程的最好位置向量；判斷x(i,k+1)是否超出可行域：x＜-5.12或x＞5.12，若是，則超出可行域，x(i,k+1)＝x_{_allbest}(k)，更新f(X)＝[f₁,f₂...f₅]；否則，沒有超出可行域，以此次迭代結果x(i,k+1)更新f(X)＝[f₁,f₂...f₅]。

所述操作步驟3)判斷是否進入填充函數：判斷條件為abs(g_i(x)-f_i(x))＜1×10^-15且m≤300且f_i(x)≥f_allbest，若是，則x(i,k)＝x(i,k)+1×10^-7×(rand(1,1)-0.5)×exp(5×(k-1)/300)

x(i,k)＝x(i,k)+1×rand(1,1)×exp(3×(k-1)/300)×(x(i,k)-x_allbest)/||x(i,k)-x_allbest||進入填充函數，判斷是否超出可行域，然后更新f(X)＝[f₁,f₂...f₅]，對f(x)進行T變換。

所述操作步驟4)更新x_{_best}，x_{_allbest}，f_{_best}，f_{_allbest}：若f(i,k+1)＜f_{_best}(i)，則x_{_best}(i)＝x(i,k+1)，f_{_best}(i)＝f(i,k+1)；若f_{_allbest}(k)＞f_{_best}(i,k+1)，則x_{_allbest}(k)＝x_{_best}(i,k+1)，f_{_allbest}(k)＝f_{_best}(i,k+1)否則跳轉至步驟5)。

所述操作步驟5)，相關誤差量E，ΔE，Δ²E的更新公式和參數ω、k_p、k_i和k_d的自適應修正公式如下：

這里η＝1×10^-11，系統輸入R＝－20，初始化f(X)＝0×rand(5,1,1)。

實施例三：

圖1為算法主流程圖，首先按圖1對F1進行初始化，然后判斷是否結束算法，若不結束算法按圖2更新自變量X，判斷X是否超出可行域，更新f(x)；然后按圖3判斷是否進入填充函數，判斷X是否超出可行域，更新f(x)，對f(x)進行T變換；然后按圖4更新x_{_best}，x_{_allbest}，f_{_best}，f_{_allbest}；然后按圖1更新相關誤差量E，ΔE，Δ²E的更新公式和參數ω、k_p、k_i和k_d，循環多次上述步驟。以圖5所示經典單回路反饋控制系統為基礎，本發明采用圖6所示基于填充函數的多回路反饋控制系統。圖7為算法中用到的變換函數的圖形。圖8為的圖形，從圖可以看出，F1有很多局部極小點，不便于尋找函數的全局最小點。圖9為對F1變換后的圖形，經變換后全局最優解非常突出，而邊緣的局部極小點被弱化，使全局尋優變得更容易，更精準。

圖10至圖14是以F1～F5為基準函數做出的仿真結果。圖中曲線1為APID算法(參數自適應PID反饋控制系統優化算法)，曲線2為MAPID算法(參數自適應多回路PID反饋控制系統優化算法)，曲線3為TAPID算法(基于變換函數的參數自適應PID反饋控制系統優化算法)，曲線4為TMAPID算法(基于變換函數的參數自適應多回路PID反饋控制系統優化算法)，曲線5為FTMAPID算法(基于變換函數和填充函數的參數自適應多回路PID反饋控制系統優化算法，即本發明論述的算法)。橫坐標為算法迭代次數，縱坐標為f(x)的函數值。從圖10至圖14能看出其中基于變換函數和填充函數的控制系統優化算法收斂的精度能進一步得到提高，收斂的速度也變的更好。

這里對每個測試函數重復實驗30次，統計30次中的最大值(MAX)、最小值(MIN)、成功收斂的平均值(AVG)、置信區間(Confidence Interval，按照95％置信水平)、收斂次數N以及CPU時間(CPU-TIME)。最后為了更直觀地說明問題，在同一幅圖中給出了四個算法的仿真曲線以方便進行性能比較。實驗中允許誤差為SA,即在設定迭代步數內仿真結果與實際最優值之間的誤差小于SA則認為是成功收斂，否則不收斂(用“/”表示)。

表1 F1Generalized Griewanks函數的實驗結果

表2 F2Goldstein-Price函數的實驗結果

表3 F3Shubert函數的實驗結果

表4 F4Shekel’s Family函數的實驗結果

表5 F5weierstrassy函數的實驗結果

從表1至表5的數據可以看出，基于變換函數和填充函數的控制系統優化算法相對于前面四種控制算法，減少了算法陷入最優值的可能，完成了成功收斂且收斂精度都很好。

多系統并行計算的智能控制系統與填充函數法結合的基于變換函數和填充函數的控制系統優化算法，一方面，既保留了智能控制系統的多系統并行計算和群體學習的優點，又在一定程度上克服了智能控制系統算法容易陷入局部最優點的不足。另一方面，智能控制系統算法具有較強的局部搜索能力，而填充函數法則保證了智能控制系統算法的全局搜索，從而大大提高了智能控制系統算法的尋優精度。

下面給出對應于圖10至圖14，作為被優化函數的5個基準測試函數：

1.Generalized Rastrigin函數

函數表達式：

搜索范圍：-5.12≤x_i≤5.12(本文實驗采用30維)。

全局最優值：min(F1)＝F1(0,...,0)＝0。

2.Kowalik函數

函數表達式：

搜索范圍：-2≤x_i≤2(自變量4維)。

全局最優值：min(F2)≈F2(-0.1928,0.1908,0.1231,0.1358)≈3.0749e-4

3.Shubert函數

函數表達式：

搜索范圍：-10≤x_i≤10(自變量2維)。全局最優值：min(F3)＝-186.7309。