基于跨尺度模型的空間機械臂軌跡跟蹤控制方法與流程
本發明屬于智能控制與系統仿真技術領域,尤其是涉及一種基于跨尺度模型的空間機械臂軌跡跟蹤控制方法。
背景技術:
隨著空間技術的不斷發展,太空探索活動進一步延伸。但太空環境具有微重力、高真空、強輻射、大溫差等特點,在這樣危險的環境中,采用空間機械臂協助或代替宇航員來完成大量艱巨危險的任務成為世界各空間大國的一致目標。
與地面機械臂的一個顯著差異是空間機械臂的基座是運動的,是一種十分復雜的多輸入-多輸出的強耦合非線性時變系統,使得空間機械臂的控制問題與地面機械臂相比具有許多新的特點。空間機械臂系統數學模型中的跨尺度特征主要表現在參數與非參數變化的跨尺度。參數的跨尺度特征主要表現在難以精確得到的動力學、運動學參數,如各部分質心位置、轉動慣量、負載質量等,同時,還有很多低階時變參數,如隨著燃料消耗基座質量的變化等。非參數的跨尺度特征無法用定常參數描述,如機械臂低速運動時的非線性摩擦力、結構共振和一些高階未建模誤差等。一些針對地面機械臂能夠達到較好效果的控制方法,未必適用于空間機械臂。針對軌跡跟蹤控制問題,目前常用的控制方法主要有PID控制、自適應控制、魯棒控制和智能控制。
Parlaktuna和Ozkan將漂浮基空間機械臂的控制問題由慣性空間轉化到關節空間內,在得到空間機械臂系統參數線性化的動力學方程后,設計了一種關節空間內漂浮基空間機械臂軌跡跟蹤的PD控制方法[1]。但是PID控制屬于線性控制方法,忽略了空間機械臂系統中的非線性因素和外界干擾,同時,PID控制 往往需要較大的控制能量,不適用于跟蹤精度要求較高的情況。所以當空間機械臂系統存在參數或非參數跨尺度特征時,控制效果并不理想。
Wang H和Xie Y針對漂浮基空間機械臂設計了一種遞推自適應控制方法,利用參數自適應律實時估計控制參數[2];梁捷、陳力設計了一種標稱計算力矩控制附加自適應模糊補償控制的復合控制方法,能夠有效地克服空間機械臂系統未知參數的影響[3];張福海等設計了一種笛卡兒空間內的自適應軌跡跟蹤控制方法,在保證慣量矩陣可逆的同時,又可以實時估計控制參數[4]。然而上述自適應控制方法僅有效地克服了參數變化對空間機械臂系統的影響,當漂浮基空間機械臂系統存在外部擾動等非參數的跨尺度特征時,單純地采用自適應控制方法難以保證空間機械臂系統的穩定性,需要與其它先進的控制策略相結合提高空間機械臂系統魯棒性。
謝立敏等針對空間機械臂關節控制輸入力矩幅值受限且空間機械臂系統存在不確定參數的復雜情況,設計了一種魯棒自適應混合控制方法,對參數進行魯棒自適應調節[5];Pazelli等針對存在參數變化影響和外部干擾的漂浮基空間機械臂系統,對各類非線性H∞控制方法進行研究分析[6]。然而上述魯棒控制方法是以先驗知識上界為基礎設計的,是一種比較保守的控制策略,因此不是最佳控制。
郭益深和陳力利用徑向基神經網絡,提出了一種無需機械臂動力學模型的自適應神經網絡控制方法[7],但并沒有討論模型存在跨尺度特征時的解決方法;謝箭等提出了一種針對漂浮基空間機械臂的神經網絡自適應控制方法,通過徑向基神經網絡逼近模型的非線性函數和不確定性上界,提出的自適應控制律保證了權值的有界性[8],但是所設計的自適應律較為復雜,影響計算速度;張文輝等設計了一種徑向基神經網絡魯棒自適應控制方法,應用于漂浮基空間機械臂 系統[9],雷霆針對控制力矩受限的漂浮基空間機械臂系統,設計了一種神經網絡自適應控制方法[10],然而這兩種方法針對參數變化所設計的補償律包含了動力學模型的全部信息,其中模型的標稱部分為已知信息,在補償律中屬于冗余部分。
技術實現要素:
本發明的目的是提供一種神經網絡自適應控制方法,針對動力學模型中具有參數及非參數跨尺度的空間機械臂系統,實現關節空間對期望軌跡的快速精確跟蹤。
為實現上述目的,本發明提供一種基于跨尺度模型的空間機械臂軌跡跟蹤控制方法,其特征在于:設計神經網絡自適應控制律,將空間機械臂系統動力學模型中存在跨尺度特征的變化項表示為利用神經網絡對變化項f進行逼近,從而實現對變化項f的補償,神經網絡控制律為 v為用于克服神經網絡逼近誤差的魯棒項,其值為v=Kv sgn(r);誤差函數為神經網絡的形式為徑向基神經網絡,徑向基神經網絡的輸入取理想的逼近算法為 則網絡的輸出為徑向基神經網絡權值調整自適應律為D0、C0為對象的名義模型,D0=D-ΔD,C0=C-ΔC,ΔD、ΔC為建模誤差矩陣,d是總和擾動,e=qd-q和分別為關節角跟蹤誤差和角速度跟蹤誤差,qd和q分別為期望和實際的關節矢量,KP、KI分別是正定比例和積分增益矩陣,Kv為魯棒項系數,為神經網絡的權值向量,為高斯基函數的輸出向量,ci為網絡第i個節點的中心矢量,bi為節點i的基寬度參數。
與現有技術相比本發明的有益效果是:
考慮到空間機械臂系統中的建模誤差和外界干擾,用徑向基神經網絡對空間機械臂系統動力學模型中存在跨尺度特征的參數及非參數項f進行在線逼近,f僅包括建模誤差ΔD(q)、以及未知干擾無需考慮已知的標稱模型。利用神經網絡的學習能力,有效抑制了參數與非參數跨尺度變化對空間機械臂系統的影響,自適應律可在線調整神經網絡權值,保證了權值的有界性,解決了未知上界有界的問題。
本發明仿真結果得出,在2s內,關節1和關節2的角位移、角速度迅速跟蹤上期望軌跡。關節角跟蹤誤差穩定在±5×10-3rad以內,關節角速度誤差穩定在±5×10-3rad/s以內,實現空間機械臂關節空間內對期望軌跡的快速精確跟蹤。
附圖說明
圖1是平面2連桿空間機械臂模型圖;
圖2是神經網絡自適應控制方法結構框圖;
圖3是關節1角度跟蹤隨時間變化的曲線;
圖4是關節2角度跟蹤隨時間變化的曲線;
圖5是關節1角速度跟蹤隨時間變化的曲線;
圖6是關節2角速度跟蹤隨時間變化的曲線;
圖7是關節1關節角跟蹤誤差隨時間變化的曲線;
圖8是關節2關節角跟蹤誤差隨時間變化的曲線;
圖9是關節1關節角速度跟蹤誤差隨時間變化的曲線;
圖10是關節2關節角速度跟蹤誤差隨時間變化的曲線;
圖11是關節1的控制力矩隨時間變化的曲線;
圖12是關節2的控制力矩隨時間變化的曲線;
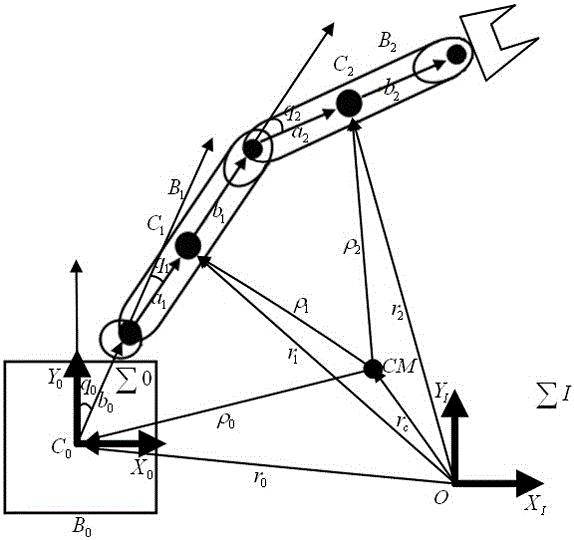
其中:∑I,慣性坐標系;∑0,運動基座坐標系;O,慣性坐標系原點;CM,空間機械臂系統總質心;Bi,剛體i,機械臂的第i個連桿;B0,運動基座,連桿0;Ci,連桿i的質心;C0,基座的質心;ri∈R2,連桿i質心的位置矢量;r0,基座質心的位置矢量;rc∈R2,空間機械臂系統質心CM的位置矢量;pi∈R2,連桿i的位置矢量;ai,從關節Ji到連桿i質心的矢量;bi,從連桿i質心到關節Ji+1的矢量;b0,從基座質心到關節J1的矢量。
具體實施方式
平面2連桿空間機械臂模型如圖1,由可自由漂浮的運動基座B0和兩個臂桿B1、B2組成。
空間機械臂系統各項動力學參數如表1所描述,由基座的初始位置和姿態角和連桿1、連桿2的初始姿態角組成的矢量為[qb,qs]T=[x,y,q0,q1,q2]T,基座和連桿1、連桿2的初始速度矢量為各項參數及期望軌跡的初始數值如表2所示。
表1 平面2連桿空間機械臂系統參數表
表2 空間機械臂神經網絡自適應控制仿真初始值
設置控制參數為KP=diag{100,100,100,100,100},KI=diag{250,250,250,250,250}, Kv=0.2,FW=diag{0.0005,0.0005,0.0005,0.0005,0.0005},根據圖2的控制方法結構框圖進行仿真驗證,本發明以平面2連桿漂浮基空間機械臂系統為研究對象,動力學方程為
其中,q=[q1 q2]T為關節角位移量,D(q)5×5為空間機械臂的慣性矩陣,表示包括非線性離心力和哥氏力的矩陣,τ為控制力矩。
空間機械臂的動力學方程滿足如下性質:
性質1 慣性矩陣D(q)是對稱、正定、有界矩陣。
性質2 選擇適當的可使D(q)和滿足
性質3 存在kc>0及正定函數使得
性質4給定誤差矩陣滿足ΔDl≤||ΔD||≤ΔDh,ΔCl≤||ΔC||≤ΔCh,其中h和l分別為上下界值。
為了實現關節空間內對期望軌跡的快速精確跟蹤,建模時還需考慮空間機械臂系統存在參數與非參數跨尺度特征。引入外部擾動,可以將動力學方程式改寫為如下形式
其中,是總和擾動,包括摩擦力矩擾動和其他外部擾動。
在實際工程中,對象的實際模型很難得到,即無法得到精確的D(q)、只能建立理想的名義模型。將動力學方程寫成理想模型和存在跨尺度特征的變化項之和的形式,則可以表示為
其中,D0、C0為對象的名義模型,D0(q)=D(q)-ΔD(q),ΔD(q)、為誤差矩陣,為包括建模誤差 和外部干擾力矩等存在跨尺度特征的參數與非參數項,為一未知非線性時變函數,具體形式為
由于D(q)是可逆的,可得
設計誤差函數為
其中,e=qd-q和分別為關節角跟蹤誤差和加速度跟蹤誤差,qd和q分別為期望和實際的關節矢量,KP、KI分別是正定比例和積分增益矩陣。
求導可得
令導出等效控制律
因此得到穩定的閉環系統為
針對名義模型,控制律設計為
考慮到未知干擾,可以得出
得
由此可見,模型中存在跨尺度特征的變化項為
采用徑向基神經網絡逼近f,網絡輸入取則網絡輸出為
則
設計控制律為
其中,v=Kv sgn(r)為魯棒項,用于克服神經網絡逼近誤差造成的影響。
定義Lyapunov函數為
其中,D和FW為正定陣,即則V是正定的。
求導,并結合性質2可得
整理可得
根據條件考慮到v=Kv sgn(r),可得
取則可設計如下自適應律以調整徑向基神經網絡的權值
于是可得
為了方便描述,定義
于是
由性質3和性質4可取KvIn>|Q|,其中In=[1,1,…,1]T∈Rn,則
控制結構的輸入為關節角的期望軌跡,輸出關節角的實際值作為負反饋與關節角的實際值作比較,根據關節角的跟蹤誤差、誤差函數和魯棒項設計神經網絡自適應控制系統,仿真結果如圖3-圖12所示。
關節1和關節2的角度隨時間變化曲線如圖3、圖4,角速度隨時間變化曲線如圖5、圖6。其中的紅色虛線表示軌跡跟蹤的期望值,藍色實線表示實際的關節矢量。可以看出,關節1和關節2的角位移、角速度在2s內迅速跟蹤上期望軌跡。
關節1和關節2的角度跟蹤誤差隨時間變化曲線如圖7、圖8,可以看出,關節角跟蹤誤差保持在±5×10-3rad范圍內。
關節1和關節2的角速度跟蹤誤差隨時間變化曲線如圖9、圖10,可以看出,關節角速度跟蹤誤差保持在±5×10-3rad/s范圍內。
關節1和關節2的控制力矩隨時間變化曲線如圖11、圖12,可以看出,各關節控制力矩保持在可實現的范圍內。
運動基座的位置及姿態角隨時間變化的曲線,可以看出,連桿1和連桿2的運動造成基座位置和姿態的變化較為平緩,適用于漂浮基空間機械臂的軌跡跟蹤控制。
實驗結果驗證了神經網絡自適應控制算法的有效性,對于動力學模型中存在參數與非參數跨尺度特征的情況,能夠快速地在線跟蹤期望軌跡,具有一定的魯棒性和抗干擾性。
- 還沒有人留言評論。精彩留言會獲得點贊!