一種非均勻噪聲下窄帶近場信號源定位方法與流程

本發明屬于陣列信號處理技術領域，具體涉及一種非均勻噪聲下窄帶近場信號源定位方法。

背景技術：

近場信源定位技術在使用麥克風陣列的說話人定位系統、家用輔助導航系統、雷達、聲納、無線通信和地質勘探等領域具有重要的應用。已經有很多用于解決近場信號源定位問題的方法被提出，如加權線性預測方法(wlp)和基于esprit的近場定位(n-gesprit)方法等。然而，這些方法大多是基于均勻白噪聲假設的，即假設陣列噪聲是未知的均勻白噪聲或者很容易轉化為均勻白噪聲的已知統計特性的任意噪聲。顯然，在實際應用中，均勻噪聲的假設并不總是成立的。為適應更一般的應用，通常將噪聲模型建立為非均勻白噪聲。在該噪聲模型下，前述算法的性能會受到很大影響，估計精度大大降低。

技術實現要素：

本發明的目的在于克服現有技術中存在的問題，提供一種非均勻噪聲下窄帶近場信號源定位方法，能夠適用于非均勻噪聲模型，估計精度高。

為了達到上述目的，本發明采用如下技術方案：

包括以下步驟：

(1)利用對稱均勻線陣的陣列輸出信號求得接收數據陣列協方差矩陣的估計值

(2)利用接收數據陣列協方差矩陣的估計值的主反對角線元素消除距離未知量，并構造出托普利茲結構矩陣將非均勻噪聲轉化為均勻噪聲；

(3)在構造的托普利茲矩陣上使用波達方向估計方法獲得窄帶近場信號源方向的估計值

(4)利用接收數據協方差矩陣的估計值的第二反對角線元素和窄帶近場信號源方向的估計值構造出僅含有距離未知量的托普利茲結構矩陣

(5)使用托普利茲結構矩陣獲得窄帶近場信號源距離的估計值

其中，窄帶近場信號為入射到對稱均勻線陣上的k個非相干信號對稱均勻線陣包含2m+1個全向傳感器陣元，m的取值范圍為m≥k，陣元間距為d，窄帶近場信號的方位信息為θk表示第k個非相干信號sk(n)的波達方向角，波達方向角為第k個非相干信號sk(n)相對于對稱均勻線陣法向的逆時針夾角，rk是第k個非相干信號sk(n)相對于對稱均勻線陣的中心的距離。

進一步地，步驟(1)中獲取接收數據陣列協方差矩陣的估計值具體包括以下步驟：

101、令對稱均勻線陣的中心為參考陣元，陣列輸出信號為

y(n)＝a(θ,r)s(n)+w(n)(1)

其中，α是陣列響應矩陣，a是導向矢量，定義為(·)^t表示轉置，τmk表示第k個窄帶近場信號在第m個傳感器上由于時間延遲而引起的相位延遲，j表示單位虛數，j²＝-1；

當第k個窄帶近場信號在菲涅耳區時，將τmk用泰勒級數展開：

其中，λ是窄帶近場信號波長，d是陣元間距，o()表示一階無窮小；

陣列噪聲w(n)為時空不相關的零均值高斯隨機過程，并且與接收信號不相關，則：

其中q表示噪聲協方差矩陣，定義為：其中，表示第m個陣元上的噪聲功率；

102、根據陣列輸出信號求得接收數據陣列協方差矩陣r：

r＝e{y(n)y^h(n)}(4)

103、實際應用中由于有限采樣，采用接收數據陣列協方差矩陣的估計值來近似替代r，其計算方式為：

其中，n表示采樣數。

進一步地，步驟(2)中托普利茲結構矩陣的具體構造步驟包括：

201、根據接收數據陣列協方差矩陣r的定義將其展開，r的第(p,q)個元素為：

其中，pk表示第k個窄帶近場信號源的功率，a(θk,rk)表示第k個窄帶近場信號源對應的導向矢量，q表示噪聲協方差矩陣，只含有方向信息，含有方向信息和距離信息；

202、令φk的系數(p-m-1)²-(q-m-1)²等于零，消除距離未知量rk，得到p,q的關系為：q＝2m+2-p，選擇接收數據陣列協方差矩陣的估計值中滿足這一關系的主反對角線元素：

其中，δs,t表示克羅內克函數；

203、構造托普利茲結構矩陣

進一步地，步驟(3)中，經過代數推導，將托普利茲結構矩陣化為：其中a1(θ)定義為表示信源協方差矩陣，im+1表示(m+1)×(m+1)維的單位矩陣；對進行奇異值分解，利用經典波達方向估計方法估計出信源方向的估計值

進一步地，經典波達方向估計方法采用music算法。

進一步地，步驟(4)中，構造托普利茲結構矩陣的具體步驟包括：

301、根據接收數據陣列協方差矩陣r的定義將其展開，r的第(p,q)個元素為：

其中，pk表示第k個窄帶近場信號源的功率，a(θk,rk)表示第k個窄帶近場信號源對應的導向矢量，q表示噪聲協方差矩陣，只含有方向信息，含有方向信息和距離信息；

302、令q＝2m-p，選擇接收數據陣列協方差矩陣的估計值中滿足這一關系的第二反對角線元素：

其中，δs,t表示克羅內克函數，

303、構造托普利茲結構矩陣

進一步地，獲得窄帶近場信號源距離的估計值的具體步驟包括：

經過代數推導，將得到的化為：其中a2(θ,r)定義為im表示m×m維的單位矩陣；由于步驟(3)中已經得到窄帶近場信號源方向的估計值，則中只含有距離未知量，對進行奇異值分解，利用波達方向估計的方法得到窄帶近場信號源距離的估計值

與現有技術相比，本發明具有以下有益的技術效果：

本發明對非均勻噪聲下近場信號源進行定位，利用接收數據陣列協方差矩陣的主反對角線元素構造出托普利茲結構矩陣，消除了方向未知量并且將非均勻噪聲轉化為了均勻噪聲，先估計得到信號的波達方向角，再利用波達方向的估計值和接收數據陣列協方差矩陣的第二反對角線元素構造僅含有距離未知量的托普利茲結構矩陣，估計出信源的距離信息。本發明有效解決了近場信源定位時噪聲非均勻的問題，并且計算簡單。相比于已有的近場信源定位算法，本發明在低信噪比的情況下估計精度明顯優于wpl以及n-gesprit算法，在波達方向和距離上都有良好的估計性能，本發明簡單有效并且適用于更一般的噪聲場景，應用范圍更廣。

附圖說明

圖1為本發明陣列結構圖。

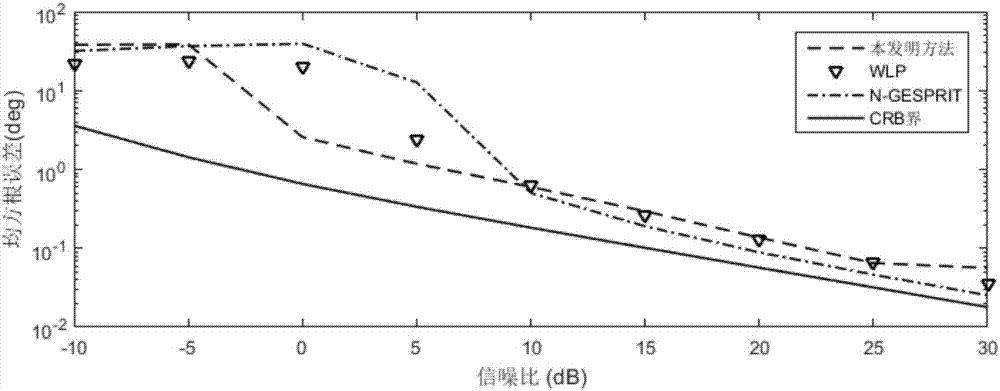
圖2(a)為近場信號波達方向角參數的估計性能隨信噪比(snr)的變化曲線，圖2(b)是近場信號距離參數的估計性能隨信噪比的變化曲線。

圖3(a)為近場信號波達方向角參數的估計性能隨采樣數(n)的變化曲線，圖3(b)為近場信號距離參數的估計性能隨采樣數的變化曲線。

具體實施方式

下面結合附圖對本發明做進一步詳細說明。

本發明中，首先，利用接收數據的陣列協方差矩陣的主反對角線元素消除距離未知量，并構造出托普利茲結構矩陣，將非均勻噪聲轉化為均勻噪聲；然后，在構造的托普利茲矩陣上使用經典的波達方向估計方法估計出信源方向信息；最后，利用接收數據的陣列協方差矩陣的第二反對角線元素和波達方向的估計值構造出僅含有距離未知量的托普利茲結構矩陣，并采用和波達方向類似的方法對信號距離信息進行估計。窄帶近場信號為入射到對稱均勻線陣上的k個非相干信號對稱均勻線陣包含2m+1個全向傳感器陣元，m的取值范圍為m≥k，陣元間距為d，窄帶近場信號的方位信息為θk表示第k個非相干信號sk(n)的波達方向角，波達方向角為第k個非相干信號sk(n)相對于對稱均勻線陣法向的逆時針夾角，rk是第k個非相干信號sk(n)相對于對稱均勻線陣的中心的距離。

下文中，對于任意變量a，表示該變量a的估計值。

一種非均勻噪聲下窄帶近場信號源定位方法，具體實現步驟概括如下：

1)計算接收數據陣列協方差矩陣r的估計值

2)使用的主反對角線元素構造只含有信源方向信息的托普利茲結構矩陣

3)使用估計出信源方向

4)使用的第二反對角線元素構造托普利茲結構矩陣

5)使用估計出信源距離

下面進行具體描述。

k個非相干信號入射到對稱均勻線陣上，該對稱均勻線陣包含2m+1個全向傳感器陣元，m的取值范圍為m≥k，陣元間距為d，窄帶近場信號的方位信息為θk表示第k個非相干信號sk(n)相對于對稱均勻線陣法向的逆時針夾角(波達方向角)，rk是第k個非相干信號sk(n)相對于對稱均勻線陣的中心的距離。參見圖1。

令對稱均勻線陣的中心為參考陣元，陣列輸出信號為

y(n)＝a(θ,r)s(n)+w(n)(1)

其中，α是陣列響應矩陣，a是導向矢量，定義為(·)^t表示轉置，τmk表示第k個信號在第m個傳感器上由于時間延遲而引起的相位延遲，j表示單位虛數，j²＝-1。當第k個信號在菲涅耳區(即rk∈(0.62(d³/λ)^1/2,2d²/λ)，其中d表示陣列孔徑)時，可以將τmk用泰勒(taylor)級數展開：

其中，λ是窄帶近場信號波長，d是陣元間距，o()表示一階無窮小。

w(n)為陣列噪聲，陣列噪聲為時空不相關的零均值高斯隨機過程，并且與接收信號不相關，即：

其中q表示噪聲協方差矩陣，定義為：其中，表示第m個陣元上的噪聲功率。

步驟1)計算接收數據陣列協方差矩陣估計值的具體方法為：

根據真實的陣列輸出信號求得接收數據陣列協方差矩陣r：

r＝e{y(n)y^h(n)}(4)

其中，y(n)表示陣列輸出信號。實際應用中由于有限采樣，無法直接根據(4)式求得接收數據陣列協方差矩陣r，采用估計值來近似替代r，其計算方式為：

其中，n表示采樣數，y(n)表示陣列輸出信號。

步驟2)使用的主反對角線元素構造只含有信源方向信息的托普利茲結構矩陣具體方法為：

a、根據接收數據陣列協方差矩陣r的定義將其展開，r的第(p,q)個元素(第p行第q列對應的元素)為：

其中，pk表示第k個信源的功率，a(θk,rk)表示第k個信源對應的導向矢量，q表示噪聲協方差矩陣，只含有方向信息，含有方向信息和距離信息，λ是入射信號波長，d是陣元間距；

b、令φk的系數(p-m-1)²-(q-m-1)²等于零，從而消除了距離未知量rk。得到p,q的關系為：q＝2m+2-p，選擇接收數據陣列協方差矩陣估計值中滿足這一關系的元素(即主反對角線元素)：

其中，δs,t表示克羅內克函數；

c、構造托普利茲結構矩陣

步驟3)使用估計出信源方向具體方法為：

經過代數推導，可以將(8)中得到的化為：其中a1(θ)定義為表示信源協方差矩陣，im+1表示(m+1)×(m+1)維的單位矩陣。可以看出，此時非均勻噪聲已經轉化為均勻噪聲，且中只含有方向未知量，因此，對進行奇異值分解，利用經典波達方向估計方法(如music算法)便可得到信源方向的估計值

步驟4)使用的第二反對角線元素構造托普利茲結構矩陣的具體方法為：

a、根據接收數據陣列協方差矩陣r的定義將其展開，r的第(p,q)個元素(第p行第q列對應的元素)為：

其中，pk表示第k個信源的功率，a(θk,rk)表示第k個信源對應的導向矢量，q表示噪聲協方差矩陣，只含有方向信息，含有方向信息和距離信息；

b、令q＝2m-p，選擇接收數據陣列協方差矩陣估計值中滿足這一關系的元素(即第二反對角線元素)：

其中，δs,t表示克羅內克函數，

c、構造托普利茲結構矩陣

步驟5)使用估計出信源距離的具體方法為：

經過代數推導，可以將公式(11)中得到的化為：其中a2(θ,r)定義為im表示m×m維的單位矩陣。由于步驟3)中已經得到信源方向估計值，故中只含有距離未知量，因此，對進行奇異值分解，利用類似于波達方向估計的方法(如music算法等)便可得到信源距離的估計值

下面通過以下不同情形對上述方法的效果進行說明：

空間有兩個波達方向角未知的入射信號(即窄帶近場信號)，其方位信息分別為(-13°,1.7λ)，(28°,2.5λ)，對稱均勻線陣含有2m+1＝9個陣元，陣元間隔為d＝λ/4。仿真中對比了本發明和加權線性預測(wpl)以及基于esprit的近場定位(n-gesprit)算法，同時給出了crb界，參見圖2(a)和圖2(b)以及圖3(a)和圖3(b)。另外，信噪比(snr)計算公式為：

式中，pk表示第k個信源的功率，表示第m個陣元上的噪聲功率。每一個仿真結果都是經由p＝1000次獨立重復實驗得到的。陣列噪聲模型為非均勻的時空不相關的零均值高斯噪聲，噪聲協方差矩陣為：

q＝diag{2,20,5,1,0.5,3.7,3,7,18}

由圖2(a)和圖2(b)可以看到，本發明在低信噪比的情況下估計精度明顯優于wpl以及n-gesprit算法。同時本發明計算簡單并且適用于更一般的噪聲場景，應用范圍更廣。在信噪比很高時，本發明方法存在飽和特性，估計精度提升趨于平穩，但這種情況在實際應用中基本不會遇到，故不影響本發明的應用和推廣。

由圖3(a)和圖3(b)可以看到，本發明算法在波達方向角和距離上都有良好的估計性能。