一種短弧段低軌導航衛星實時精密定軌方法與流程

本發明屬于衛星導航技術領域，具體涉及一種短弧段低軌導航衛星實時精密定軌方法。

背景技術：

低軌衛星和微小衛星以其低廉的發射和制造成本，獲得了越來越多的青睞。低軌衛星在通信、遙感、資源管理以及空間基準維持等方面做出了巨大的貢獻，其應用也從傳統的對地觀測擴展到導航領域，因而越來越多的低軌衛星發射計劃被提上日程。著名的銥星計劃通過66顆低軌衛星完成了基于低軌衛星的全球衛星通信系統的組網，并于2016年宣布其衛星授時和位置服務(stl)的計劃，宣告導航衛星進入了低軌衛星時代。國內方面，武漢大學正在研制的低軌衛星珞珈一號搭載了天基導航載荷，也開始了低軌導航衛星的探索性研究。

實時獲取精確的衛星軌道是實現精密衛星導航定位的關鍵技術。目前低軌衛星軌道確定方法主要包括三種：地面監測站定軌、星上自主定軌和事后精密定軌。目前gnss系統，包括gps，glonass，bds等都使用少數的地面跟蹤站實現軌道全弧段觀測，然后計算和預報衛星軌道，上注到導航衛星。該方法對中高軌衛星較理想，但是低軌衛星軌道低，地面可見區域小，要實現全弧段跟蹤通常需要全球均勻分布的數十個甚至上百個跟蹤站，受地理條件限制，難以實現。星上自主定軌是依靠星上的gnss接收機或慣性測量單元進行軌道確定，其中基于gnss觀測值的星上自主定軌方法能夠提供實時，自主連續的leo軌道，因而應用最廣泛。然而受gnss導航衛星廣播星歷的軌道誤差和鐘差的影響，基于gnss觀測值的leo星上自主定軌通常只能獲得數米量級的定軌精度。事后精密定軌是利用低軌衛星下傳的星載gnss觀測數據和精密的gnss軌道和鐘差信息在地面求解leo的精密軌道，也可以加入地面激光測衛(slr)的數據聯合解算。后處理leo精密定軌精度可達2-5cm，但是由于星上觀測數據下傳窗口有限，難以做到實時下傳。另外后處理通常使用批處理最小二乘方式確定軌道，該算法精度較高，但僅適用于后處理或近實時處理。鑒于以上原因，后處理leo精密定軌無法滿足實時定軌需求。

綜上所述，現有的低軌衛星定軌方法無法提供實時的高精度leo軌道信息，無法滿足低軌衛星導航實時獲取高精度軌道的需求。

技術實現要素：

針對現有技術中存在的問題，為了提供實時的低軌導航衛星的精密軌道和時鐘信息，用以支持低軌導航衛星的精密定位應用，本發明公開了一種短弧段低軌導航衛星實時精密定軌方法。

一種短弧段低軌導航衛星實時精密定軌方法，該方法利用四臺或四臺以上地面接收機同時跟蹤若干顆gnss(全球導航衛星系統)導航衛星和leo(低軌)導航衛星的導航信號，并實時發送到數據中心，包括以下步驟：

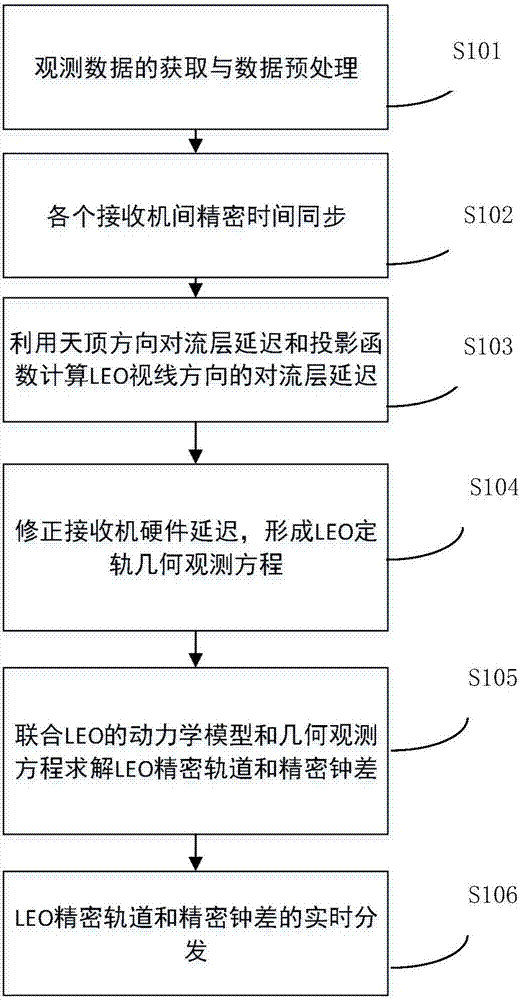
步驟一，觀測數據的獲取與數據預處理；

步驟二，各個接收機間精密時間同步；

步驟三，利用天頂方向對流層延遲和投影函數計算leo視線方向的對流層延遲；

步驟四，修正接收機硬件延遲，形成leo定軌幾何觀測方程；

步驟五，聯合leo的動力學模型和幾何觀測方程求解leo精密軌道和精密鐘差；

步驟六，leo精密軌道和精密鐘差的實時分發。

進一步地，所述導航信號包括gps，glonass，bds，galileo，irnss，qzss等衛星導航系統，導航信號內容包括偽距碼觀測值、載波相位觀測值和多普勒觀測值。

進一步地，所述時間同步采用絕對時間同步，其方法是數據中心利用各接收機接收到的導航衛星信號和從外部數據流解碼獲得的精密衛星軌道和鐘差信息，約束地面接收機坐標，采用濾波的方式解算精密的接收機鐘差、天頂方向對流層延遲和模糊度參數。

進一步地，所述絕對時間同步的解算方法如下：

導航衛星的偽距和載波相位觀測值表示為：

式(1)中：pi和φi分別表示第i個頻點的偽距和載波相位觀測值(以米為單位)，ρ表示衛星和接收機間的幾何距離，δt^s和δt^r分別表示衛星和接收機的時鐘偏差(以秒為單位)，ii和δtrop分別表示電離層和對流層延遲影響，ni表示第i個頻點的整周模糊度，εpi和εφi分別表示偽距和載波相位的接收機觀測噪聲，c表示真空中光速；λi表示第i個頻點載波波長(以米為單位)；

時間同步的觀測模型表示為：

式(2)中：e(·)為gnss觀測值向量，c為鐘差參數的系數矩陣，t為一個包含對流層投影函數的列向量作為天頂對流層延遲參數的系數矩陣，λ為模糊度參數的系數矩陣；

考慮到實時估計的需求和參數變化的非線性特征，參數估計使用擴展的卡爾曼濾波(ekf)實現；

考慮到接收機鐘差較好的短期穩定度和長期漂移特性，濾波過程中接收機鐘差參數使用隨機游走過程模擬，根據接收機鐘的質量和穩定度施加合適的過程噪聲；

采用隨機游走過程對對流層天頂方向濕分量影響進行模擬，對流層延遲量與導航信號傳播路徑有關，在參數化時利用對流層投影函數將各個接收機衛星視線方向的對流層延遲投影至測站天頂方向，記作

δtrop＝δtrop,z*mf(3)

式(3)中：δtrop表示信號視線方向對流層延遲，δtrop,z表示天頂方向對流層延遲，mf表示對流層投影函數，選擇一種投影函數實現對流層延遲從導航衛星信號視線方向到測站天頂方向的投影；

模糊度參數在接收機載波環正常鎖定的情況下當作常數，在載波環抖動或者失鎖的情況下，模糊度參數重置；

濾波完成后，獲得各個接收機鐘面時和gnss系統時之間的偏差以及各個接收機天頂方向的對流層延遲。

進一步地，所述對流層投影函數mf包括marini函數、chao函數、herring函數、neil投影函數(nmf)、global投影函數(gmf)、vienna投影函數(vmf)，還包括自定義投影函數和根據區域跟蹤網計算的投影函數。

進一步地，利用已知的各個接收機天線相位中心坐標和近似的leo衛星軌道計算leo衛星在各個接收機處的站心地平極坐標系坐標，即各個接收機觀測到的leo衛星信號的視線方向；利用測站坐標、信號發射時間以及leo衛星信號的視線方向，計算對流層投影函數，并利用該投影函數將上述估計得到的天頂方向對流層延遲投影到leo衛星信號的視線方向，獲得對流層延遲對leo導航信號的延遲量；使用實驗室標定、在線標定或等效時間基準的方式處理硬件延遲引起的時間系統偏差，將時間同步的參考時間基準從gnss系統時轉換到leo系統時。

進一步地，利用各接收機接收到的leo導航信號列出leo軌道確定的幾何觀測方程，leo導航信號觀測值表示為：

式(4)中：leo導航信號的衛星端鐘差作為參數估計，leo導航信號的接收機端鐘差通過參數估值和硬件延遲校正計算得到，電離層延遲誤差ii通過兩個leo導航頻點組成無電離層組合消除，幾何距離項ρ按照泰勒級數一階展開，可得:

式(5)中：ρ0為站星幾何距離近似值，dx、dy、dz表示近似leo軌道的改正數，x^s,y^s,z^s表示衛星三維坐標，x^r,y^r,z^r表示接收機天線相位中心三維坐標，ε是泰勒展開的高階項。

進一步地，聯合leo動力學模型和幾何觀測求解軌道鐘差的過程如下：

考慮到低軌衛星在空間運動，其受力情況表示為：

式(6)中：r，分別表示衛星位置、速度和加速度矢量，gm為地球重力場常數，fp為擾動加速度，q1,…,qd為d個待估動力學參數，動力學參數包括大氣阻力系數cd、太陽光壓系數cr和偽隨機脈沖參數等；

通過線性化的方法求解出加速度對各個參數的偏導數矩陣，得到狀態轉移矩陣φ(t,t0)，使用狀態轉移矩陣進行時間更新：

式(7)中：pt^-分別為t時刻時間更新后的狀態量及其方差協方差矩陣，分別為(t-1)時刻軌道狀態濾波解及其方差協方差矩陣，q(t)為過程噪聲矩陣。

進一步地，聯合動力學信息和幾何觀測信息進行軌道確定的卡爾曼濾波解可以表示為

上式中：kt為t時刻濾波增益矩陣，rt為幾何觀測值方差協方差矩陣。y為根據leo導航信號計算得到的幾何觀測信息向量。

進一步地，計算出濾波解后，還要對幾何觀測值的驗后殘差進行檢驗。濾波方程的驗后殘差估值可表示為：

根據驗后殘差估值可構造χ²檢驗量，服從χ²(n-t)分布，其中(n-t)表示自由度；若則認為驗后殘差通過檢驗，否則認為驗后殘差檢驗拒絕，式中是顯著性水平為α的閾值；如果驗后殘差檢驗未通過，則使用軌道預報解作為精密定軌輸出；如果驗后殘差檢驗通過，則使用濾波解作為精密定軌輸出。

進一步地，將上述計算得到的精密軌道和精密鐘差編碼成實時數據流格式，如rtcm，通過互聯網或者無線電臺的方式播發給用戶，用戶就可以使用收到的精密軌道和鐘差來計算；考慮到定軌計算和信息傳播的延遲，需要對收到的精密軌道和鐘差外推到用戶信號接收時刻，再參與地面定位解算。

與現有的方法相比，本方法具有以下優點：

1.能夠實時獲取低軌衛星短弧段的精密軌道和鐘差，產品的延遲時間主要是網絡數據傳輸造成的，僅為數秒，而該數據延遲造成的誤差影響可以通過數據外推有效的補償。

2.地面跟蹤設備價格低廉，僅需數臺定制化的gnss接收機，無需精密衛星跟蹤設備即可獲得高精度的衛星軌道。

3.監測網布設成本低，無需使用光纖、專用電纜等方法實現多接收機精密時間同步。

4.使用遞推濾波算法，濾波狀態參數維度低，計算效率高。

5.該定軌方法不受觀測條件、氣象等因素影響，有較強的環境適應能力。

6.該定軌方法同時適用于一顆leo定軌和多顆leo同時定軌的情況。

7.該定軌方法不要求leo衛星播發的導航信號與gnss導航信號精確同步，也不要求多顆leo衛星間導航信號時間系統精確同步。

附圖說明

圖1為本發明提出的短弧段低軌導航衛星實時精密定軌方法的原理示意圖。

圖2為本發明提出的短弧段低軌導航衛星實時精密定軌方法的流程圖。

圖3為本發明實施例提供的短弧段低軌導航衛星實時精密定軌方法中濾波算法流程圖。

具體實施方式

下面將結合附圖以及具體實施例來詳細說明本發明，其中的具體實施例以及說明僅用來解釋本發明，但并不作為對本發明的限定。

本發明提出的短弧段低軌導航衛星實時精密定軌方法原理如圖1所示。圖1中的meo，geo，igso分別指中軌道、地球同步軌道和傾斜同步軌道的導航衛星，包括但不限于gps，glonass，bds，galileo，irnss，qzss等全球或區域導航衛星系統的衛星；leo指具有導航測距信號發射功能的低軌道衛星。為了保證低軌道衛星能夠播發穩定的、高精度的測距信號，低軌衛星應配備馴服后的高穩晶振或原子鐘。圖1中的接收機是指能夠同時接收導航衛星和leo衛星導航信號、并能夠實時輸出高精度偽距和載波相位的測量型接收機。接收機應保證將leo衛星導航信號與gnss導航信號同步采樣。接收機應具有網絡通信功能或連接至具有網絡通信功能的數據轉發設備。圖1中的數據中心指至少1臺具有網絡通信功能的高性能服務器，并安裝了使用本發明論述的短弧段低軌導航衛星實時精密定軌方法實現的軟件。為了保證低軌衛星的軌道和鐘差可估，要求地面必須配備4臺或4臺以上的接收機同步觀測導航衛星和低軌衛星的導航信號，形成地面監測網絡。考慮到低軌衛星導航信號的地面覆蓋范圍直徑只有數千公里，地面接收機之間的間距建議選在1000km左右來獲得leo軌道較好的幾何觀測條件和較長的leo公共可見弧段。各個接收機對應天線的相位中心坐標需要事先精確測定，并且坐標應保證和gnss精密軌道在同一參考框架下。考慮到低軌衛星發射的導航信號頻點與導航衛星不同，接收機內部對不同頻率信號的硬件延遲也不同。對于單個可見的leo來說，接收機射頻元器件的硬件延遲偏差需要預先標定。各接收機應保證在leo衛星過境前、中、后連續穩定的工作，并且實時地將導航衛星、leo衛星的雙頻偽距和載波相位觀測值實時地、連續地發送至數據中心。圖1所示的各衛星(包括geo/igso/meo/leo)發射導航或測距信號，地面接收機負責導航信號的接收，數據中心負責軌道計算和分發。本發明涉及的計算方法均在數據中心執行。

本發明提出的短弧段低軌導航衛星實時精密定軌方法的詳細流程如圖2所示，下面對該流程圖進行詳細論述。

步驟101：觀測數據獲取與數據預處理；數據中心對收到的各個接收機的發過來的觀測數據進行解碼、校驗，確認無誤后逐個接收機進行數據預處理。數據預處理方法包括使用無幾何距離組合等方式進行數據掃描、檢測和標記異常數據及可能存在的載波相位周跳。

步驟102：接收機間精密時間同步；受到接收機鐘的頻率準確度和穩定度的限制，各個接收機的時鐘不是精確同步的，因此需要首先計算各個接收機鐘的鐘面時差異來進行時間同步。同步的方式有兩種，相對時間同步和絕對時間同步。相對時間同步是將所有接收機的鐘面時同步到某一個鐘的鐘面時。絕對時間同步是將所有接收機的鐘面時同步到外部的系統時間，如gps時或bds時。由于使用相對時間同步會導致最終確定leo鐘差與外部系統時之間存在偏差，建議使用絕對時間同步。絕對時間同步方法是指數據中心利用已知的各個接收機天線相位中心坐標，從外部數據流解碼獲得導航衛星精密的衛星軌道和衛星鐘差信息，采用濾波的方式解算精密的接收機鐘差，天頂方向對流層延遲和模糊度參數。解算方法如下：

導航衛星的偽距和載波相位觀測值可以表示為：

pi＝ρ+δorb+c(δt^s-δt^r)+ii+δtrop+εpi

φi＝ρ+δorb+c(δt^s-δt^r)-ii+δtrop+λini+εφi

上式中：pi和φi分別表示第i個頻點的偽距和載波相位觀測值(以米為單位)；表示衛星和接收機間的幾何距離，其中x^s,y^s,z^s表示衛星三維坐標，x^r,y^r,z^r表示接收機天線相位中心三維坐標；δt^s和δt^r分別表示衛星和接收機的時鐘偏差(以秒為單位)；ii和δtrop分別表示電離層和對流層延遲的影響；ni表示第i個頻點的整周模糊度；εpi和εφi分別表示偽距和載波相位的接收機觀測噪聲；c表示真空中光速；λi表示第i個頻點的載波波長(以米為單位)。

在步驟102中，接收機的天線相位中心坐標x^r,y^r,z^r可以事先精確測定，衛星坐標x^s,y^s,z^s可以通過精密星歷，衛星天線偏差文件精確計算，目前超快速gps衛星軌道誤差優于5cm。在數據處理中，幾何距離項ρ可以視為已知值，也可以考慮接收機天線相位中心坐標的不確定性，將接收機坐標作為未知參數進行估計，但同時根據其先驗的精度施加一個較強的約束。對于精密星歷，軌道誤差δorb可忽略。δt^s可通過實時估計的精密鐘差數據流改正。電離層延遲ii可通過無電離層組合消除，剩下的誤差項，包括接收機鐘差δt^r，對流層延遲δtrop和模糊度參數ni通過參數估計的方法處理。時間同步的觀測模型可表示為：

上式中：e(·)為gnss觀測值向量，c為鐘差參數的系數矩陣，矩陣列數與參與計算的衛星系統數相等。t為一個包含對流層投影函數的列向量作為天頂對流層延遲參數的系數矩陣。λ為模糊度參數的系數矩陣，對于載波相位觀測值，該矩陣為對角陣，每個對角線元素為對應載波相位觀測值的波長；對于偽距觀測值，該矩陣為零矩陣。如果載波相位觀測值不參與計算，則不考慮載波相位參數及其系數矩陣。

考慮到實時估計的需求和參數變化的非線性特征，參數估計使用擴展的卡爾曼濾波(ekf)實現。考慮到接收機鐘差較好的短期穩定度和長期漂移特性，濾波過程中接收機鐘差參數使用隨機游走過程模擬，根據接收機鐘的質量和穩定度施加合適的過程噪聲。常見的gnss接收機鐘包括(但不限于)溫補石英晶振(tcxo)、恒溫石英晶振(ocxo)、原子鐘，對于ocxo和原子鐘長期漂移緩慢，在一定時間內也可以當作隨機常數估計。由于接收機硬件延遲與信號頻率有關，對不同頻率的信號接收機端硬件延遲并不相同。如果接收機能夠同時跟蹤多個gnss系統的信號，應考慮不同gnss系統信號間的硬件延遲不同。因此，每個gnss系統應單獨估計一個接收機鐘差參數。以gps/bds雙模接收機為例，濾波模型中接收機鐘差向量應表示為由于gps和bds信號均采用同一個晶振，在接收機工作環境不變的情況下，和的變化趨勢一致。因此，接收機鐘差的另一種估計算法將接收機鐘差向量表示為該模型中仍采用隨機游走模型估計，可采用隨機常數模型估計，該項也被稱為系統間偏差(isb)。

根據中性大氣理論，對流層對電磁波延遲影響可以分為干分量和濕分量。干分量約占延遲的90％，并且可以用經驗模型很好的計算，濕分量和氣壓，大氣水汽分布有關，難以模型化，通常需要通過參數化的方式進行估計。對流層延遲量與導航信號傳播路徑有關，在參數化時可以利用對流層投影函數將各個接收機衛星視線方向的對流層延遲投影至測站天頂方向，記作

δtrop＝δtrop,z*mf

上式中：δtrop表示信號視線方向對流層延遲，δtrop,z表示天頂方向對流層延遲，mf表示對流層投影函數，常見的投影函數包括但不限于marini函數、chao函數、herring函數、neil投影函數(nmf)、global投影函數(gmf)、vienna投影函數(vmf)。選擇一種投影函數實現對流層延遲從導航衛星信號視線方向到測站天頂方向的投影。

在步驟102中采用隨機游走過程對對流層天頂方向濕分量影響進行模擬。模糊度參數在接收機載波環正常鎖定的情況下可以當作常數，在濾波器中也作為隨機常數估計。在載波環抖動或者失鎖的情況下，模糊度參數需要重置。濾波完成后，可獲得各個接收機鐘面時和gnss系統時(如gps時，bds時)之間的偏差，以及各個接收機天頂方向的對流層延遲。

步驟103：計算leo視線方向對流層延遲；利用精確已知的各個接收機天線相位中心坐標和近似的leo衛星軌道計算leo衛星在各個接收機處的站心地平極坐標系坐標，即各個接收機觀測到的leo衛星信號的視線方向。利用測站坐標，信號發射時間以及leo衛星信號的視線方向，計算對流層投影函數，并利用該投影函數將步驟102估計得到的天頂方向對流層延遲投影到leo衛星信號的視線方向，獲得對流層延遲對leo導航信號的延遲量。

步驟104：形成leo定軌幾何觀測方程；步驟102中時間同步是將各接收機的鐘面時同步到參考gnss系統(如gps系統)的系統時，對于leo軌道計算需要使用leo系統時作為參考。對于接收機而言，leo系統時和參考gnss系統的系統時之間差異由系統時間差和接收機硬件延遲兩部分組成。系統時間差可根據兩時間系統的系統定義計算，硬件延遲偏差是由于不同導航信號之間頻率不同導致的，該偏差與信號頻率，接收機射頻元器件，接收機硬件設計，固件，接收機工作環境有關。接收機硬件延遲是可以使用三種方法處理：實驗室標定，在線標定和等效時間基準。實驗室標定指在實驗室內測定接收機射頻元器件和硬件鏈路對不同頻率輸入的響應時延。在線標定是使用其他方式獲得的精密leo軌道和鐘差反算接收機硬件延遲。等效時間基準是對整個監測網使用同種型號接收機時，認為各接收機引起的硬件延遲相同。根據基準變換(s變換)原理，各接收機相同的硬件延遲被自動吸收到估計的leo衛星鐘差中，不會對leo軌道確定精度產生影響。標定參考gnss系統與leo系統的時間差后，再根據步驟102估計的gnss信號的接收機鐘差來推算相對于leo導航信號的接收機鐘差，以單gps接收機為例，推算公式為：

上式中：可從步驟102的估值中獲取，為預先在實驗室標定的兩頻點不同引起的硬件延遲偏差。為leo軌道確定需要使用的接收機鐘差。

若接收機為多模gnss接收機，如gps/bds接收機，則需要選擇某一衛星導航系統(如gps系統)為主衛星導航系統，并在實驗室內測定所有接收機leo導航信號與該主衛星導航系統頻率之間的硬件延遲偏差。再根據步驟102估計得到的該主衛星導航系統的接收機鐘差來確定接收機相對于leo導航信號的接收機鐘差。

利用各接收機接收到的leo導航信號列出leo軌道確定的幾何觀測方程，leo導航信號觀測值可表示為：

由于軌道參數是待估參數，因此不再將軌道誤差列入觀測誤差源。式中的幾何距離項ρ按照泰勒級數一階展開，可得:

上式中：ρ0為站星幾何距離近似值，可利用預先測定的測站坐標和通過廣播星歷計算的近似leo軌道計算。dx，dy，dz表示近似leo軌道的改正數，列入軌道估計濾波器的狀態向量。ε是泰勒展開的高階項，計算中通常忽略不計。leo導航信號的衛星端鐘差也作為參數估計。leo導航信號的接收機端鐘差可通過步驟102中的參數估值和硬件延遲校正計算得到。電離層延遲誤差ii可通過兩個leo導航頻點組成無電離層組合消除，或者使用電離層約束模型進行估計。考慮到大部分leo的軌道高度低于電離層總厚度，因此leo衛星播發的導航信號受到電離層影響小于meo，geo和igso導航衛星。在狀態向量中每一個估計一個電離層參數，并且在隨機模型中給該電離層參數設置一個合理的先驗方差信息，這樣可以有效的加快濾波收斂速度。考慮到所有地面接收機的觀測值，上式可表示為線性系統

y＝ax

其中位置參數向量x＝[dx,dy,dz,dt]，y為幾何觀測值，a為幾何觀測值線性化后的設計矩陣。

類似的，也可以利用多普勒觀測值將衛星的速度矢量和接收機鐘變化率表達成同樣的形式。

步驟105：聯合leo動力學模型和幾何觀測求解軌道鐘差；考慮到低軌衛星在空間運動受力情況可表示為：

上式中：r，分別表示衛星位置、速度和加速度矢量，gm為地球重力場常數，fp為擾動加速度，q1,…,qd為d個待估動力學參數。動力學待估參數通常包括大氣阻力系數cd，太陽光壓系數cr和偽隨機脈沖參數。r為衛星質心到地球質心間幾何距離。通過線性化的方法求解出加速度對各個參數的偏導數矩陣，稱為狀態轉移矩陣φ(t,t0)。考慮到計算復雜度，狀態轉移矩陣計算通常做一定的近似，常用的狀態轉移矩陣計算方法有goodyear法，markley法。求解出狀態轉移矩陣后，即可使用狀態轉移矩陣進行時間更新：

上式中：pt^-分別為t時刻時間更新后的狀態量及其方差協方差矩陣，分別為(t-1)時刻軌道狀態濾波解及其方差協方差矩陣。q(t)為過程噪聲矩陣。考慮到線性化后的幾何觀測方程，軌道確定的卡爾曼濾波解可以表示為

kt＝pt^-a(apt^-a^t+rt)^-1

pt⁺＝(i-kta)pt^-

上式中：kt為t時刻濾波增益矩陣，rt為幾何觀測值方差協方差矩陣。計算出濾波解后，還需要對幾何觀測值的驗后殘差進行檢驗，如果檢驗未通過，則僅使用時間更新的解作為最終定軌結果；如果檢驗通過，則使用濾波解作為最終定軌結果。然后開始下一歷元軌道計算。

步驟106：leo精密軌道和鐘差的實時分發；將步驟105計算得到的精密軌道和精密鐘差編碼成實時數據流格式，如rtcm，通過互聯網或者無線電臺的方式播發給用戶，用戶就可以使用收到的精密軌道和鐘差來計算。考慮到定軌計算和信息傳播的延遲，通常需要對收到的精密軌道和鐘差外推到用戶信號接收時刻，再參與地面定位解算。

本發明與現有后處理精密定軌的顯著區別之一就是本發明使用卡爾曼濾波算法確定實時軌道，而不是批處理最小二乘算法。濾波流程已在步驟105中有所涉及，下面對濾波算法進行更詳細的介紹。本發明實施例提供的短弧段低軌導航衛星實時精密定軌方法中濾波算法流程如圖3所示。

步驟201:初始化軌道狀態向量。初始化軌道狀態向量指濾波開始時刻的近似的leo衛星位置矢量r和速度矢量衛星初始的軌道參數可以使用leo廣播的軌道。如果leo播發的信號不包括廣播星歷，也可以使用步驟101～步驟104計算得到的信息使用逆向的單點定位計算求解初始衛星軌道。衛星初始軌道通常只需要數米級的精度，因此普通的星上自主定軌即可滿足要求。由于本發明使用的是kalman濾波計算，軌道計算會有一個收斂過程，而收斂過程時間長短與近似坐標準確程度有關。

步驟202：軌道積分；根據leo衛星的初始軌道狀態，分析衛星的受力情況，再利用衛星的受力與運動的關系通過積分的方式預報衛星速度和位置。自由飛行的leo在軌衛星受到力主要包括重力、多體引力、太陽輻射壓、大氣阻力、地球輻射壓、地球潮汐、未模型化的力。其中重力可分解為正常重力和重力攝動項。正常重力可以使用已知的地球常量直接計算，地球的攝動項可以展開表示成一定階次的球諧函數來逼近。目前已有多種重力場模型給出了各自的球諧函數系數，如jgm3，egm96，egm2008等。應用這些重力場模型，選擇合適的階次，即可計算出相應精度的重力場模型。米級精密定軌通常選用30～50階次的重力場模型，厘米級精密定軌則選用90～120階次的重力場模型。模型階次越高，計算量越大，計算耗時越長。多體引力主要是使用星表，如jplde200，jplde405星表，計算其他星體慣性系坐標，再根據相應星體的天文常數確定該星體對衛星的吸引力。米級定軌通常只考慮日月引力，精密定軌還考慮太陽系其他行星的吸引力。太陽輻射壓和衛星表面材質，衛星與太陽光線的夾角等有關。米級定軌使用經驗的反射系數，精密定軌需要估計衛星三個面的反射系數cr。衛星進入地影區不受太陽輻射壓影響。大氣阻力主要和衛星軌道處的大氣密度，衛星表面阻尼系數，衛星面質比和衛星速度有關。其中大氣密度通常使用經驗模型，如harris-priester模型、jacchia-lineberry模型計算，衛星三個方向的面質比可根據衛星參數確定，表面阻尼系數cd在米級定軌中使用經驗參數，在精密定軌中作為參數估計。地球輻射壓、地球潮汐可根據模型計算，未模型化的力在米級定軌中忽略，在精密定軌中使用經驗力或者偽隨機脈沖吸收。

leo衛星某一時刻受到的力等于以上各個力的合力。根據牛頓運動定律，可根據衛星的受力計算衛星的加速度，進而積分得到衛星的速度。由于衛星的受力非常復雜，難以使用解析的方法進行積分計算，通常都使用數值積分的方法逼近，常見的單步數值積分方法有4階runge-kutta-fehlberg方法(rkf4)，4階runge-kutta方法(rk4)等，也有使用多步積分、變階次、變步長等更復雜的數值積分方法，如stoermer-cowell積分法。通過數值積分的方法，就可以根據初始軌道x0預報其他時刻的衛星軌道

步驟203：求解狀態轉移矩陣；狀態轉移矩陣是當前的衛星狀態和衛星加速度對所有參數計算一階導數。重力場加速度(含攝動項)對衛星軌道向量[x，y，z]的偏導數可用cunningham方法計算。多體引力、太陽輻射壓、大氣阻力等對濾波狀態向量的偏導數均可使用公式直接計算。類似地，狀態轉移矩陣也需要先計算某一時刻的狀態轉移矩陣后，再使用數值積分的方法進行遞推到指定時刻。由于狀態轉移矩陣計算牽涉導數計算，通常在計算中做一定程度的近似，因此狀態轉移矩陣遞推沒有步驟202中論述的數值積分精度高，通常用來方差協方差矩陣的時間更新計算。

步驟204：處理幾何觀測值；幾何觀測值處理主要包括利用已知的地面站坐標和近似leo軌道計算近似站星幾何距離，改正地面接收機鐘差，對流層延遲，消除電離層延遲等方面，詳細的計算方法在步驟102和步驟103中闡述。

步驟205：列幾何觀測方程；leo衛星的幾何觀測量可使用泰勒級數展開，取一階項，近似轉化為線性系統，具體的列幾何觀測方程的方法在步驟104中闡述。

步驟206：濾波求解軌道；聯合幾何觀測和動力學模型，使用擴展的kalman濾波(ekf)方法求解leo的精密軌道、速度和鐘差。具體的濾波方法在步驟105中闡述。

步驟207：驗后殘差檢驗；濾波方程的驗后殘差估值可表示為：

根據驗后殘差估值可構造χ²檢驗量，服從χ²(n-t)分布，其中(n-t)表示自由度。若則認為驗后殘差通過檢驗，否則認為驗后殘差檢驗拒絕。式中是顯著性水平為α的閾值。如果驗后殘差檢驗未通過，則使用軌道預報解作為精密定軌輸出；如果驗后殘差檢驗通過，則使用濾波解作為精密定軌輸出。

以上所述僅為本發明的較佳實施例，并不用以限制本發明，凡在本發明的精神和原則范圍之內所作的任何修改、等同替換和改進等，均應包含在本發明的保護范圍之內。