在軌X射線脈沖星計時模型構建方法與流程
本發明涉及天文導航領域,尤其涉及一種在軌x射線脈沖星計時模型構建方法。
背景技術:
x射線脈沖星導航是一種新型自主導航方式,可以在單一儀器上自主完成航天器位置、速度和時間等信息測量,能夠為近地、深空以及行星際飛行航天器提供有效的導航與授時解決方案,被認為是未來深空自主導航領域最具潛力的導航與授時方式之一。
構建x射線計時模型是脈沖星導航系統的基礎性工作。對于脈沖星自主導航而言,隨著傳輸距離的增加以及星際遮擋等原因,無法依靠地面測控系統實時、連續地傳輸射電計時模型參數,此外,當導航脈沖星存在周期躍變等自轉周期不規則現象時,需要利用x射線觀測數據,重新評估原模型參數,并建立新的脈沖星計時模型。因此,利用x射線觀測數據獨立自主地建立計時模型對航天器自主導航具有明顯的支撐作用。
構建x射線計時模型是獲得脈沖星時的關鍵技術。脈沖星輻射的信號的重復周期均勻性好、頻率間隔精度高、并且能連續穩定運行,符合公認的鐘的原理與特征,在建立脈沖星時過程中,需要描述脈沖星的自轉頻率、脈沖到達時間與原子時的數學關系,因此,精確的脈沖星計時模型是分析和建立脈沖星時的關鍵環節。
構建x射線計時模型還是脈沖星輻射機理研究的重要補充手段。對于有些類型的脈沖星,比如psrj0205+6449,先測到x射線接著才測到射電波段信號,隨著x射線巡天的深入開展,未來會發現更多此類脈沖星,在未知其射電計時模型時,建立其x射線計時模型研究其輻射機理就顯得至關重要。同時,建立x射線計時模型還可以與射電計時模型相互驗證,為射電計時模型中存在的色散等誤差源提供參考。
2016年10月8日,我國的“脈沖星試驗衛星”成功發射,目前也已將構建x射線計時模型列為此次觀測試驗的一項科學和技術目標。
由于脈沖星在射電和x射線電磁波段均有輻射,所以脈沖星計時模型又可以分為射電計時模型和x射線計時模型,但與射電計時數據處理相比,x射線觀測主要存在以下兩個主要問題:
(1)x射線觀測平臺的動態性高。射電觀測平臺是地面的射電望遠鏡,而x射線觀測平臺則是星載x射線探測器。由于脈沖星觀測可以認為是一種相對觀測,地球自轉周期24小時,而近地軌道衛星的自轉周期僅100分鐘,射電觀測站的角加速度要遠遠低于衛星平臺,兩種平臺的動態性會給信號處理帶來較大差異,從而影響時間校正方法。
(2)x射線信號強度弱,射電信號通過大型天線也能轉換成電信號,而x射線是隨機分立的光子信息,這種弱信號的特性給x射線數據處理方法帶來了很大的不同,包括到達時間校正方法、頻率搜索方法、脈沖toa估計方法、以及在初始相位不精確條件下,計時模型的代價函數設計等,這些方法均需要重新改正與設計。
現有的射電計時模型處理方法較為成熟,但由于x射線數據形式、平臺動態、信號強度等與射電觀測有很大的差異,尤其是以上兩個問題的存在,需要改進和設計x射線計時模型構建方法。
技術實現要素:
本發明的目的在于提供一種利用x射線觀測數據計算脈沖星計時模型的方法框架。
本發明提供一種在軌x射線脈沖星計時模型構建方法,步驟一,x射線脈沖星光子到達時間預處理:將近地軌道航天器探測的光子到達時間的固有時轉換到太陽系質心坐標系下的坐標時,對于航天器處測量的x射線光子到達時間假設用τobs表示,那么相應的ssb處的光子到達時間為
tssb=τobs+△i+△c+△p+△r+△e+△s
公式中,△i為儀器響應延遲,用于修正x射線探測器的硬件響應時間延遲;
△c是時鐘校正,該項校正由于記錄x射線到達時間的原子鐘長期穩定度降低而引入的時間誤差;
△p是周年視差校正,校正地球繞太陽周年運動所產生的視差;
△r是roemer延遲,在真空中傳播的同一光脈沖從航天器位置到ssb處的時間差;
△e為太陽系einstein延遲,該項是校正由于地球的運動,以及地球的引力勢在衛星位置和ssb處的不同而導致的時延;
△sshapiro延遲,該項是校正光在經過太陽系內大質量天體時所引入的時間延遲;
步驟二,高精度的脈沖星自轉頻率計算:假設第i個光子到達時間分別用ti表示,對于假定的自轉頻率f,那么每個光子相位可以表示為
φi=2πmod(fti,1)
mod為取余運算符,那么一種高精度的
其中的
最優的參數m的快速計算方法為
式中:
步驟三,計時模型的初值區間估計:在建模x射線脈沖星計時模型時,需要計算并估計頻率參數的初值區間;
步驟四,觀測脈沖輪廓重構:在獲得步驟二中的各數據包的自轉頻率后,利用歷元折疊的方法獲取觀測脈沖輪廓;
步驟五,高精度的脈沖到達時間估計:根據觀測脈沖輪廓模型估計初始相位的似然函數,計算脈沖峰值的達到時間。
與相關技術相比,本發明提供的在軌x射線脈沖星計時模型構建方法避免了傳統的卡方量估計方法精度低帶來的問題,同時解決了解決傳統小波變換對脈沖輪廓消噪處理導致的信號急劇變化部分產生的震蕩現象,同時保留脈沖輪廓的線性相位,提高計算精度。
附圖說明
圖1為本發明提供的在軌x射線脈沖星計時模型構建方法流程圖;
圖2本發明利用
圖3為對7組衛星數據搜索的頻率擬合的結果示意圖;
圖4為初始相位誤差為0.2時,傳統頻率搜索代價函數得到的結果示意圖;
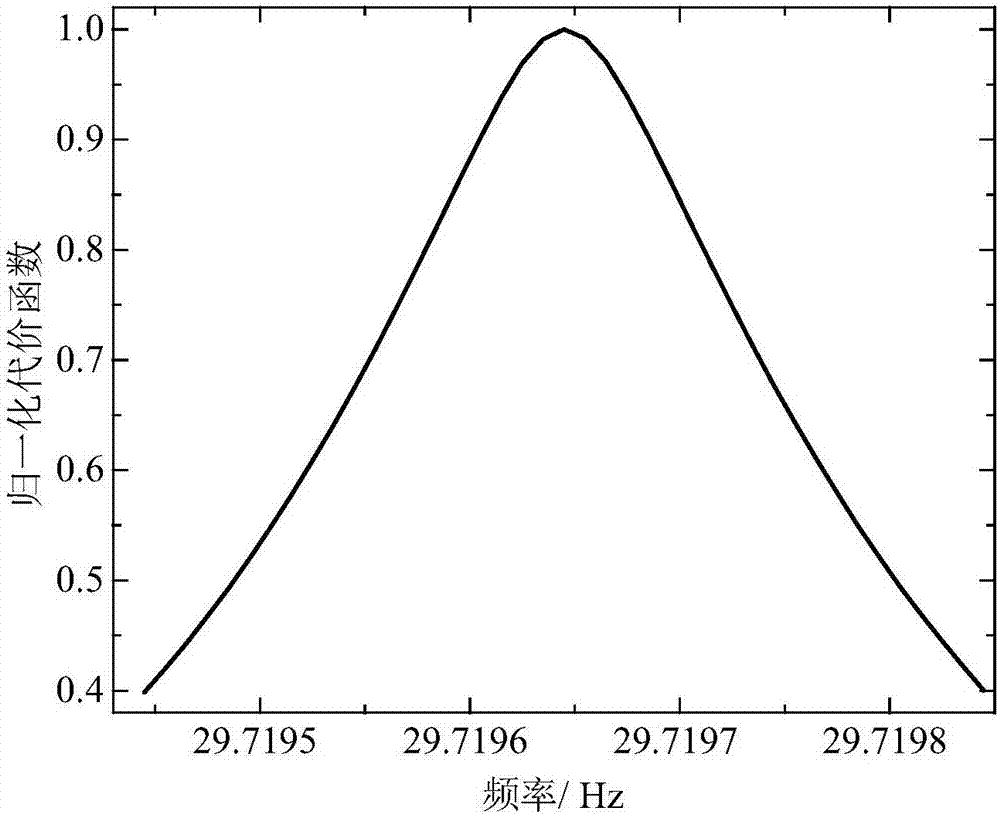
圖5為初始相位誤差為0.2時,本發明提出的頻率搜索代價函數得到的結果示意圖。
具體實施方式
以下將參考附圖并結合實施例來詳細說明本發明。
如圖1所示,所述在軌x射線脈沖星計時模型構建方法包括如下步驟:
1、x射線脈沖星光子到達時間預處理:將近地軌道航天器探測的光子到達時間的固有時轉換到太陽系質心坐標系下的坐標時,對于航天器處測量的x射線光子到達時間假設用τobs表示,那么相應的ssb處的光子到達時間為
tssb=τobs+△i+△c+△p+△r+△e+△s
公式中,△i為儀器響應延遲,用于修正x射線探測器的硬件響應時間延遲;
△c是時鐘校正,該項校正由于記錄x射線到達時間的原子鐘長期穩定度降低而引入的時間誤差;
△p是周年視差校正,校正地球繞太陽周年運動所產生的視差;
△r是roemer延遲,在真空中傳播的同一光脈沖從航天器位置到ssb處的時間差;
△e為太陽系einstein延遲,該項是校正由于地球的運動,以及地球的引力勢在衛星位置和ssb處的不同而導致的時延;
△sshapiro延遲,該項是校正光在經過太陽系內大質量天體時所引入的時間延遲。
該步驟與射電計時觀測數據處理的差別:1)射電需要進行大氣色散校正、星際色散校正,而x射線計時觀測數據處理并不需要;2)射電僅需要對某個脈沖到達時間的固有時校正,而x射線需要對所有光子到達時間的固有時進行校正。
2、高精度的脈沖星自轉頻率計算:假設第i個光子到達時間分別用ti表示,對于假定的自轉頻率f,那么每個光子相位可以表示為
φi=2πmod(fti,1)
mod為取余運算符,那么一種高精度的
其中的
最優的參數m的快速計算方法為
式中:
利用
該步驟與現有頻率計算方法的差別在于,這里提出一種
3、計時模型的初值區間估計:在進行x射線脈沖星計時模型建模時,需要利用頻率參數的初值區間。這里給出了一種基于最小二乘法的頻率參數初值估計方法。
(1)將步驟二估計的m個數據包的脈沖星自轉頻率參數記為{(△t1,f1),(△t2,f2),…,(△tm,fm)},其中△ti=ti-t0,即觀測時間與參考時間t0的時間間隔,那么測量數據可以表示為y=[f1,f2,…,fm]t,要估計的參數向量表示為β=[f(l)/l!,f(l-1)/(l-1)!,…,f(0)/0!]t,根據最小二乘法,有以下關系成立
y=xβ+ε
其中的x用矩陣的形式展開為
(2)待估計的參數向量可以表示為
其中的r、q分別是矩陣x進行qr分解的上、下三角矩陣;
(3)
(4)對于
其中,βi=f(i)/i!,tα/2(m-l-1)為學生氏t分布,置信水平為α,cii為矩陣(xtx)-1第i行、第i列的元素,方差的無偏估計量
如圖3所示,利用最小二乘法確定的頻率范圍(29.48,29.96),頻率一階導數范圍(-5.543×10-10,1.279×10-9),頻率二階導數范圍(-1.564×10-18,1.731×10-19)。經過該步驟,就可以為計時模型中的各頻率參數提供初始估計區間。
4、觀測脈沖輪廓重構:在獲得步驟二中的各數據包的自轉頻率后,利用歷元折疊的方法獲取觀測脈沖輪廓。
(1)選擇各數據包的中點時刻tmid作為歷元折疊的參考時間。
(2)計算光子到達時間相對于中點參考時間的相位,對于第i個數據包,其相應的光子到達相位為φj=fi(tj-tmid)。
(3)借助歷元折疊方法計算觀測脈沖輪廓
式中:n0為初始相位φ(t0)引入的相位整數,nb是歷元折疊的bin塊數量,np為積分時間內包含的整周期,tobs≈np/f,ci,k是第i個整相位第k個bin塊內的光子數。
(4)借助具有平移不變性質的小波變換對觀測脈沖輪廓進行消噪處理,此處使用平移不變小波消噪,以解決傳統小波變換對脈沖輪廓消噪處理導致的信號急劇變化部分產生的震蕩現象,同時保留脈沖輪廓的線性相位,以便于后續的脈沖到達時間估計處理。
5、高精度的脈沖到達時間估計:利用每個bin內的光子計數值
式中:λ(φ)為標準速率函數,觀測脈沖輪廓
其相對于φ0的最大值即可得到φ0的最大似然估計值
其中:
脈沖到達時間差d可以表示為
脈沖峰值的到達時間為
tpk=tmid+d。
該步驟提出一種快速最大似然脈沖到達時間估計方法,計算脈沖峰值的到達時間,該步驟中使用快速最大似然方法,具更高的計算精度。
6、魯棒的計時模型估計:該方法對初始參考頻率參數敏感,當初始參考頻率參數區間的誤差較大時,由于光子到達時間相位取整過程發生變化,導致估計精度降低,甚至產生錯誤估計。這里提出了一種魯棒的頻率估計方法,頻率搜索的代價函數設計如下:
(1)根據步驟三的計算結果,設置
(2)設置
(3)計算在各假定頻率參數下的頻率搜索的代價函數χ2(β)。
(4)將多維問題轉換為一維的量,繪制代價函數χ2(β)曲線
(5)計算代價函數χ2(β)曲線的最小值,計算相應的頻率參數值
該方法克服了傳統方法在頻率區間誤差較大時,計算的計時模型出錯的問題,而且該方法還可以在初始相位位置的條件下進行計算,計算方法的魯棒性得到大大加強。
如圖4、圖5所示,當初始相位誤差為0.2時,利用傳統的計時模型構建方法得到的代價函數是發散的,代價函數的整體誤差較大,在中心頻率處也沒有有效地降低,利用傳統代價函數得到的參數估計結果為:頻率估計誤差為﹣3.5×10-4,頻率一階導數估計誤差為4.69×10-13,頻率二階導數估計誤差為1.97×10-20。而利用本發明的方法,代價函數在中心頻率處的代價函數值迅速減小,頻率估計誤差為﹣5.9067×10-9,頻率一階導數估計誤差為9×10-15,頻率二階導數估計誤差為9.7×10-21。
從參數估計結果的比較來看,本發明提出的方法能夠有效地降低初始相位誤差對估計精度的影響,具有較好的魯棒性。
以上所述僅為本發明的實施例,并非因此限制本發明的專利范圍,凡是利用本發明說明書及附圖內容所作的等效結構或等效流程變換,或直接或間接運用在其它相關的技術領域,均同理包括在本發明的專利保護范圍內。
- 還沒有人留言評論。精彩留言會獲得點贊!