基于導向矢量失配估計的魯棒波束域自適應波束形成方法與流程

本發明涉及陣列信號處理領域，尤其涉及一種基于導向矢量失配估計的魯棒波束域自適應波束形成(adbf)方法。

背景技術：

自適應波束形成(adbf)是將傳統相控陣雷達中射頻復加權移至數字基帶上的波束形成技術，其核心思想是約束天線主波束保形條件下，在干擾入射空間角對干擾的波束方向圖進行自適應置零，從而實現干擾抑制，因此具有更高的分辨率和更強的干擾抑制能力，并且這些特性都是建立在期望信號導向矢量等信息精確己知的前提下。然而數字陣列在工作時，會面臨諸如陣元間互耦、幅相誤差、陣元位置誤差等誤差因素的影響，其中誤差因素造成導向矢量失配使得目標輸出信干噪比性能急劇惡化。

波束域adbf算法將陣元數據轉換到波束域，提供了干擾角度和干擾源數目信息，設計針對干擾源的輔助波束，實現對波束域的降維處理，提高了收斂速度，然而當誤差因素造成目標導向矢量與波束指向失配時，波束域adbf算法不能自適應地修正目標導向矢量失配誤差，使得其輸出信干噪比急劇下降，嚴重影響其性能。因此本章對目標導向矢量與波束指向失配開展研究，這對提高自適應波束形成輸出信噪比具有十分重要的意義。

因此，本專利是針對目標導向矢量與波束指向失配進行研究分析，提出了基于導向矢量失配估計的魯棒波束域adbf形成方法，能夠有效解目標導向矢量與波束指向失配問題同時提高自適應波束形成輸出信噪比。

技術實現要素：

本發明所要解決的技術問題是針對背景技術中所涉及到的缺陷，提供一種基于導向矢量失配估計的魯棒波束域自適應波束形成方法。

本發明為解決上述技術問題采用以下技術方案：

一種基于導向矢量失配估計的魯棒波束域自適應波束形成方法，包括如下步驟：

步驟1)，令m陣元的均勻線陣的各陣元天線各項同性，有k個干擾源，其方位入射角分別為[θ1，θ2，...θk]，線陣接收信號為：x＝sa+n；

其中，為各干擾信號接收復包絡的集合，為各干擾信號的陣列流形的集合，m為陣元的個數，n為系統噪聲，第i個干擾信號陣列流形為：

其中，θi為第i個干擾入射角，d為陣元間距，λ為雷達波長，上標t表示轉置符號；

陣列協方差矩陣r表示為：其中g表示預設的訓練樣本的快拍數；

步驟2)，信號與干擾子空間計算：

當目標導向矢量與波束指向匹配時，信號與干擾子空間ur由協方差矩陣r的q個最大特征值對應的特征向量組成，q表示信號與干擾子空間的維數，其在子空間的投影矩陣表示為urur^h；

當目標真實的導向矢量a(t)與波束指向角對應的導向矢量存在失配時，信號加干擾子空間就變為ur(δ)：

ur(δ)＝[p{q(δ)}[u1...uq]]

其中，q(δ)是正定矩陣，表示觀察方向，δ表示陣列主瓣寬度對應的空域覆蓋角度，φ為陣列主瓣寬度對應的空域覆蓋角度的積分變量，p{q(δ)}為q(δ)的最大的特征值對應的特征向量，um表示協方差矩陣r的第m個按遞減順序排序的特征值對應的特征向量，1≤m≤q；

步驟3)，目標導引矢量與波束指向角失配誤差估計：

令為a(t)與之間的失配矢量，則其能夠被分解為兩非零的正交向量和分別位于信號子空間與干擾子空間；

其中，||·||2表示歐氏范數，上標h表示共軛轉置；

步驟4)，拉格朗日算子計算：

基于失配矢量的歐氏范數來設計波束域的權值：

其中，ε表示不確定等級，表示歐氏范數的平方；

為了避免公式收斂到零解，使

采用拉格朗日乘子法：

對l(a(t),μ)關于a(t)進行求導，并令得到：

整理得最優的目標信號導向矢量為：

最后得到關于拉格朗日算子μ的方程：i表示單位矩陣；

步驟5)，陣列主瓣寬度對應的空間覆蓋角度計算：

δ滿足：δ≥0；通過在陣列主瓣寬度對應的空域覆蓋角度范圍內對δ進行掃描，獲得使最小值的δ，更新ur(δ)，利用ur(δ)得到不確定等級ε，即：

步驟6)，目標最優的信號導向矢量的計算：根據步驟4)和5)，利用步驟5中得到的ε計算拉格朗日算子μ：

其中，τmax表示γ矩陣對角線上的最大特征值，u表示協方差矩陣r的所有特征向量組成的正交矩陣，由此得出目標最優的信號導向矢量

其中，γ表示協方差矩陣r的所有特征值組成的對角矩陣；

步驟7)，魯棒波束域adbf的權值的計算：

步驟7.1),對估計的導引矢量進行歸一化處理，即

步驟7.2)，經幅相加權后實現和波束方位超低副瓣，輸出信號

步驟7.3),采用music算法獲取干擾空間角，當存在k個干擾時，干擾輔助波束輸出為：

c＝fk^hx

其中，fk＝[sk_1sk_2…sk_k]，θk_i為第i個干擾入射角估計值，sk_i為第i個干擾信號的陣列流形；

步驟7.4),獲得魯棒波束域adbf的權值：

其中，rc＝e[c^hc]，rcz_new＝e[z^hnewc]，由預設的訓練樣本估計得到。

本發明采用以上技術方案與現有技術相比，具有以下技術效果：

解決了傳統波束域adbf算法忽略目標導向矢量與波束指向失配問題，有效提高了波束域adbf的輸出信噪比和收斂速度，與未考慮目標導向矢量與波束指向角失配的波束域adbf算法相比，采用本發明校正兩者間的失配誤差后，魯邦波束域adbf的輸出信噪比提高了約5db。

附圖說明

圖1為魯棒波束域adbf原理圖；

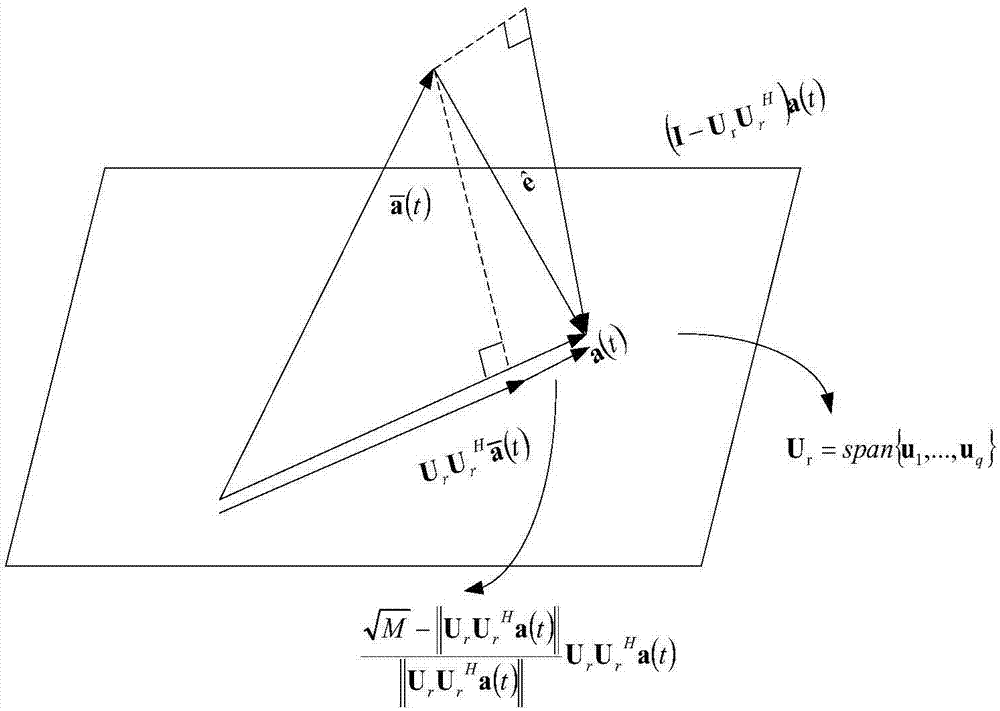
圖2為子空間關系的幾何解釋；

圖3為魯棒波束域adbf算法流程圖；

圖4為目標導向矢量誤差隨目標輸入信干比的變化圖；

圖5為目標輸出信噪比隨觀測角度變化圖；

圖6為歸一化自適應天線方向圖；

圖7為波束域adbf和魯棒波束域adbf目標輸出snr圖。

具體實施方式

下面結合附圖對本發明的技術方案做進一步的詳細說明：

令m陣元的均勻線陣的各陣元天線各項同性，有k個有源干擾，其方位入射角分別為[θ1θ2…θk]，線陣接收信號為：

x＝sa+n(1)

其中，為各干擾信號接收復包絡的集合，為各干擾信號的陣列流形的集合，m為陣元的個數，n為系統噪聲，干擾信號陣列流形為

其中，θi為干擾入射角，d為陣元間距，λ為雷達波長，上標^t表示轉置符號。

假定數字陣列波束指向為θ0，其主波束導引矢量為：

波束域adbf算法經幅相加權后實現和波束方位超低副瓣，輸出信號為：

z＝a(θ0)^hx(4)

采用music算法獲得干擾空間角，然后在波束域選取針對干擾方向的輔助波束，當存在k個干擾時，其輔助波束輸出為：

c＝fk^hx(5)

其中，fk＝[sk_1sk_2…sk_k]，θk_i為第i個干擾入射角估計值，sk_i為第i個干擾的導向矢量。最后利用干擾輔助波束對消常規和波束中的干擾信號，即：

其中，rc＝e[c^hc]，rcz＝e[z^hc]，由預設的訓練樣本估計得到。

存在干擾的條件下波束域adbf方法的自適應天線方向圖為：

σθ＝σθ-wrdgc(7)

其中：σθ、gc分別為常規和波束方向圖與輔助天線方向圖。

自適應波束形成問題本質上是設計最優權重向量來最大限度的減少干擾加噪聲的輸出功率，提高陣列輸出的信干噪比：

其中，a(t)表示目標信號的導向矢量，t表示目標指向角度，r表示信號加干擾協方差矩陣，w表示自適應波束形成最優權重矢量。協方差矩陣r表示為：其中g表示預設的訓練樣本的快拍數。

當目標導向矢量與波束指向匹配時，信號加干擾子空間ur由協方差矩陣r的q個最大特征值對應的特征向量組成，q表示信號與干擾子空間的維數，其在子空間的投影矩陣可表示為：urur^h。但當目標真實的導向矢量a(t)與假設的導向矢量不匹配時，如圖2所示，信號加干擾子空間就變為ur(δ)，可表示為：

ur(δ)＝[p{q(δ)}[u1...uq]](9)

其中，q(δ)是一個正定矩陣，p{q(δ)}為q(δ)的最大特征值對應的特征向量，可表示為：

其中，表示觀察方向，δ表示陣列主瓣寬度對應的空域覆蓋角度，φ為陣列主瓣寬度對應的空域覆蓋角度的積分變量，um表示協方差矩陣r的第m個特征值對應的特征向量，其中r特征值按遞減順序排序，1≤m≤q。在一定信噪比條件下，δ＝0，ur(δ)近似等于ur。因此可以通過所給的失配矢量的歐氏范數來設計波束域的權值：

其中ε表示不確定等級，表示歐氏范數的平方。

為了避免公式(11)收斂到零解，必須使：

采用拉格朗日乘子法：

對l(a(t),μ)關于a(t)進行求導，并令整理得到最優的目標信號導向矢量為：

將公式(13)帶入約束條件(12)中，得到關于拉格朗日算子μ的方程：

其中，i表示單位矩陣。

令為a(t)與之間的失配矢量，即：從圖1可以看出，被分解為兩非零的正交向量，分別位于信號子空間與干擾子空間，即和由此，失配矢量可被近似表示為：

其中，上標h表示共軛轉置，||||2表示歐氏范數。陣列主瓣寬度對應的空間覆蓋角度δ滿足：

通過在陣列主瓣寬度對應的空域覆蓋角度范圍內對δ進行掃描，獲得使最小值的δ，更新ur(δ)。結合波束域adbf算法，圖3給出了魯棒波束域adbf算法流程圖。

下面通過計算機仿真驗證本專利的有效性。雷達系統仿真參數如表1所示；假定無源探測系統數字陣列接收信號中存在三個有源干擾，其入射空間角分別為：-60°、-40°、60°，每個干擾陣元的干噪比為20db。以下仿真計算結果均為100獨立蒙特卡洛實驗的平均值。

表1雷達系統仿真參數

采用均方根誤差(rmse)來量化分析基于魯棒adbf算法的導向矢量的精度。y為總實驗次數，則均方根誤差定義為：

式中：表示第y次試驗目標方位角的估計值，θ'表示實際目標方位角。圖4給出了目標角度估計rmse隨目標輸入信干比的變化曲線，隨著目標輸入信干比的提高，魯棒波束域adbf的導向矢量誤差在逐漸降低最終趨近于0。

當目標輸入信干比為0db，干噪比為10db，圖5給出了不同波束指向角條件下的輸出信噪比曲線。實驗結果可知：魯棒波束域adbf的目標輸出信噪比隨著目標觀測角度的變化幾乎不變，穩定在28db左右，而波束域adbf的目標輸出信噪比則發生著不規律的變化。圖6給出了魯棒波束域adbf算法的自適應天線方向圖。可見，經過導引矢量失配估計，修正的波束指向與目標真實位置一致，位于7°處，這進一步驗證了本文算法的準確性。

圖7給出了不同目標輸入信干比條件下的目標輸出信噪比曲線。實驗結果可知：波束域adbf的輸出性能明顯低于魯棒波束域adbf；當目標輸入信干比在-10db時，由于導引矢量估計誤差，魯棒波束域adbf性能與波束域adbf性能相當，但隨著目標輸入信干比的增大，魯棒波束域adbf的目標輸出信噪比越來越接近目標最優輸出信噪比，在目標輸入信干比為0db時，魯棒波束域adbf的目標輸出信噪比比波束域adbf的目標輸出信噪比約大5db左右。

本發明針對目標導向矢量與波束指向失配的問題，提出了一種基于導向矢量失配估計的魯棒波束域自適應波束形成方法。文中提出了首先獲取目標導向矢量的失配矢量，然后構建信號加干擾子空間，進而通過所給的失配矢量的范數來估計目標導向矢量，最后獲得魯棒波束域adbf的權值。仿真結果表明，與未考慮目標導向矢量與波束指向角失配的波束域adbf算法相比，采用本發明校正兩者間的失配誤差后，魯邦波束域adbf的輸出信噪比提高了約5db。算法收斂速度快，易于工程實施。

本技術領域技術人員可以理解的是，除非另外定義，這里使用的所有術語(包括技術術語和科學術語)具有與本發明所屬領域中的普通技術人員的一般理解相同的意義。還應該理解的是，諸如通用字典中定義的那些術語應該被理解為具有與現有技術的上下文中的意義一致的意義，并且除非像這里一樣定義，不會用理想化或過于正式的含義來解釋。

以上所述的具體實施方式，對本發明的目的、技術方案和有益效果進行了進一步詳細說明，所應理解的是，以上所述僅為本發明的具體實施方式而已，并不用于限制本發明，凡在本發明的精神和原則之內，所做的任何修改、等同替換、改進等，均應包含在本發明的保護范圍之內。