一種基于時間代價函數的時間窗路徑規劃沖突解決方法與流程
本發明屬于路徑規劃領域,特別涉及一種基于時間代價函數的時間窗路徑規劃沖突解決方法。
背景技術:
agv最早出現于上世紀50年代,可配備電磁或光學導引裝置,同時配置可編程模塊供開發人員靈活使用,是一種無人駕駛的智能化搬運設備,是現代工業自動化物流系統的重要設施之一。發展智能agv小車代替人工運輸,將倉庫實現無人化、智能化、自動化,提高運輸效率,減少人為干預,降低安全風險,節省運輸成本,是現代倉儲運輸行業迫在眉睫的需求。本發明所涉及的沖突解決方法,適用于倉儲物流企業中的多agv運輸系統。
另外,隨著計算機技術等前沿學科的飛速發展,路徑規劃技術在agv系統運行中是不可缺少的重要組成部分。路徑規劃是指在具有障礙物的環境中,按照一定的評價標準(評價標準通常是時間或距離),尋找一條從起始狀態到目標狀態的無碰撞路徑。在本發明中,我們采用dijkstra算法計算單個任務的最短路徑。
時間窗算法是目前多agv系統中國內外學者比較認可的一種車輛之間沖突檢測的方法。因此,在本發明中,我們借助時間窗來計算多agv之間的路徑沖突,并且通過計算兩個代價函數來決定采取等待策略或二次規劃策略來解決沖突。
目前,傳統倉儲物流產業由于極度依賴人力資源并且效率低下的原因,已經逐漸被時代所淘汰,企業正逐步尋求自動化的生產模式來代替人工操作。agv作為智能運輸系統中最重要的一環,可以極大地節省人力成本,滿足于各種類型企業的倉儲運輸需求,逐漸成為企業對倉儲進行自動化升級的首選方案。同時多agv系統中的資源分配和沖突問題也是當前的研究熱點之一。本發明所設計的基于時間窗路徑規劃算法的沖突解決方法可以很好的滿足上述需求。
技術實現要素:
發明目的:針對現有技術中存在的問題,本發明提供一種提高倉儲物流企業的運輸效率,解決多agv系統的路徑規劃沖突問題,提升企業的核心競爭力的基于時間代價函數的時間窗路徑規劃沖突解決方法。
技術方案:為解決上述技術問題,本發明提供一種基于時間代價函數的時間窗路徑規劃沖突解決方法,具體步驟如下:
第一步:采用拓撲建模法對agv運行環境進行建模,得到一張有向連接圖g=(v,e),其中v代表圖中的所有節點,e代表圖中節點之間的邊,節點之間的每一條邊(u,v)都含有一個權值wuv,表示節點之間的距離;
第二步:手動添加運輸任務,并針對每個任務,采用dijkstra算法進行路徑規劃;進行路徑規劃后會得到一條最短路徑,這條路徑是由一組路段(即有向連接圖的邊)構成的集合;
第三步:根據第二步中該路段集合計算所有路段的時間窗,并檢查所有路段的時間窗是否出現沖突,如果出現沖突則進入第四步,如果沒有出現沖突則進入第六步;
第四步:重新采用dijkstra算法進行路徑規劃,并計算等待代價函數cw和二次規劃代價函數cr的數值;
第五步:比較兩個函數的值,觀察等待代價函數cw是否大于二次規劃代價函數cr,如果cw>cr此時采用等待策略的時間成本要高于采取二次規劃策略的時間成本,則小車采用二次規劃策略,按照重新規劃的路徑進行行駛,如果cw≤cr則此時二次規劃策略的時間成本較高,則小車采取等待策略并進入第六步;
第六步:按照原路徑行駛并結束。
進一步的,所述等待代價函數cw主要由等待時間代價cw1、剩余路徑代價cw2、剩余路徑沖突代價cw3三個分量構成,并且cw=cw1+cw2+cw3:
其中等待時間代價cw1的計算方法如下
cw1=tw
其中,tw表示小車在執行任務過程中遇到沖突的等待時間;當小車由于沖突等待在某處時,運輸任務完成的時間隨之延遲,該等待時間可以通過時間窗向量事先獲得,等待的時間越長,則采取等待策略的代價越高。
剩余路徑代價cw2的計算方法如下
其中,|ej|表示剩余路徑中邊ej的距離,m表示剩余路徑中起始邊的編號,n表示剩余路徑中終止邊的編號,v表示小車的行駛速度;剩余路徑代價表示小車在繼續等待一段時間后,按照原先規劃的路徑行駛時所花費的時間,當小車剩余的路徑越少,則采取等待策略的代價越低。
剩余路徑沖突代價cw3的計算方法如下
其中,tj表示小車在行駛剩余路徑的過程中在邊ej的沖突代價,m表示剩余路徑中起始邊的編號,n表示剩余路徑中終止邊的編號;如果在邊ej未發生沖突,則tj的值為0。剩余路徑沖突代價表示小車如果不采取二次規劃策略,在等待一段時間之后按照剩余路徑行駛時,在剩余路徑中與其他小車發生沖突進行等待的時間總和。如果與其余小車的沖突越多,則等待代價越高。
進一步的,所述二次規劃代價函數cr包含二次規劃后的路徑代價cr1和二次規劃后的路徑沖突代價cr2兩個分量,并且cr=cr1+cr2:
其中二次規劃后的路徑代價cr1的計算方法如下
其中,|ek|表示二次規劃路徑中邊ek的距離,p表示二次規劃路徑中起始邊的編號,q表示二次規劃路徑中終止邊的編號,v表示小車的行駛速度;如果對小車進行二次規劃路徑,則會得到新路徑的邊序列,當新生成的路徑距離越長,則完成運輸任務所需的時間越長。
二次規劃后的路徑沖突代價cr2的計算方法如下
其中,tk表示小車在行駛二次規劃路徑的過程中在邊ek的沖突代價,p表示二次規劃路徑中起始邊的編號,q表示二次規劃路徑中終止邊的編號。需要注意的是,如果在邊ek未發生沖突,則tk的值為0。沖突代價表示小車采取二次規劃策略后,新生成的路徑與其余小車的沖突情況。如果與其余小車的沖突越多,則完成運輸任務所需的時間越長。
與現有技術相比,本發明的優點在于:
本發明針對多agv路徑規劃中的沖突問題,通過設置兩個代價函數,對于兩種常用的沖突解決策略——等待策略和二次規劃路徑策略進行了量化分析,將沖突的代價轉換為時間成本,從而選擇代價較小的策略解決沖突。本發明可以有效提高多agv系統在路徑規劃方面的運行效率,對倉儲物流企業的agv系統化部署有著重要的意義。
附圖說明
圖1為本發明的總體流程圖;
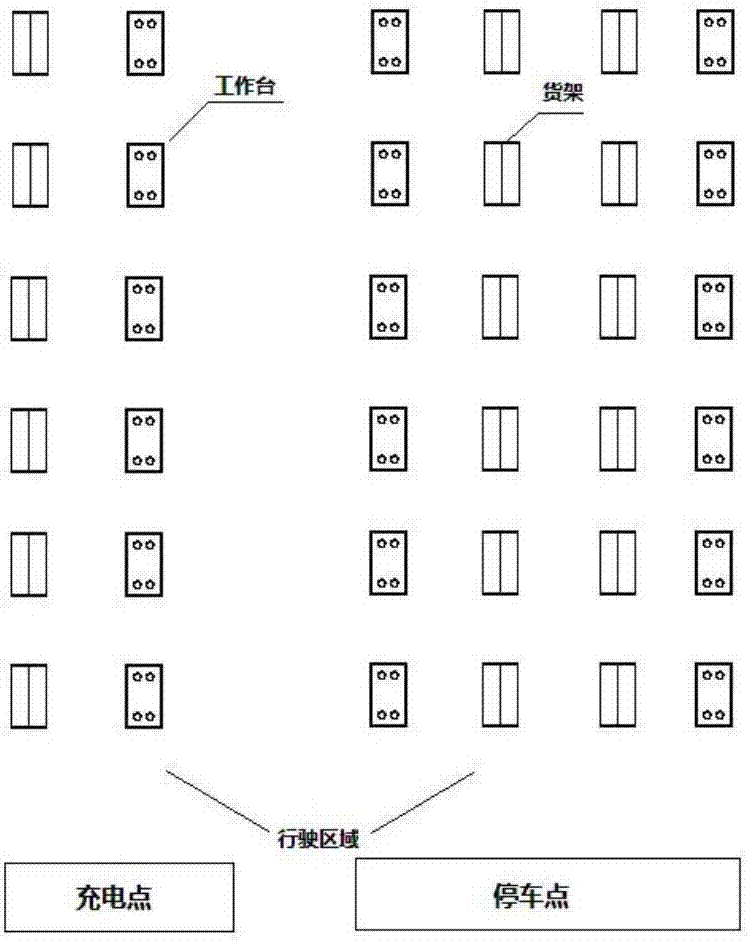
圖2為具體實施例中工廠倉庫agv工作區域平面圖;
圖3為具體實施例中agv工作區域地圖模型圖;
圖4為具體實施例中dijkstra算法的節點連接圖;
圖5為具體實施例中時間窗沖突示意圖;
圖6為具體實施例中采取停止等待策略解決時間窗沖突示意圖。
具體實施方式
下面結合附圖和具體實施方式,進一步闡明本發明。
agv、路徑規劃算法。agv又名自動運輸車,是現代智能化物流企業的重要設備之一,是本發明相關算法的運行實體;路徑規劃算法在agv運輸系統中起到了舉足輕重的作用,是agv完成運輸任務不可缺少的重要組成部分,在本發明中,我們首先采取dijkstra算法對單臺agv進行路徑規劃,為其規劃一條最短路徑,隨后運用時間窗算法對多臺agv之間的路徑沖突進行檢測,進而采取本發明提出的兩個代價函數對相關代價進行數值上的比較,然后選擇時間成本較低的策略解決路經過沖突。
1agv運行環境的建模
在使用本系統前,需要對agv運行環境進行建模,本發明選擇拓撲法進行建模,選取企業倉庫中的若干特定點與點之間可通行的路徑,將其抽象為計算機科學中常用的圖結構,用節點和弧邊的方式表示整個運行環境。本發明對于建立的模型描述如下:在有向連接圖g=(v,e)中(其中v代表圖中的所有節點,e表示圖中節點之間的邊),它的每一條邊(u,v)都含有一個權值wuv,表示節點之間的距離。圖2和圖3分別表示了工廠倉庫agv工作區域和通過拓撲法建模所得的agv工作區域地圖模型,其中紅色的連線表示連接節點的弧邊,即agv可以行使的區域。
2單臺agv路徑規劃算法
當建立完相關模型后,可以對單臺agv運用相關路徑規劃算法指導其執行運輸任務。本發明采用dijkstra算法對單個任務進行路徑規劃,在帶權值有向圖g=(v,e)中,把圖中節點的集合v分成兩組,第一組為已經求出最短路徑的頂點集合(用s表示),初始化時s中只有一個節點,即源點,以后每求出一個點的最短路徑,就將該點加入到s中,直到全部頂點都加入到s中或者求出目標點的最短路徑,算法退出,第二組為其余未確定最短路徑的節點的集合(用u表示,u=v-s,即u是s相對于v的補集),按最短路徑長度依次將第二組的節點加入到s中,加入的過程中,總保持從源點v到s中各個頂點的最短路徑長度不大于v到u中任何頂點的最短路徑長度。此外,每個頂點對應一個路徑,s中的頂點的路徑就是v到此頂點的最短路徑,u中頂點的路徑,是從v到此頂點且包括s中節點作為中間節點的最短路徑長度。該算法的具體步驟為:
(1)初始時,s只包含源點,即s={v},v的距離為0。u包含除v外的其他頂點,即:u={除v外的其余頂點},若v與u中頂點u有邊,則<u,v>正常有權值,若u不是v的出邊鄰接點,則<u,v>權值為∞。
(2)從u中選取一個距離v最小的頂點k,把k加入s中(該選定的距離就是v到k的最短路徑長度)。
(3)以k為新考慮的中間點,修改u中各頂點的距離;若從源點v到頂點u的距離(經過頂點k)比原來距離(不經過頂點k)短,則修改頂點u的距離值,修改后的距離值的頂點k的距離加上邊上的權。
(4)重復步驟2和3直到所有頂點都包含在s中。
由于無向圖本質上可以看成是雙向的有向圖,為了簡便說明算法,以圖4表示的無向圖為例,表1演示了從節點a搜索到圖中其他所有節點的最短路徑的算法流程。
表1dijkstra算法流程
3時間窗算法
在上文對單臺agv進行路徑規劃算法后,對于單個運輸任務,可以滿足運輸需求,但一般企業倉庫中需要多臺agv同時完成運輸任務,此時多臺agv之間的路徑可能出現重疊或者沖突,如果不采取措施,多臺agv在運行過程中可能會產生碰撞,影響整個運輸系統的穩定性,導致運輸任務延誤。本發明采取基于時間窗的多agv路徑規劃算法對多agv之間的沖突進行檢測,該算法的核心在于避免小車之間沖突與碰撞。下面通過示例對該算法的沖突檢測和解決方式進行說明。
假設現在有兩個運輸任務t1、t2需要執行,t1的優先級高于t2的優先級,兩個任務分別被分配給兩臺空閑的小車c1,c2。如果兩臺小車在執行任務的過程中在路段ej中出現沖突,則路段ej對應的時間窗向量表示為:
其中,w1j表示任務t1在路段ej的時間窗,w2j表示任務t2在路段ej的時間窗。
假設兩個時間窗分量出現重疊,則會出現圖5所示的情況
如圖所示,由于
為了解決此類沖突,一般有兩種方法:停止等待策略和二次規劃路徑策略。采用這兩種策略解決沖突有可能會產生新的沖突,需要進一步使用上述策略,直到所有小車互相都沒有沖突為止。對于停止等待策略,可以運用在上述例子中,即優先級高的小車先進入某一路段,優先級低的小車后進入,停止等待策略命令優先級低的小車在檢測到時間窗會出現沖突時,暫時不進入沖突路段,停在前一路段中,等待沖突路段的小車(即高優先級的小車)駛出該路段時再進入。在本例中,2號小車等待1號小車駛出路段ej再進入ej。通過停止等待策略解決相向沖突的示意圖如圖6所示。
圖中所示的2號小車等待一段時間,相應地,在路段ej的時間窗將往后平移,此時,路段ej的時間窗沒有沖突,兩臺小車可以先后通過該路段。
對于二次規劃路徑策略,通常用在停止等待策略無法完全解決沖突的情況中。如果兩臺小車有多個路段發生沖突,僅僅通過停止等待策略并不能完全解決沖突,反而可能導致整個系統的停滯或延誤,這時需要重新為其中一輛小車規劃路徑,通過設置沖突路段不可用來為路徑規劃算法增加限制條件,根據二次規劃出的路徑更新時間窗向量表,循環進行,直到所有小車的時間窗都不發生沖突為止。
4代價函數
通過上文可知,在agv遇到沖突時,通常有兩種策略對沖突進行解決,即停止等待策略和二次規劃路徑策略。本發明針對上述兩種策略,提出兩個分別描述其時間代價的函數,通過量化的方式比較兩種策略的時間成本,從而采取完成任務時間更短的一種策略解決沖突。下面對兩種代價函數進行詳細介紹。
當小車在運行過程中出現沖突時,小車需要根據一定的評判標準決定是否采用二次規劃策略進行路徑調整,這里就涉及到一個等待代價和二次規劃路徑代價的比較問題,本文設計了一種基于等待代價函數cw和二次規劃代價函數cr的綜合評價策略,將其應用于多臺小車的路徑規劃。
假設該策略不考慮小車的任務優先級、任務類型等因素,并且約定小車在運行過程中的行駛速度恒定不變。等待代價函數cw主要由以下三個子項構成:
(1)等待時間代價cw1。當小車由于沖突等待在某處時,運輸任務完成的時間隨之延遲,該等待時間可以通過時間窗向量事先獲得,等待的時間越長,則采取等待策略的代價越高。
cw1=tw(1)
其中,tw表示小車在執行任務過程中遇到沖突的等待時間。
(2)剩余路徑代價cw2。剩余路徑代價表示小車在繼續等待一段時間后,按照原先規劃的路徑行駛時所花費的時間,當小車剩余的路徑越少,則采取等待策略的代價越低。
其中,|ej|表示剩余路徑中邊ej的距離,m表示剩余路徑中起始邊的編號,n表示剩余路徑中終止邊的編號,v表示小車的行駛速度。
(3)剩余路徑沖突代價cw3。剩余路徑沖突代價表示小車如果不采取二次規劃策略,在等待一段時間之后按照剩余路徑行駛時,在剩余路徑中與其他小車發生沖突進行等待的時間總和。如果與其余小車的沖突越多,則等待代價越高。
其中,tj表示小車在行駛剩余路徑的過程中在邊ej的沖突代價,m表示剩余路徑中起始邊的編號,n表示剩余路徑中終止邊的編號。需要注意的是,如果在邊ej未發生沖突,則tj的值為0。
等待代價函數cw為cw1、cw2、cw3這三個代價的總和,即如果采取等待策略,完成運輸任務所需的實際時間如公式4所示:
cw=cw1+cw2+cw3(4)
如果對小車進行二次規劃,使其按照重新規劃的路徑行駛,則小車無需等待,二次規劃代價函數中沒有等待時間代價分量,只包含二次規劃后的路徑代價和二次規劃后的路徑沖突代價這兩個分量,由于設置了沖突路段不可用,則重新規劃的路徑可能會增加路徑長度,其相應的路徑代價可能有所提高。
可以得出,二次規劃代價函數cr由以下兩個子項構成:
(1)二次規劃后的路徑代價cr1。如果對小車進行二次規劃路徑,則會得到新路徑的邊序列,當新生成的路徑距離越長,則完成運輸任務所需的時間越長。
其中,|ek|表示二次規劃路徑中邊ek的距離,p表示二次規劃路徑中起始邊的編號,q表示二次規劃路徑中終止邊的編號,v表示小車的行駛速度。
(2)二次規劃后的路徑沖突代價cr2。沖突代價表示小車采取二次規劃策略后,新生成的路徑與其余小車的沖突情況。如果與其余小車的沖突越多,則完成運輸任務所需的時間越長。
其中,tk表示小車在行駛二次規劃路徑的過程中在邊ek的沖突代價,p表示二次規劃路徑中起始邊的編號,q表示二次規劃路徑中終止邊的編號。需要注意的是,如果在邊ek未發生沖突,則tk的值為0。
二次規劃代價函數cr為cr1、cr2這兩個代價的總和,即如果采取二次規劃策略,完成運輸任務所需的實際時間如公式7所示:
cr=cr1+cr2(7)
當cw>cr時,此時采用等待策略的時間成本要高于采取二次規劃策略的時間成本,則小車采用二次規劃策略,主控臺重新生成新的路徑發送給小車。當cw≤cr時,此時二次規劃策略的時間成本較高,則小車采取等待策略。
以上所述僅為本發明的實施例子而已,并不用于限制本發明。凡在本發明的原則之內,所作的等同替換,均應包含在本發明的保護范圍之內。本發明未作詳細闡述的內容屬于本專業領域技術人員公知的已有技術。
- 還沒有人留言評論。精彩留言會獲得點贊!