一種頻域下電抗器電感的獲取方法與流程

本發明屬于電抗器技術領域，更具體地，涉及一種頻域下電抗器電感的獲取方法。

背景技術：

發展高壓、特高壓輸電是我國電力工業發展的必然趨勢，特高壓、超高壓輸電對電網的安全穩定運行及電能質量提出了更高的要求。電網中的無功補償，可以改善輸電系統的穩定性，抑制系統過電壓，提高輸電能力。可控電抗器是目前在電網中應用最廣泛的無功補償裝置之一。可控電抗器是一種特殊的高壓或特高壓電抗器。通過對傳輸線路負荷的電抗進行調節來提供連續的無功補償，控制電網中的無功容量，可降低傳輸線路的損耗，同時提高傳輸的有功容量。

傳統意義上的可控電抗器有調匝式可控電抗器、調氣隙尺寸式可控電抗器、可控硅控制電抗器和飽和電抗器。而應用最為廣泛的可控電抗器有兩類：可控硅控制電抗器中的晶閘管控制電抗器、鐵芯電抗器中的磁飽和式電抗器。晶閘管控制電抗器由于功率電子的快速發展而得到廣泛應用，晶閘管控制電抗器響應速度快，技術較成熟，但是造價高、維護困難、諧波污染較嚴重，大規模的應用仍受到諸多限制；磁飽和式可控電抗器主要通過調節鐵芯的飽和程度，實現電感值的調節，原理相對簡單，造價較低，因此應用廣泛。

傳統的電抗器設計主要采用與變壓器設計類似的經驗公式法，按照給定容量依次計算主鐵芯直徑、匝電壓、匝數、漏抗、鐵芯窗高、磁閥及抽頭比等參數，最終確定電抗器主體結構。該方法借鑒了變壓器設計，因此在選取鐵芯磁密時一般取值1.5t左右，相對于變壓器而言，該磁密下不會出現過度飽和，保證了能量傳輸效率，而對于電抗器而言，其輸出可調的核心在于使得鐵芯能有線性區進入非線性區，因此該方法設計出的電抗器往往存在調節范圍不達標的問題。

隨著計算機輔助設計技術的進步，利用有限元進行電磁場計算有效的彌補了經驗公式帶來的誤差，考慮到鐵磁材料的磁導率由其磁化特性—bh曲線決定，在進入飽和后其磁導率變化具有高度非線性。在正弦穩態激勵下，鐵芯的飽和程度隨著勵磁電流變化而變化，若在一個周期內鐵芯飽和程度變化較為明顯，則表明電抗器電感存在畸變，反映在電抗器輸出電流上為，在給定勵磁電壓下輸出電流引入明顯諧波，進而表明電抗器參數不合理。若這一過程采用瞬態計算，則存在，三維模型算開銷大、耗時長的問題，若后處理后電流波形諧波含量偏高又不符合設計要求，使得參數優化過程緩慢，幾乎不可能。

對正弦穩態電路問題，利用拉普拉斯變換可將時域模型轉化為復頻域模型，在時域模型下計算一個周期為保證足夠的計算精度，可能需要100次甚至更多次的求解，而在復頻域中只需進行一次求解即可得到穩定的頻域解。鐵磁材料相對磁導率具有高度非線性，在一個時域周期內，由于磁密大小的變化，導致鐵磁材料相對磁導率變化劇烈，頻域分析只能設置線性材料屬性，無法準確反應這一高度非線性特點，因此，研究可在頻域計算下體現材料非線性特性的獲取方法能有效降低計算開銷與耗時，提高頻域下計算精度，使基于有限元計算的參數優化成為可能。

技術實現要素：

針對上述缺陷，本發明的目的在于提供一種頻域下電抗器電感的獲取方法，旨在解決現有的經驗公式法結果不準確以及有限元瞬態計算耗時長而導致難以對電抗器進行參數優化的技術問題。

為實現上述目的，本發明提供了一種頻域下電抗器電感的獲取方法，包括下述步驟：

s1根據電抗器的結構參數進行建模獲得電抗器模型，并對電抗器模型進行網格劃分處理獲得網格化的電抗器模型；

s2根據網格化的電抗器模型的介電常數和網格化的電抗器模型的第1次更新后的相對磁導率，網格化的電抗器模型周圍空氣域的相對磁導率和介電常數以及網格化的電抗器模型中繞組的正弦激勵進行頻域計算獲得第1次更新后的繞組電流以及網格化的電抗器模型第1次更新后的磁密；

s3根據網格化的電抗器模型第i次更新后的磁密以及電抗器的鐵芯的磁化特性數據獲得網格化的電抗器模型第i+1次更新后的相對磁導率；

s4根據網格化的電抗器模型介電常數和網格化的電抗器模型第i+1次更新后的相對磁導率，網格化的電抗器模型周圍空氣域的相對磁導率和介電常數以及網格化的電抗器模型中繞組的正弦激勵進行頻域計算獲得第i+1次更新后的繞組電流以及網格化的電抗器模型第i+1次更新后的磁密；

s5根據第i次更新后的繞組電流和第i+1次更新后的繞組電流獲得繞組電流相對差值，并判斷繞組電流相對差值是否小于預設值，若是，則根據第i+1更新后的繞組電流以及繞組激勵的電壓幅值獲得電抗器的等效阻值；否則，進入步驟s6；

s6判斷迭代次序i是否大于迭代次數n，若是，則終止；否則，令i＝i+1，并進入步驟s3；其中，1≤i≤n。

上述方法中，通過建立電抗器模型并對電抗器模型進行網格化處理獲得網格化的電抗器模型，根據網格化的電抗器模型介電常數和更新后的相對磁導率，網格化的電抗器模型周圍空氣域的相對磁導率和介電常數以及網格化的電抗器模型中繞組的正弦激勵獲得繞組電流以及網格化的電抗器模型磁密；以鐵芯的磁化特性數據以及網格化的電抗器模型的磁密獲得網格化的電抗器模型更新后的相對磁導率，從而獲得更新后的繞組電流以及網格化的電抗器模型更新后的磁密，并以繞組電流是否收斂作為是否終止迭代過程的條件，繞組電流收斂此時頻域計算下的整個區域內的磁場能量與瞬態磁場能量分布對應，根據收斂后的繞組電流獲得電抗器的電感值能夠真實反映電抗器的電感值，且以鐵芯磁化特性數據更新每個鐵芯單元的磁導率，當電抗器設計合理的情況下，繞組電流可以快速收斂，明顯降低計算次數。

進一步地，步驟s1中電抗器的結構參數包括鐵芯結構參數以及繞組結構參數。

進一步地，步驟s2中鐵芯結構參數包括鐵芯的截面積、鐵芯高度、鐵芯窗高和鐵芯窗寬以及鐵芯中氣隙高度；繞組結構參數包括繞組內徑、繞組外經、繞組高度以及繞組匝數。

進一步地，網格化的電抗器模型第i次更新后的相對磁導率包括每個繞組單元第i次更新后的相對磁導率和每個鐵芯單元第i次更新后的相對磁導率，且每個繞組單元第i次更新后的相對磁導率與每個繞組單元第i+1次更新后的相對磁導率相同。

進一步地，步驟s2中每個鐵芯單元第1磁更新后的相對磁導率取相同值。

進一步地，步驟s3包括如下步驟：

s31從網格化的電抗器模型第i次更新后的磁密中獲得每個鐵芯單元第i次更新后的磁密；

s32根據每個鐵芯單元第i次更新后的磁密和鐵芯的磁化特性數據進行差值處理獲得每個鐵芯單元第i+1次更新后的相對磁導率；

s33根據每個鐵芯單元第i+1次更新后的相對磁導率以及每個繞組單元第i+1次更新后的相對磁導率獲得網格化的電抗器模型第i+1更新后的相對磁導率。

本發明提供的以上技術方案，可以達到以下有益效果：

1、為了保證時域計算獲得的電抗器電感等效值的準確性，需要進行上百次的計算獲得電抗器電流值，本發明中由于利用鐵芯磁化特性數據修正鐵芯的相對磁導率分布，能夠快速實現鐵芯磁密分布穩定，繞組電流恒定，且整個區域內的磁場能量與瞬態磁場能量分布對應，用穩定后的繞組電流計算磁體等效電感值，使得頻域計算次數大大降低，縮短耗時，且所獲得的電抗器的等效阻值更精確。

2、根據繞組電流的收斂程度判斷電抗器繞組電流是否存在諧波含量，且根據電流的波動幅值可以判斷諧波含量的大小。

3、本發明提供的獲取方法可用于為電抗器參數優化設計，能夠縮短電抗器參數優化的時間。

附圖說明

圖1為本發明提供的頻域下電抗器的電感獲取方法的流程圖；

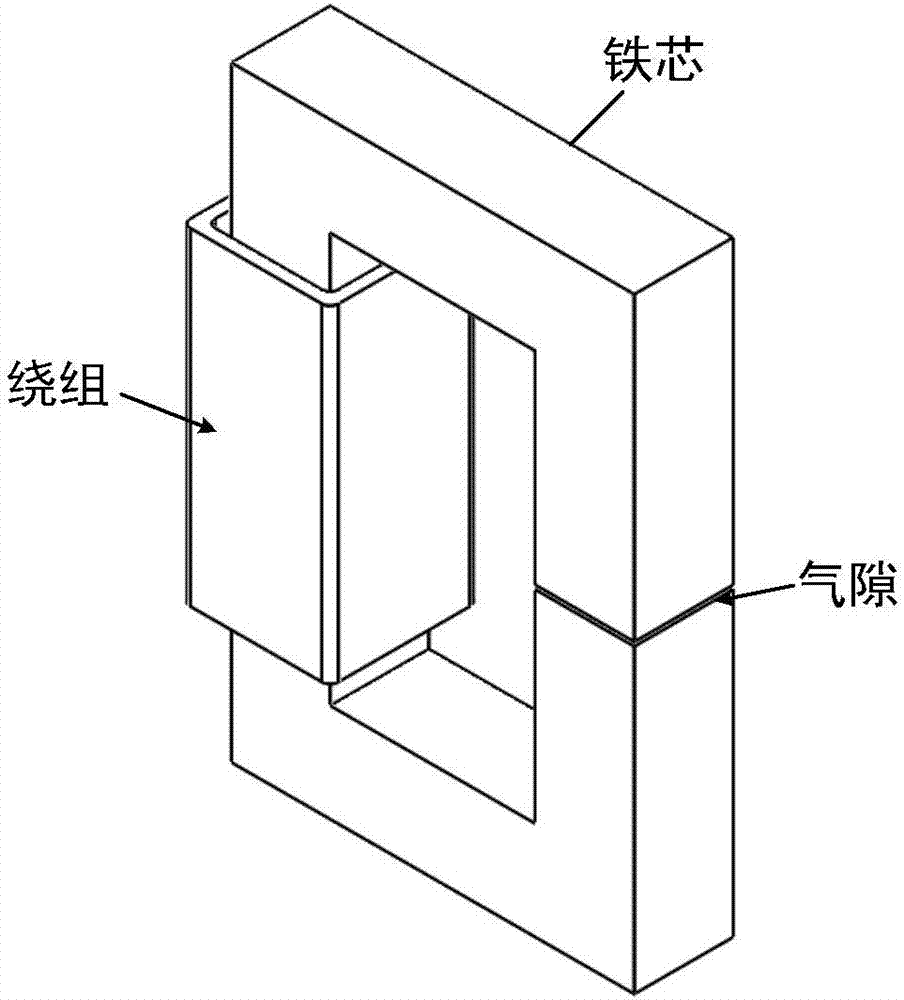
圖2為本發明提供的電抗器結構圖；

圖3為本發明提供的第一對比實施例的繞組電流以及第二對比實施例的繞組電流的對比圖；

圖4為本發明提供的第一實施例的繞組電流以及第二實施例的繞組電流的對比圖。

具體實施方式

為了使本發明的目的、技術方案及優點更加清楚明白，以下結合附圖及實施例，對本發明進行進一步詳細說明。應當理解，此處所描述的具體實施例僅用以解釋本發明，并不用于限定本發明。

圖1為本發明提供的頻域下電抗器電感的獲取方法的流程圖，包括如下步驟：

s1確定電抗器結構參數，包括鐵芯結構參數和繞組結構參數。其中，鐵芯結構參數包括鐵芯的截面積、鐵芯高度、鐵芯窗高、鐵芯窗寬以及鐵芯中氣隙高度。繞組結構參數包括繞組外徑、繞組內徑、繞組高度以及繞組匝數。

根據電抗器的結構參數進行建模獲得電抗器模型，并對電抗器模型進行網格劃分處理獲得網格化的電抗器模型；

s2根據網格化的電抗器模型的介電常數和網格化的電抗器模型的第1次更新后的相對磁導率，網格化的電抗器模型周圍空氣域的相對磁導率和介電常數以及網格化的電抗器模型中繞組的正弦激勵進行頻域計算獲得第1次更新后的繞組電流以及網格化的電抗器模型第1次更新后的磁密；

s3根據網格化的電抗器模型第i次更新后的磁密以及電抗器的鐵芯的磁化特性數據獲得網格化的電抗器模型第i+1次更新后的相對磁導率；

s4根據網格化的電抗器模型介電常數和網格化的電抗器模型第i+1次更新后的相對磁導率，網格化的電抗器模型周圍空氣域的相對磁導率和介電常數以及網格化的電抗器模型中繞組的正弦激勵進行頻域計算獲得第i+1次更新后的繞組電流以及網格化的電抗器模型第i+1次更新后的磁密；

s5根據第i次更新后的繞組電流和第i+1次更新后的繞組電流獲得繞組電流相對差值，并判斷繞組電流相對差值是否小于預設值，若是，則根據第i+1次更新后的繞組電流以及繞組激勵的電壓幅值獲得電抗器的等效阻值；否則，進入步驟s6；預設值一般取0.1％～5％。

s6判斷迭代次序i是否大于迭代次數n，若是，則終止；否則，令i＝i+1，并進入步驟s3；其中，1≤i≤n。迭代次數一般取10～50次。

在給定正弦激勵下，通過迭代計算鐵芯區域的相對磁導率分布，使得最終磁密分布穩定，繞組電流恒定，磁體等效電感值穩定，此時頻域計算下的整個區域內的磁場能量與瞬態磁場能量分布對應，若鐵芯瞬態過程中不存在過飽和區，則在頻域獲取過程中，繞組電流可快速收斂；若鐵芯瞬態過程中存在過飽和區，則繞組電流存在諧波，表明該組結構參數電抗器性能不佳，在頻域獲取中表現為電流經過幾次迭代后將呈現交替波動現象，因此可通過頻域電流的收斂性來判定電抗器結構參數。若結構參數合理，頻域下的磁能分布可視為瞬態計算的等效磁能分布。通過判斷頻域下電流的收斂性來判斷參數是否合理以及最終等效電感，通過磁芯的磁化特性數據對鐵芯的磁導率分布進行修正，能夠快速實現電感電流收斂或呈交替波動現象，相比瞬態計算次數大大減少，同時能夠判斷參數的合理性。

本發明提供的頻域下電抗器的電感獲取方法的第一實施例，其具體實現步驟為：

s1電抗器基本結構如圖2所示，電抗器結構參數中鐵芯結構參數為：鐵芯截面積120×120mm²，鐵芯窗高500mm，鐵芯窗寬250mm，鐵芯間氣隙高度1mm。電抗器結構參數中繞組結構參數工作繞組匝數為100匝，繞組外徑為180×180mm²、繞組內徑為150×150mm²、繞組高度為400mm。

在ansysmultiphysics中建立根據電抗器結構參數建立電抗器模型，對電抗器模型進行網格劃分處理獲得網格化后的電抗器模型。

s2設置每個繞組單元的相對磁導率設為1，設置每個繞組單元的介電常數為1，設置每個鐵芯單元初始相對磁導率相同，設置為鐵芯處于線性區時的平均磁導率10000，每個鐵芯單元的介電常數為1，空氣域的介電常數為1以及空氣域的磁導率設為1，設置繞組激勵為電壓激勵，繞組電壓有效值為380v，電壓激勵的頻率為50hz。

對上述網格化后的電抗器模型進行頻域計算，獲得第1次更新后繞組電流和以及網格化的電抗器模型第1次更新后的磁密。

s3利用matlab軟件調用ansysmultiphysics的第i次頻域計算結果讀取每個鐵芯單元的第i次更新后的磁密，按照每個鐵芯單元編號分別寫入數據表中，記為“編號-磁密”數據表；利用matlab根據讀出的每個鐵芯單元第i次更新后的磁密，在磁化特性數據中進行插值處理，每個鐵芯單元第i+1次更新后的相對磁導率，按照鐵芯單元編號生成對應的數據表，記為“編號-第i+1次更新后的相對磁導率”數據表。

s4根據“編號-第i+1次更新后的相對磁導率”數據表，利用ansysmultiphysics設置材料屬性命令將對應第i+1次更新后的相對磁導率寫入鐵芯單元，每個繞組單元的相對磁導率以及空區域的磁導率均保持不變。每個鐵芯單元介電常數、每個繞組單元的介電常數以及空氣域的介電常數保持不變。設置繞組激勵為電壓激勵，繞組電壓有效值為380v，電壓激勵的頻率為50hz。進行第i+1次頻域計算，獲得第i+1更新后的繞組電流ii+1以及網格化的電抗器模型第i+1次更新后的磁密。

s5判斷繞組電路是否收斂，根據公式err＝|ii+1-ii|/ii×100％獲得繞組電流的相對差值，其中，ii為第i次更新后的繞組電流，ii+1為第i+1次更新后的繞組電流，若繞組電流的相對差值err<1％，認為已經收斂，此時的磁導率分布能夠充分反映鐵芯的非線性特性，否則，進入步驟s5。

s6判斷迭代次序i是否大于迭代次數10，若是，則終止，否則，令i＝i+1，并進入步驟s3。

本發明提供的頻域下電抗器的電感獲取方法的第二實施例，包括如下步驟：

s1電抗器基本結構如圖2所示，電抗器結構參數中鐵芯結構參數為：鐵芯截面積120×120mm²，鐵芯窗高500mm，鐵芯窗寬250mm，鐵芯間氣隙高度5mm。電抗器結構參數中繞組結構參數工作繞組匝數為100匝，繞組外徑為180×180mm²、繞組內徑為150×150mm²、繞組高度為400mm。

在ansysmultiphysics中建立根據電抗器結構參數建立電抗器模型，對電抗器模型進行網格劃分處理獲得網格化后的電抗器模型。

s2對網格化的電抗器模型的第1次相對磁導率和介電常數設置以及對網格化的電抗器模型周圍空氣域的相對磁導率設置與第一實施例中步驟s2相同，設置繞組激勵為電壓激勵，繞組電壓有效值為220v，電壓激勵的頻率為50hz。

s3中對網格化的電抗器模型第i次更新后的相對磁導率和介電常數設置以及對網格化的電抗器模型周圍空氣域的相對磁導率設置與第一實施例中步驟s3相同。設置繞組激勵為電壓激勵，繞組電壓有效值為220v，電壓激勵的頻率為50hz。進行第i+1次頻域計算，獲得第i+1次更新后的繞組電流i1以及網格化的電抗器模型第i+1次更新后的磁密。

步驟s4至步驟s5均與第一實施例中步驟s3至步驟s5相同。

本發明提供的第一對比實施例中，利用有限元分析軟件通過對電抗器進行有限元建模，所選擇的電抗器結構參數與第一實施例中相同，激勵為正弦激勵，電壓等效幅值以及頻率與第一實施例中相同，進行時域計算，為了精確獲得兩個周期的電抗器繞組電流，進行100次的時域計算。

本發明提供的第二對比實施例中，利用有限元分析軟件通過對電抗器進行有限元建模，所選擇的電抗器結構參數與第二實施例中相同，激勵為正弦激勵，電壓等效幅值以及頻率與第二實施例中相同，進行時域計算，為了精確獲得兩個周期的電抗器繞組電流，進行100次的時域計算。

圖3為第一對比實施例的繞組電流以及第二對比實施例的繞組電流的對比圖，第一對比實施例設置的氣隙高度較低，氣隙磁阻相對較小，在電流較低時電抗器電感較大，隨著電流的增加，鐵芯進入飽和區，電抗器電感減小，導致電流迅速增大，從而引入較高的諧波含量；第二對比實施例氣隙高度相對較高，在220v電壓下兩周期內鐵芯磁密發生變化但并未進入飽和區，因此電感穩定，電流幾乎沒有諧波。

圖4為為第一實施例的繞組電流以及第二實施例的繞組電流的對比圖，采用等效磁能分布計算電抗器電感，第一實施例中由于存在飽和區，導致最終迭代結果沒有達到收斂條件，而第二實施例中可快速收斂，且電感值與瞬態計算一致，計算量大大降低。由于且從第一實施例以及第二實施例可以看出，由于根據讀出的每個鐵芯單元磁密，在磁化特性曲線中進行插值，求解對應的更新后的相對磁導率，以更新后的相對磁導率采用頻域計算獲得更新后的繞組電流，快速實現每個鐵芯單元的相對磁導率穩定，繞組電流快速穩定，將計算次數保持在10次。

對比圖3和圖4，可以得出：當采用頻域下等效磁能分布法計算電抗器電感時，輸出電流穩定表明電抗器結構參數合理，瞬態電流幾乎沒有諧波；當輸出電流不穩定，無法收斂時表明電抗器結構參數不合理，瞬態電流諧波含量較高，在參數優化時，可根據頻域下的收斂性來判斷參數是否合理。

綜上可以得知，本發明提供的獲取方法，可在保證精度的同時大大減少計算量，且能夠根據收斂性排除不合理參數，解決了經驗公式法結果不準確、瞬態計算法計算量大無法應用于參數優化的問題。

本領域的技術人員容易理解，以上所述僅為本發明的較佳實施例而已，并不用以限制本發明，凡在本發明的精神和原則之內所作的任何修改、等同替換和改進等，均應包含在本發明的保護范圍之內。