一種基于勒讓德傅立葉多項式的圓柱干涉拼接方法和系統與流程
本發明涉及光學三維測量領域,尤其涉及一種基于勒讓德傅立葉多項式的圓柱干涉拼接方法。
背景技術:
在現代工業中,精密軸類零件是機器設備中的重要組成部分,如精密機床的回轉軸及空氣靜壓軸承,精密陀螺中的氣浮軸承、動壓馬達等。精密軸類零件的面形誤差直接影響到精密設備的使用性能。因此,需要對精密軸類零件檢測,獲取它們的面形誤差,為零件的加工誤差分析及工藝提供指導,保證軸類零件的質量。
目前,針對精密軸類零件的面形誤差檢測,主要采用接觸式測量方法,如三坐標測量機和圓柱度儀。然而,接觸式測量方法的采樣率低,難以獲得高分辨率的測量結果,用于表征待測圓柱的360度面形誤差分布。此外,接觸式探針容易磨損,會產生測量誤差,影響最終的測量結果。干涉測量術,作為光學三維測量技術的分支,由于具有非接觸性、全場性、高精度、高分辨率等特點,使其在精密零件、光學元件的面形誤差檢測等領域得到了日益廣泛的應用。
由于大口徑、低F/數的參考鏡制造存在困難,使得干涉術還存在解決大空間尺寸物體、大數值孔徑(或低F/數)、高分辨率及特殊形狀物體(如球面、柱面等)的面形測量等方面的難題。干涉拼接術為解決這類問題提供了新思路。它的基本原理是將被測物體劃分為若干個小尺寸的子孔徑,相鄰的子孔徑間有局部重疊區,每次用小口徑的干涉系統測量待測物體的局面面形,通過移動、轉動待測物體或干涉系統,測得全部子孔徑面形,然后采用拼接術得到全孔徑的測量結果。文獻(J.Peng,H.Xu,Y.Yu,and M.Chen,“Stitching interferometry for cylindrical optics with large angular aperture,”Meas.Sci.Technol.,vol.26,no.2,p.25204,2015.)借鑒了干涉拼接術的基本思想,獲得了大數值孔徑柱面光學元件的全口徑面形誤差。然而,現有干涉拼接算法要求相鄰的子孔徑間有局部重疊區,因此子孔徑數目較多,測量時間長。此外,為了實現拼接,需要查找重疊區內的對應點對,而調整機構的運動誤差會引起點匹配誤差,拼接過程需要采用迭代法消除點的匹配誤差,導致拼接算法復雜。因此,如何提供一種高效、便捷的圓柱干涉拼接方法成為精密檢測領域中的一項技術難題,亟待解決。
技術實現要素:
有鑒于此,本發明的目的在于提供一種基于勒讓德傅立葉(Legendre-Fourier)多項式的圓柱干涉拼接方法,旨在解決現有圓柱干涉拼接測量中需要重疊區、測量時間長;需要查找重疊區內的對應點,拼接算法復雜的問題。
本發明提出一種基于勒讓德傅立葉多項式的圓柱干涉拼接方法,主要包括:
步驟一、利用柱面干涉測量系統獲取待測圓柱的子孔徑測量數據;
步驟二、根據所述子孔徑測量數據,分離測量數據中的失調像差,獲得子孔徑面形數據;
步驟三、定義局部坐標系和全局坐標系,將所述的子孔徑面形數據變換成全局三維坐標。
步驟四、利用勒讓德傅立葉多項式擬合所述的全局三維坐標,所得擬合結果即為待測圓柱的360度面形誤差分布。
另一方面,本發明還提供一種基于勒讓德傅立葉多項式的圓柱干涉拼接系統,所述系統包括:
子孔徑數據獲取模塊,用于利用柱面干涉測量系統獲取待測圓柱的子孔徑測量數據;
失調像差分離模塊,用于通過二維Legendre多項式(V.N.Mahajan,“Orthonormal aberration polynomials for anamorphic optical imaging systems with rectangular pupils,”Appl.Opt.,vol.49,no.36,pp.6924–6929,2010.)分離所述子孔徑數據中的失調像差,獲得子孔徑面形數據;
坐標轉換模塊,用于定義局部坐標系和全局坐標系,將所述的子孔徑面形數據轉換成全局三維坐標;
拼接模塊,用于通過勒讓德傅立葉多項式同時擬合所述的全局三維坐標數據,獲得待測圓柱的360度面形誤差分布。
本發明提供的技術方案與現有干涉拼接技術相比,其顯著優點包括:(1)本發明無需相鄰的子孔徑有局部重疊區,能夠減少測量所需子孔徑的數目,縮短測量時間;(2)本發明無需計算重疊區內的對應點,能夠降低拼接算法的復雜性。
附圖說明
圖1為本發明一實施方式中基于勒讓德傅立葉多項式的圓柱干涉拼接方法流程圖;
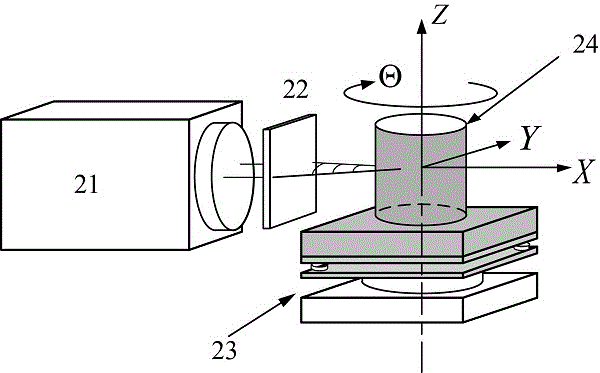
圖2為本發明一實施方式中柱面干涉測量系統的示意圖;
圖3為本發明一實施方式中基于勒讓德傅立葉多項式的圓柱干涉拼接系統30的內部結構示意圖;
圖4為本發明一實施方式中相鄰子孔徑間沒有重疊區,利用柱面干涉系統對金屬軸檢測時獲取的子孔徑的測量結果;
圖5為本發明一實施方式中利用基于勒讓德傅立葉多項式的拼接算法獲得待測金屬軸的360度面形誤差分布圖;
圖6為本發明一實施方式中相鄰子孔徑間具有局部重疊區,利用柱面干涉系統對金屬軸檢測時獲取的子孔徑的測量結果;
圖7為本發明一實施方式中利用重疊干涉拼接算法獲得待測金屬軸的360度面形誤差分布圖。
具體實施方式
為了使本發明的目的、技術方案及優點更加清楚明白,以下結合附圖及實施例,對本發明內容進一步詳細說明。應當理解,此處所描述的具體實施例僅用以解釋本發明,并不用于限定本發明。
本發明采用如下技術方案:首先利用柱面干涉測量系統獲取待測圓柱的子孔徑測量數據;其次利用二維Legendre多項式分離測量結果中的失調像差,獲得子孔徑面形數據;接著定義局部坐標系和全局坐標系,將所述的子孔徑面形數據轉換成全局三維坐標數據;最后利用勒讓德傅立葉多項式擬合全局三維坐標數據,即可獲得待測圓柱的360度面形誤差分布。這種方法無需要求相鄰的子孔徑間局部重疊,只需緊密連接,能夠減少子孔徑的數目,縮短測量時間;無需查找重疊點對,能夠降低拼接算法的復雜性。
以下將對本發明所提供的一種基于勒讓德傅立葉多項式的圓柱干涉拼接方法進行詳細說明。
請參閱圖1,為本發明一實施方式中基于勒讓德傅立葉多項式的圓柱干涉拼接測量方法流程圖。
在步驟S1中,步驟一、利用柱面干涉測量系統獲取待測圓柱的子孔徑測量數據。
在本實施方式中,所述的柱面干涉測量系統,請參閱圖2,由平面干涉儀21,柱面波轉換器22,多自由度的調整工作臺23和待測圓柱24組成。它的工作原理是:柱面波轉換器將干涉儀發出的平面波轉換成理想柱面波前,經待測圓柱面反射后攜帶有面形誤差信息再次經過柱面波轉換器變成近似平面波,最后返回到干涉儀內部與參考波前干涉。通過解調干涉儀記錄的條紋圖即可獲得待測柱面的面形誤差。
在本實施方式中,所述步驟一具體包括:
根據柱面波轉換器的F/數和通光孔徑將待測圓柱劃分成若干子孔徑,并規劃測量路徑。
根據測量路徑調整待測圓柱,使每個子孔徑在測量時的條紋數最少,即滿足零位干涉測量條件,并利用柱面干涉測量系統獲取每個子孔徑測量數據。
在步驟S2中,步驟二、分離子孔徑測量數據中的失調像差,獲得子孔徑面形數據。
在本實施方式中,所述步驟二具體包括:
利用二維Legendre多項式擬合子孔徑測量數據,其中W表示擬合的相位數據,ai表示多項式的系數,Li表示二維Legendre多項式的基函數,i=1,…,N表示多項式的項數,ii為多項式的階數,ii∈[7,15]。對于一般的光學系統,面形誤差的高階分量不會太大,使用7階Legendre多項式擬合的誤差小于0.01。二維Legendre多項式的階數在理論上可以取值為很大,但是取值越大,求解時占用的內存越多,時間成本也越高,因此,在本實施例中,ii=7。然后利用公式其中Wm表示子孔徑測量數據,分離測量結果中的失調像差,獲得子孔徑面形數據Wr。
在步驟S3中,步驟三、定義局部坐標系和全局坐標系,根據柱面波轉換器的參數和待測圓柱的名義運動量將所述的子孔徑面形數據轉換成全局三維坐標數據。
在本實施方式中,所述步驟三具體包括:
定義局部坐標系,坐標原點位于柱面波轉換器的中心,利用公式將子孔徑面形數據(u,v,Wr)轉換成局部三維坐標(z,θ,Δr),其中,s為比例縮放因子,d表示柱面波轉換器上下兩個標志點之間的距離,dp表示這兩個標志點的像素坐標差;rbf表示柱面波轉換器的后焦距,u和v表示像素坐標,z表示沿著圓柱軸線方向的坐標,θ表示角度坐標,Δr表示待測圓柱的徑向誤差。
定義全局坐標系,Z軸與待測圓柱的中心線重合,根據圓柱的名義轉動參數θ0和移動參數z0,利用公式將局部三維坐標(z,θ,Δr)轉換成全局三維坐標(Z,Θ,Δr)。
在步驟S4中,利用勒讓德傅立葉多項式擬合所述的全局三維坐標數據,即可獲得待測圓柱的360度面形誤差分布。
在本實施方式中,所述步驟四具體包括:
建立兩個行數相等的矩陣Mk和Mc,分別用于表示各子孔徑相對基準子孔徑的位置偏差和待測圓柱的360度面形誤差,
其中Npx表示單個子孔徑所對應的像素點數,Ns表示完成圓柱的360度面形測量所需要的子孔徑數目,(Npx,Ns)第Ns個子孔徑的第Npx個像素點。LFn,m表示勒讓德傅立葉多項式的基函數:
n=0,…,jj,jj表示勒讓德傅立葉多項式的階數,jj∈[5,10]。對于高精度的圓柱面形誤差,5階多項式就能保證足夠的擬合精度。勒讓德傅立葉多項式的階數在理論上取值可以為很大,然而取值越大,矩陣Mc的列數越大,占用的內存越多,因此,在本實施例中,jj=5。
建立如下方程
ΔR=MA
其中ΔR=[Δr(1,1),…,Δr(Npx,Ns)]T,M=[Mc,Mk],A為系數矩陣。將所有像素點對應的全局三維坐標(Z,Θ,Δr)代入到上述公式中構建線性方程組,然后求解上述方程組獲得系數矩陣A的值,最后將矩陣Mc與其對應的系數相乘,獲得待測圓柱的360度面形誤差分布。
本發明提供的一種基于勒讓德傅立葉的圓柱干涉拼接方法,首先通過柱面干涉測量系統獲取待測圓柱的子孔徑測量數據;然后利用二維Legendre多項式分離測量結果中的失調像差,獲得子孔徑面形數據;接著定義局部坐標系和全局坐標系,將子孔徑面形數據轉換成全局三維坐標數據;最后利用勒讓德傅立葉多項式擬合全局三維坐標數據,即可獲得待測圓柱的360度面形誤差分布。這種方法無需相鄰子孔徑間有局部重疊區,能夠減少子孔徑的數目,縮短測量時間;無需查找重疊區內的對應點,能夠降低拼接算法的復雜性。
以下將對本發明所提供的一種基于勒讓德傅立葉的圓柱干涉拼接系統進行詳細說明。
圖3所示為本發明一實施方式中基于勒讓德傅立葉的圓柱干涉拼接系統30的結構示意圖。
在本實施方式中,基于勒讓德傅立葉的圓柱干涉拼接系統30,主要包括子孔徑數據獲取模塊31、失調像差分離模塊32、坐標轉換模塊33以及拼接模塊34。
子孔徑數據獲取模塊31,用于利用柱面干涉測量系統獲取待測圓柱的局部測量數據。
在本實施方式中,所述子孔徑數據獲取模塊31具體用于:
●根據柱面波轉換器的F/數和通光孔徑將待測圓柱劃分成若干子孔徑,并規劃測量路徑。
●根據測量路徑調整待測圓柱,使每個子孔徑在測量時的條紋數最少,即滿足零位干涉測量條件,并利用柱面干涉測量系統獲取每個子孔徑測量數據。
失調像差分離模塊32,用于通過二維Legendre多項式,分離子孔徑測量結果中的失調像差。
在本實施方式中,所述失調像差分離模塊32具體用于:
利用二維Legendre多項式擬合子孔徑測量數據,其中W表示擬合的相位數據,ai表示多項式的系數,Li表示Legendre多項式的基函數,i=1,…,N表示多項式的項數,ii為二維Legendre多項式的階數,ii∈[7,15]。對于一般的光學系統,面形誤差的高階分量不會太大,使用7階Legendre多項式擬合的誤差小于0.01。另一方面,二維Legendre多項式的階數越高,求解時占用的內存越多。因此,在本實施例中,ii=7。
然后利用公式其中Wm表示子孔徑測量數據,即可分離測量數據中的失調像差,獲得子孔徑面形數據Wr。
坐標轉換模塊33,用于定義局部坐標系和全局坐標,根據柱面波轉換器和待測圓柱的名義運動量將所述的子孔徑面形數據轉換成全局三維坐標。
在本實施方式中,所述坐標轉換模塊33具體用于:
●定義局部坐標系,坐標原點位于柱面波轉換器的中心,利用公式將子孔徑面形數據(u,v,Wr)轉換成三維坐標(z,θ,Δr),其中,s為比例縮放因子,d表示柱面波轉換器上下兩個標志點之間的距離,dp這兩個標志點的像素坐標差;rbf表示柱面波轉換器的后焦距,u和v表示像素坐標,z表示沿著圓柱軸線方向的坐標,θ表示角度坐標,Δr表示待測圓柱的徑向誤差。
●定義全局坐標系,Z軸與待測圓柱的中心線重合。根據圓柱的名義轉動參數θ0和移動參數z0,利用公式將局部三維坐標(z,θ,Δr)轉換成全局三維坐標(Z,Θ,Δr)。
拼接模塊34,用于利用勒讓德傅立葉多項式擬合全局三維坐標數據,獲得待測圓柱的360度面形誤差分布。
在本實施方式中,所述拼接模塊34具體用于:
●建立兩個行數相等的矩陣Mk和Mc,分別用于表示各子孔徑相對基準子孔徑的位置偏差和待測圓柱的360度面形誤差,
其中Npx表示單個子孔徑所對應的像素點數,Ns表示完成圓柱的360度面形測量所需要的子孔徑數目,(Npx,Ns)第Ns個子孔徑的第Npx個像素點。LFn,m表示勒讓德傅立葉多項式的基函數:
n=0,…,jj,jj為勒讓德傅立葉多項式的階數,jj∈[5,10]。對于高精度的圓柱面形誤差,5階多項式就能保證足夠的擬合精度;另一方面,勒讓德傅立葉多項式的階數越高,矩陣Mc的列數越大,求解時占用的內存越多。本實施例中,jj=5。
建立如下方程
ΔR=MA
其中ΔR=[Δr(1,1),…,Δr(Npx,Ns)]T,M=[Mc,Mk],A為系數矩陣。將所有像素點對應的全局三維坐標(Z,Θ,Δr)代入到上述公式中構建線性方程組,然后求解上述方程組獲得系數矩陣A的值,最后將矩陣Mc與其對應的系數相乘,即可獲得待測圓柱的360度面形誤差分布。
本發明提供的一種基于勒讓德傅立葉的圓柱干涉拼接系統30,測量時相鄰的子孔徑間無需局部重疊,只需緊密連接,能夠減少測量所需子孔徑的數目,縮短測量時間;無需查找重疊區內的對應點,能夠降低拼接算法的復雜性。
為了測試基于勒讓德傅立葉的圓柱干涉拼接方法的有效性,對一金屬圓柱測量。首先根據柱面波轉換器的F/數和通光孔徑劃分子孔徑,并規劃測量路徑。圖4為去除失調像差之后的子孔徑相位圖,由于不需要重疊掃描,所以只需18個子孔徑即可完成待測金屬圓柱的360度面形測量。隨后采用本發明所提方法擬合所有子孔徑的相位,獲得待測金屬圓柱的360度面形誤差分布,如圖所5所示。
為了與現有干涉拼接方法比較,測量過程中相鄰子孔徑間有局部重疊區,利用重疊區內對應點對計算相鄰子孔徑間的相對位置偏差,最后根據計算結果采用坐標變換方法消除重疊區的相位差,獲得待測圓柱的360度面形誤差分布。由于所搭建柱面干涉測量系統的測量視角為18.9度,如前文所述,為了保證實現重疊拼接,擬采用36子孔徑完成待測圓柱的360度面形測量。因此,相鄰子孔徑間的重疊角度約為8.9度。圖6為在各個子孔徑位置記錄的干涉圖和相位圖,圖7為采用重疊拼接法獲得的360度面形誤差分布。比較圖5和圖7的結果可知,本發明所提方法與重疊拼接方法獲得結果基本一致,但采用本發明所用方法無需相鄰子孔徑有局部重疊區,能夠顯著減少子孔徑的數目,縮短測量時間。此外,由于采用最小二乘擬合算法直接擬合測量數據,只需將子孔徑數據變換到全局坐標系下,無需要確定重疊區內的對應點對,能夠降低拼接算法的復雜性。
值得注意的是,上述實施例中,所包括的各個單元只是按照功能邏輯進行劃分的,但并不局限于上述的劃分,只要能夠實現相應的功能即可;另外,各功能單元的具體名稱也只是為了便于相互區分,并不用于限制本發明的保護范圍。
另外,本領域普通技術人員可以理解實現上述各實施例中的全部或部分步驟是可以通過程序來指令相關的硬件來完成,相應的程序可以存儲于一計算機可讀取存儲介質中,所述的存儲介質,如ROM/RAM、磁盤或光盤等。
以上所述僅為本發明的較佳實施例而已,并不用以限制本發明,凡在本發明的精神和原則之內所作的任何修改、等同替換和改進等,均應包含在本發明的保護范圍之內。
- 還沒有人留言評論。精彩留言會獲得點贊!