一種新型光譜多元分析分類與識別方法及其用途與流程

本發明涉及光譜分析領域，可用于石化、煙草、醫藥、環境、食品檢測等領域。本發明針對SIMCA方法因歐氏距離導致分類不夠精確的問題，采用了馬氏距離來代替歐式距離進行預測，是一種改進的SIMCA方法。

背景技術：

分子光譜(紅外、近紅外和拉曼)從分子水平上反映了物質組成與結構信息,紫外，LIBS、X熒光等波譜則從電子或原子水平上反映物質組成和結構的信息。隨著光譜儀器技術的發展，這些光譜的獲取也越來越容易，不僅速度快，且大多無損，因此，光譜已經成為分析技術的理想信息載體。復雜物質光譜是其組分光譜的疊加，共存組分信息干擾使得分析難度增加，多元分析方法則是用來提取其有用信息的有力工具。將光譜和多元分析方法結合起來，稱之為現代光譜分析技術，可以實現復雜體系的定性和定量分析，具有快速、無損和高通量的等優點，已廣泛應用于石化、煙草、醫藥、環境、食品檢測等領域，對工業生產過程質量和成本控制以及流通領域質量監督等具有不可或缺的重要作用。

現代光譜分析方法包括定性和定量。其中，光譜定性分析也稱判別分析，主要用于兩個方面。一是用于判別樣品的種類，等級，來源及真偽等，二是判別待分析樣品是否落在定量分析模型范圍之內，即用于確定多元定量分析模型的適用范圍，對于保障光譜多元定量分析結果的準確性具有關鍵作用。

目前光譜多元分析中常用的分類方法主要包括：線性學習機(Linear Learning Machine)、K-最近鄰法(K-Nearest Neighbors Discrimination Method,KNN)、主成分分析(Principal Component Analysis，PCA)、馬氏距離(Mahalanobis Distance,MD)法、判別分析法(Discrimination Analysis,DA)、SIMCA方法、聚類分析、支持向量機等。在實際分析中普遍認為SIMCA方法是應用最廣和最成熟的方法，被MATLAB軟件列入工具箱，在科學研究中也是使用頻率最高的。

SIMCA方法是有監督的分類方法，分別對各類樣品光譜進行主成分分析，建立各類樣本的主成分光譜空間，分別采用主成分得分和光譜殘差信息及F檢驗構造兩個統計量T²和Q(殘差)，作為樣本分類的新屬性，然后，使用這兩個屬性計算樣本到各類樣品主成分光譜空間的歐氏距離，通過比較待測樣品到各類樣品主成分光譜空間的歐氏距離和設定閾值，實現樣本的有效分類與識別。大量光譜應用結果表明，SIMCA方法分類可以獲得很好的效果。但是，對于區分成分相近又存在著微小差異的樣本，SIMCA方法分類的效果也不理想。在光譜主成分分析分類中常用馬氏距離，以馬氏距離描述的分布在幾何學上呈橢圓狀。相比歐式距離，用馬氏距離描述實際樣本空間分布將更貼近于實際。為此，本發明提出一種改進的SIMCA新方法，采用馬氏距離來代替歐氏距離進行預測，改善SIMCA方法的分類精度。

技術實現要素：

針對SIMCA方法難以區分成分相近又存在著微小差異的樣本的問題，本發明提供了一種改進的SIMCA方法。其關鍵點在于：在SIMCA建立好模型之后，采用馬氏距離來代替歐氏距離進行預測。

本發明所述一種新型光譜多元分析分類與識別方法，包括以下步驟：

(1)樣本制備與光譜采集：收集待檢測材料，根據材料特性，將待檢測材料加工處理制成樣本，使得光譜儀能采集到樣本的光譜數據；

(2)樣本光譜數據采集與處理：用光譜儀器對步驟(1)中制得的樣本進行光譜測量，可獲得由步驟(1)制得的樣本的光譜數據組成的樣本光譜數據集Sm，，并利用SG平滑方法消除樣本光譜數據集Sm中光譜數據的高頻噪音，然后用一階求導方法消除樣本光譜數據集Sm中光譜數據的基線漂移，接著對樣本光譜數據集Sm中光譜數據進行均值中心化處理；

(3)建立多元校正模型：將經過步驟(2)處理后的樣本光譜數據集Sm分為校正集Smc和驗證集Smv，校正集Smc由具有的樣本光譜數據組成且占樣本光譜數據集Sm的光譜數據的80％；分別對校正集Smc中的每類樣本建立主成分模型，并根據Hotelling T2檢驗計算T²的臨界值根據建模樣本集的二次分布結果近似出殘差閾值Q；其中，建模樣本集的二次分布結果為校正集Smc的高斯分布結果；

(4)預測：根據主成分模型的最佳主成分數A計算驗證集Smc中樣本的T²和殘差S_i的值，通過臨界值和Q計算驗證集Smv中的樣本到主成分模型的馬氏距離，并根據最小的馬氏距離值判別待測樣本的類別；

(5)評價：以步驟(3)中所得到的驗證集Smv對不同方法預測的結果進行評價，以主成分模型的預測準確率和錯誤樣本個數為指標，評價方法的優劣，其中，預測準確率的計算公式如下：

下面對本發明進行進一步的說明：

上述方法中，在步驟(3)中，分別對校正集Smc中的每類樣本建立主成分模型，并根

據Hotelling T2檢驗計算T²的臨界值根據建模樣本集的二次分布結果近似出殘差的

閾值Q，具體步驟如下：

(3.1)對于每一個校正集Smc，將校正集Smc中樣本光譜數據按類別分開并進行編號，然后分別對每類樣本光譜數據建立PCA模型；以其中的一類光譜數據X為例，建立PCA模型：

其中為樣本均值，T為得分矩陣，P為載荷矩陣；

(3.2)用交叉驗證計算預測誤差平方加和PRESS，根據PRESS隨主成分數變化曲線確定步驟(3.1)中所建PCA模型的最佳主成分數A；

(3.3)根據步驟(3.2)中確定的最佳主成分數A建立主成分模型其中X為樣本均值，T為得分矩陣，P為載荷矩陣，E為殘差矩陣；

(3.4)根據Hotelling T2檢驗，利用步驟(3.2)中確定的最佳主成分數A，計算T²的臨

界值

(3.5)根據建模樣本集的二次分布結果，利用協方差矩陣，近似出殘差閾值Q。

上述方法中，步驟(4)具體包括如下步驟：

(4.1)根據步驟(3.2)中確定的最佳主成分數A，計算驗證集Smc中樣本的T_i²和殘差S_i的值；

(4.2)根據步驟(3.1)中T²的臨界值和殘差閾值Q，對驗證集Smv中的樣本i進行特征提取，于是樣本i可表示為

(4.3)計算樣本i到步驟(3.1)中所建PCA模型的中心(O＝{0,0})的馬氏距離；

(4.4)如果樣本i在哪一類PCA模型下得到的馬氏距離值最小，就將此樣本判為哪一類。

上述方法中，步驟(4.3)中，樣本i到步驟(3.1)中所建PCA模型的中心(O＝{0,0})的馬氏距離Dij的計算公式如下：

上述方法中，利用得分向量計算驗證集Smv中樣本i的T_i²，T_i²計算公式如下：

然后用F檢驗計算T²的臨界值

公式(4)中自由度分別為A和(n-A)，n為建模的樣本數，A為確定的最佳主成分數。

上述方法中，PCA模型的殘差閾值Q，可以用建模樣本集的二次分布結果來近似確定，殘差閾值Q計算公式如下：

其中，z_α為置信上限為100(1-α)％時的單位偏差，α的置信區間為0.04～0.06；

其中，m為樣本屬性的維度，λ_j是協方差矩陣第j個特征值；

此時，可將和作為樣本的屬性，于是可將樣本表示為Z＝{x_i|i＝1,2……m}，其中

上述方法適用于對固體、液體、氣體狀態的多組分樣品的識別。在對固體狀態的多組分樣品識別時，制備樣本時，需要將固體樣本攤開使得厚度均勻；而在對液體狀態的多組分樣品識別時，制備樣本時，需要將液體樣本充分靜置使得密度均勻；在對氣體狀態的多組分樣品識別時，制備樣本時，可將氣體狀態的多組分樣品直接充入已預先抽真空的氣體池制備成待監測樣本。

本發明具有如下有益效果：

本發明提出了一種新的光譜多元分析分類與識別方法，針對SIMCA方法區分成分相近又存在著微小差異的樣本時精度不夠的問題，分析了是因為SICMA采用了歐氏距離來預測樣本的類別。而大多的情況下，樣本分布空間具有一定的方向性和不規則性，通常不符合歐氏距離的分布。馬氏距離引進(或除以)了協方差，考慮了數據屬性的相關性，排除變量之間的干擾，在一定程度上凸顯了表達能力強的屬性。因此，本發明采用了馬氏距離代替歐氏距離來預測樣本的類別，改善SICMA方法的分類精度。

本發明可適用于固體、液體、氣體狀態的多組分樣品，例如石油類產品(如汽油，柴油等)、農產品(如糧食、茶、棉、麻、煙葉、果蔬等)、食品(如飼料、肉類、酒等)、醫藥等樣品的識別。具有應用范圍廣，精度高的特點。

附圖說明

圖1是使用馬氏距離和歐氏距離計算的樣品分布范圍。

圖2是實例1中采集的原始光譜圖。

圖3是實例1中各個類的PRESS圖和相應的T²和Q分布圖。

圖4是實例2中采集的原始光譜圖。

圖5是實例2中各個類的PRESS圖和相應的T²和Q分布圖。

具體實施方式

下面結合附圖對本發明作進一步描述。本發明實例用來解釋本發明，而不是對本發明進行限制，在本發明的精神和權利要求的保護范圍內，對本發明做出的任何修改和改變，都落入本發明的保護范圍。

實施例1

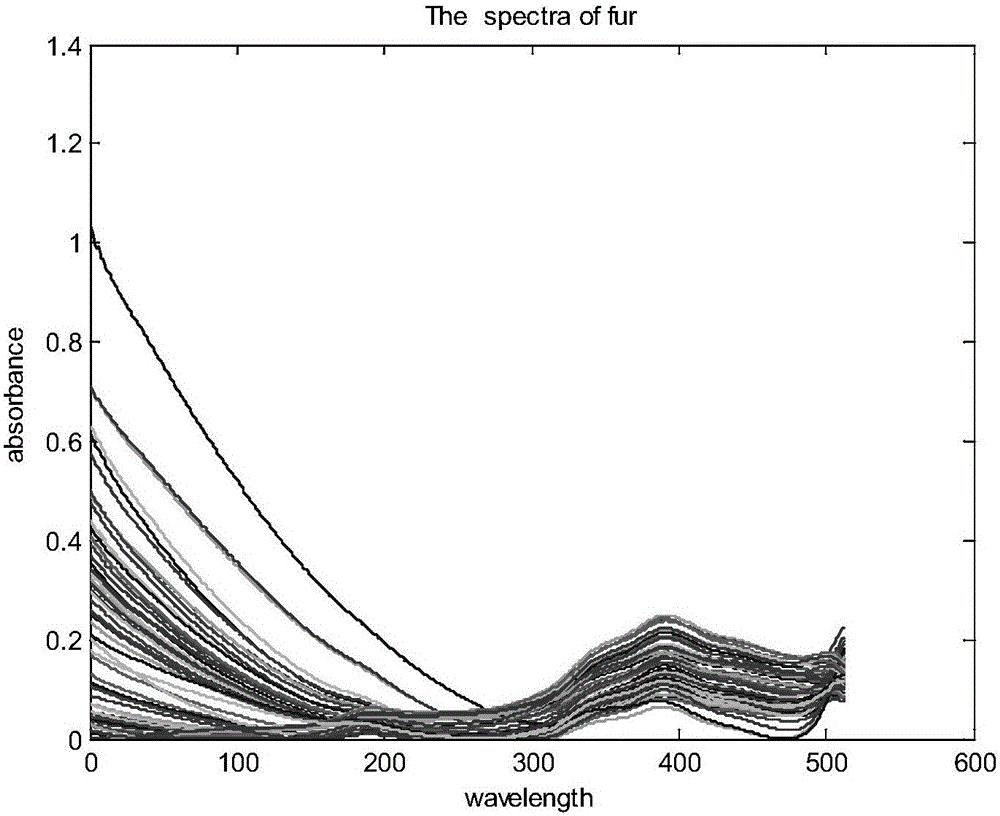
本實施案例分別為貉子，狐貍和兔子的皮毛，共76組樣本，由北京市毛麻絲織品質量監督檢驗站提供。采用HF-P12型紡織品成分分析儀(西派特(北京)科技有限公司產品)采集樣品的漫反射近紅外光譜，光譜范圍為900-1700nm，分辨率為3.1nm，積分時間100ms。以聚四氟參考板采集參比信號。將皮毛樣本平鋪在分析儀采樣平臺上，樣本用金屬砝碼壓平壓實，對每個樣品采集3張漫反射近紅外光譜譜圖，取其平均光譜為樣本光譜。圖1為皮毛樣本的原始光譜圖。

本實例實施的主要步驟如下：

1.對光譜數據采用SG平滑方法消除數據中高頻噪音，用一階求導方法消除基線漂移，然后對此光譜數據進行均值中心化處理。

2.對皮毛樣本數據集隨機劃分為校正集Smc和驗證集Smv，其中，校正集Smc和驗證集Smv分別占總樣本數的80％和20％。

3.對校正集Smc中的每類樣本建立主成分模型，用交叉驗證計算預測誤差平方加和PRESS，根據PRESS隨主成分數變化曲線確定模型的最佳主成分數A。并根據Hotelling T2檢驗計算T²臨界值根據建模樣本集的二次分布結果近似出殘差閾值Q。圖2為樣本各個類的PRESS圖和相應的T²和殘差分布圖。參考圖2,3類模型的主因子數分別確定為8，4和8。

4.根據主成分模型的最佳主成分數A計算驗證集Smv中樣本的T²和殘差S_i的值，利用T²的臨界值和殘差閾值Q，對驗證集Smv中的樣本i進行特征提取，于是樣本i可表示為

5.分別計算每一類PCA模型下樣品到模型中心(O＝{0,0})的歐氏距離。根據最小的Di值，判別待測樣本的類別。

6.分別計算每一類PCA模型下樣品到模型中心(O＝{0,0})的馬氏距離。根據最小的Di值，判別待測樣本的類別。

7.根據預測結果的準確率，評價馬氏距離和歐氏距離的分類效果。

表1為馬氏距離和馬氏距離對皮毛樣本的分類結果對比，由表中結果可知，用馬氏距離預測驗證集Smv類別的準確率明顯大于歐氏距離的。表明馬氏距離具有更強的分類與識別能力。

表1皮毛樣本分類結果對比

實施例2

食用油樣本為從北京市場上采購的橄欖油和芝麻油，模擬食用油摻假。取5ml橄欖油,分別加入不同體積的芝麻油，將樣本用振蕩器搖晃均勻，放置穩定一段時間，制備橄欖油/芝麻油比例為1％～8％的調和油，共104個樣本。將1％～4％比例范圍的調和油劃為第一類，5％～8％比例范圍的調和油劃為第二類。采用帶有ATR晶體的Agilent5500型紅外光譜儀測量樣本的紅外光譜。光譜范圍為650-4000cm^-1，分辨率為4cm^-1,掃描次數為32。以空氣為參比，用滴管吸入少量樣本滴在ATR晶體表面上，每個樣品采集3張紅外譜圖，取其平均光譜作為樣本光譜。然后使用酒精溶劑清洗ATR晶體至無樣本污染后，再采集下一個樣本的光譜。圖3為食用油的原始光譜圖。

本實例實施的主要步驟如下：

1.對光譜數據采用SG平滑方法消除數據中高頻噪音，用一階求導方法消除基線漂移，然后對此光譜數據進行均值中心化處理。

2.對于2類食用油樣本數據集，在3％～6％比例范圍內隨機選出20組樣本作為驗證集Smv，其余樣本作為校正集Smc。校正集Smc占總樣本數的80％。

3.對校正集Smc中的每類樣本建立主成分模型，用交叉驗證計算預測誤差平方加和(PRESS)，根據PRESS隨主成分數變化曲線確定模型的最佳主成分數A。并根據Hotelling T2檢驗計算T²臨界值根據建模樣本集的二次分布結果近似出殘差閾值Q。圖4為樣本各個類的PRESS圖和相應的T²和殘差分布圖。參考圖4,2類模型的主因子數分別確定為14和13。

4.根據主成分模型的最佳主成分數A計算驗證集Smv中樣本的T²和殘差S_i的值，利用T²的臨界值和殘差閾值Q，對驗證集Smv中的樣本i進行特征提取，于是樣本i可表示為

5.分別計算每一類PCA模型下樣品到模型中心(O＝{0,0})的歐氏距離。根據最小的Di值，判別待測樣本的類別。

6.分別計算每一類PCA模型下樣品到模型中心(O＝{0,0})的馬氏距離。根據最小的Di值，判別待測樣本的類別。

7.根據預測結果的準確率，評價馬氏距離和歐氏距離的分類效果。

表2為馬氏距離和馬氏距離對食用油樣本的分類結果對比，從圖4可以看出，2類的樣本基本分開，部分不同類樣本還是很接近的。說明不同類的調和油之間差別較小，分類有較大難度。由表2的分類結果可知，馬氏距離和歐氏距離都不能將樣本全部識別出來。但是，與歐氏距離相比，的分類結果明顯改善。同樣的樣本模型，歐氏距離的分類準確率為60％，而馬氏距離的準確率上升到了70％，因此馬氏距離的分類與識別能力更優。

表2食用油分類結果的對比