一種有源周期信號中有效信息提取的方法及裝置與流程
本發明涉及周期信號處理領域,更具體地,涉及一種有源周期信號中有效信息提取的方法及裝置。
背景技術:
目前,周期信號的應用非常廣泛,包括震動周期信號、電磁周期信號及機械周期信號等等。絕大多數情況下,周期信號是由一個主頻信號和許多諧波信號組成的,在實際應用中不同的構成特征反映了不同的物理意義,通過挖掘這些信號中不同頻率的特征,可以解決許多實際應用問題。但是在實際應用中,信號總是受到各種各樣的噪聲影響,當干擾復雜時,提取有效信號即高信噪比的信號會變得非常困難。
隨著人類活動區域的進一步擴大,工業的持續發展,當今所采集的電磁勘探信號中總存在著各種各樣的電磁干擾,嚴重影響了信號的信噪比,對電磁勘探的效果帶來了消極的影響。在噪聲很大時,往往只提取信號的主頻部分,或者通過經驗提取能量較大的諧波成分,有時根據經驗提取的信號是不符合質量要求的信號,沒有一種標準來指導有效數據的提取。因此急需一種針對周期信號的噪聲評價及有效信息提取的方法來指導工作和生產。
技術實現要素:
本發明提供一種克服上述問題或者至少部分地解決上述問題的。
根據本發明的一個方面,提供一種有源周期信號中有效信息提取的方法,其特征在于,包括:
S1,基于原始信號的頻率域頻譜,利用所述原始信號中有效頻率的相鄰頻率的頻譜值對所述有效頻率進行預處理,獲得預處理后的頻譜;
S2,利用離散小波變換將所述預處理后的頻譜分解為高頻成分和低頻成分;
S3,將所述高頻成分解析包絡后的高頻包絡線與所述低頻成分進行重構,獲得整體頻譜曲線的包絡線;
S4,基于整體頻譜曲線的包絡線,進行噪聲評價并提取有效信號。
進一步,所述S1進一步包括:
S1.1,利用混合基快速傅里葉變換獲得所述原始信號的頻率域頻譜;
S1.2,將所述原始信號中有效頻率的頻譜值設置為相鄰頻率的頻譜值的平均值,從而獲得預處理后的頻譜。
進一步,所述S2進一步包括:
S2.1,對所述預處理后的頻譜進行第一級離散小波變換,分解為第一低頻部分和第一高頻部分;
S2.2,對所述第一低頻部分進行第二級離散小波變換,分解為第二低頻部分和第二高頻部分;
S2.3,對所述第二低頻部分進行第三級離散小波變換,分解為第三低頻部分和第三高頻部分。
具體的,所述S1中所述高頻成分為所述第一高頻部分、所述第二高頻部分和所述第三高頻部分疊加后的高頻成分;所述低頻成分為所述第三低頻部分。
進一步,所述S3進一步包括:
S3.1,利用希爾伯特變換對所述高頻成分進行解析包絡,獲得第一包絡線;
S3.2,選取所述第一包絡線的極大值進行樣條插值,獲得所述高頻包絡線;
S3.2,將所述高頻包絡線與所述低頻成分進行重構,獲得整體頻譜曲線的包絡線。
進一步,所述S4進一步包括:
S4.1,將所述整體頻譜曲線的包絡線在有效頻率的頻譜值除以所述有效頻率的原始頻譜值,得到噪聲評價系數;
S4.2,基于所述噪聲評價系數,提取所有噪聲評價系數小于要求數值的有效頻率為所述有效信號。
具體的,S3.1中所述希爾伯特變換為:
fA(s)=f(s)+iH(f(s))
其中,f(s)為原始信號,H(f(s))為對f(s)進行希爾伯特變換得到的信號且fA(s)為希爾伯特解析信號,|fA|即為對應實數信號的上包絡曲線。
進一步,所述S4.1進一步包括:
S4.1.1,獲取所述整體頻譜曲線的包絡線在所有有效頻率的頻譜值,以及獲取所有有效頻率的原始頻譜值;
S4.1.1,基于每一個有效頻率,將所述整體頻譜曲線的包絡線在有效頻率的頻譜值除以所述有效頻率的原始頻譜值,得到每一個有效頻率的噪聲評價系數。
具體的,所述有效頻率包括主頻和諧波。
根據本發明的另一個方面,還提供一種有源周期信號中有效信息提取的裝置,包括:
預處理模塊,用于基于原始信號的頻率域頻譜,利用所述原始信號中有效頻率的相鄰頻率的頻譜值對所述有效頻率進行預處理,獲得預處理后的頻譜;
高低頻分解模塊,用于利用離散小波變換將所述預處理后的頻譜分解為高頻成分和低頻成分;
包絡線模塊,用于將所述高頻成分解析包絡后的高頻包絡線與所述低頻成分進行重構,獲得整體頻譜曲線的包絡線;
有效信號提取模塊,用于基于整體頻譜曲線的包絡線,進行噪聲評價并提取有效信號。
本申請提出一種有源周期信號中有效信息提取的方法及裝置,通過對原始信號的頻譜進行預處理后,分解為高頻成分和低頻成分,對其中的高頻成分進行二次包絡處理后再與低頻成分進行重構獲取整體信號包絡線,基于整體信號包絡線而提出后一種噪聲評價方法;利用所述噪聲評價方法,不需要進行準確計算,只需要通過估計振蕩函數的上界來估計噪聲的最大影響。應用所述噪聲評價方法,能夠得到不同頻率信號的信噪比數值,并以此提取符合生產要求的有效信號信息。本申請所述噪聲評價及提取有效信息方法可以應用于所有周期信號,尤其是對周期信號中不容易分解的非周期噪聲的影響評價具有良好的效果,可以大大的提高有效信號提取的數量和效率,具有良好的應用前景。
附圖說明
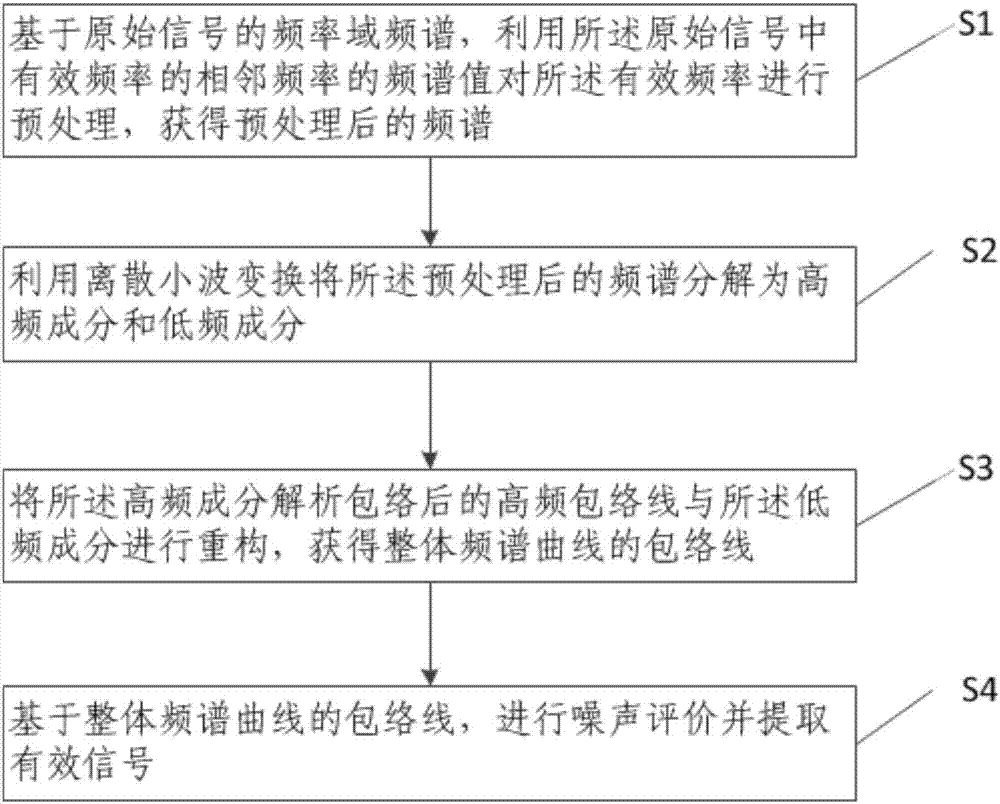
圖1為本發明一種有源周期信號中有效信息提取的方法流程圖;
圖2為本發明所述原始信號頻率域頻譜曲線示意圖;
圖3為本發明對所述原始信號頻率域頻譜預處理后的頻譜示意圖;
圖4為本發明對所述預處理后的頻譜信號進行三級小波分解的示意圖;
圖5為本發明應用三級小波分解后的高頻部分和低頻部分示意圖;
圖6為本發明基于希爾伯特變換的解析包絡理論示意圖;
圖7為本發明第一實施例高頻部分的包絡結果示意圖;
圖8為本發明第一實施例整體包絡結果示意圖;
圖9為本發明第一實施例包絡計算后包絡比例統計結果示意圖;
圖10為本發明第一實施例噪聲最大影響和實測數據的關系示意圖;
圖11為本發明第一實施例通過包絡后噪聲的估計評價數示意圖;
圖12為本發明第一實施例實際數據的包絡結果示意圖;
圖13為本發明第一實施例實際數據按5%誤差提取有效頻點結果示意圖;
圖14為本發明第一實施例實際數據按3%誤差提取有效頻點結果示意圖。
具體實施方式
下面結合附圖和實施例,對本發明的具體實施方式作進一步詳細描述。以下實施例用于說明本發明,但不用來限制本發明的范圍。
本發明以周期電磁勘探信號為例來說明所述一種有源周期信號中有效信息提取的方法。有源電磁勘探信號一種非常重要的周期信號,在地球物理勘探領域有非常重要的作用。電磁勘探方法是一種基于麥克斯韋電磁傳播理論的重要地球物理勘探方法。無論是針對大地構造、油氣勘探、礦藏勘察,還是針對各種工程勘探,都起到重要的作用,解決了大量的實際問題。
如圖1所示,一種有源周期信號中有效信息提取的方法,包括:
S1,基于原始信號的頻率域頻譜,利用所述原始信號中有效頻率的相鄰頻率的頻譜值對所述有效頻率進行預處理,獲得預處理后的頻譜;
S2,利用離散小波變換將所述預處理后的頻譜分解為高頻成分和低頻成分;
S3,將所述高頻成分解析包絡后的高頻包絡線與所述低頻成分進行重構,獲得整體頻譜曲線的包絡線;
S4,基于整體頻譜曲線的包絡線,進行噪聲評價并提取有效信號。
本發明創新在于通過在周期信號的頻率域上的噪聲評價來估計噪聲的影響上界,而不是傳統上估計噪聲的頻譜值。本發明中噪聲分為周期噪聲和非周期噪聲兩大類,周期噪聲的影響容易分開,本發明著重針對非周期噪聲的影響進行估計。由于非周期噪聲的頻譜是復雜的高振蕩曲線,沒有數學算法可以只在頻率域解出其準確值;本發明并不需要計算出噪聲的準確值,只需要通過估計振蕩函數的上界來估計噪聲的最大影響。如果噪聲的最大影響依然符合信號規范的要求,那么噪聲的實際影響值一定符合規范的要求。
作為一個可選的實施例,所述S1進一步包括:
S1.1,利用混合基快速傅里葉變換獲得所述原始信號的頻率域頻譜;
S1.2,將所述原始信號中有效頻率的頻譜值設置為相鄰頻率的頻譜值的平均值,從而獲得預處理后的頻譜。
圖2為本發明對原始信號數據的頻譜曲線。在本實施例中所述原始信號為仿真信號,所述仿真信號擁有1Hz的主頻,并存在3~199Hz共計99個諧波成分,能量最大值為60,能量依次衰減。如果沒有噪聲干擾時,有效信號的頻率譜為一系列的尖脈沖,但是實際數據總是受到各種干擾影響,在頻率域能量不再只分布在那些有效頻點上,在所有頻率位置都存在能量。
本發明通過估計振蕩函數計算噪聲部分在有效頻率的影響最大值;在進行估計之前,需要優化原始頻譜圖。本實施例的優化處理是:將原始信號頻譜的有效頻率的頻譜值設置為相鄰兩個頻率的譜數值的平均數,其他頻率位置的頻譜值保持不變,從而獲得噪聲的預處理頻譜圖,為接下來的估計算法準備。圖3示為對所述原始信號頻率域頻譜預處理后的頻譜示意圖。如圖3所示,與圖2相比,在有效頻率點位置的脈沖消失了。
作為一個可選的實施例,所述S2進一步包括:
S2.1,對所述預處理后的頻譜進行第一級離散小波變換,分解為第一低頻部分和第一高頻部分;
S2.2,對所述第一低頻部分進行第二級離散小波變換,分解為第二低頻部分和第二高頻部分;
S2.3,對所述第二低頻部分進行第三級離散小波變換,分解為第三低頻部分和第三高頻部分。
作為一個可選的實施例,所述S1中所述高頻成分為所述第一高頻部分、所述第二高頻部分和所述第三高頻部分疊加后的高頻成分;所述低頻成分為所述第三低頻部分。
圖4為本發明對信號對所述原始信號進行三級小波分解的示意圖。本實施例中,首先對信號S進行第一級小波分解得到第一低頻部分A1和第一高頻部分D1;然后對第一低頻部分A1進行第二級小波分解,得到第二低頻部分A2和第二高頻部分D2;再對第二低頻部分A2進行第三級小波分解得到第三低頻部分A3和第三高頻部分D3。
圖5為本發明中應用三級小波分解的高頻部分和低頻部分。如圖5所示頻域信號被分成低頻成分和高頻成分。其中低頻成分為A3,而高頻成分為D1+D2+D3。
作為一個可選的實施例,所述S3進一步包括:
S3.1,利用希爾伯特變換對所述高頻成分進行解析包絡,獲得第一包絡線;
S3.2,選取所述第一包絡線的極大值進行樣條插值,獲得所述高頻包絡線;
S3.2,將所述高頻包絡線與所述低頻成分進行重構,獲得整體頻譜曲線的包絡線。
圖6為本發明中基于希爾伯特變換的解析包絡理論示意圖。本實施例中原始信號為一段窄帶振蕩信號f(s),是一段衰減函數和一段振蕩函數的乘積信號。對f(s)進行希爾伯特變換得到H(f(s)),把H(f(s))作為虛部,f(s)作為實部,構成一個新的信號fA(s),稱作為基于希爾伯特的解析信號,見式(1)
fA(s)=f(s)+iH(f(s)).(1)
fA即為構成的解析信號,|fA|即為對應實數信號的上包絡曲線,其中
圖6中振蕩曲線的上方的連續曲線即為包絡曲線,可以發現原始振蕩曲線在所有位置都小于包絡曲線的數值。需要注意的是,基于希爾伯特變換的解析包絡方法是針對窄帶振蕩曲線的,所以原始頻譜并不符合這樣的條件,不應該直接對原始頻率譜進行包絡,但是對原始小波進行小波分解后,高頻部分可以認為在局部上是符合基于希爾伯特變換的解析包絡要求的。為了獲得更好的包絡結果,本發明在希爾伯特包絡的基礎上再進行了一次極值包絡,即選取第一次包絡曲線的極大值,然后進行樣條插值獲取第二次包絡曲線。
如圖7所示,應用基于希爾伯特變換的解析包絡方法和極值包絡法對圖5中頻率譜的高頻成分進行包絡,振蕩曲線上方連續的曲線即為包絡線,為本發明所述高頻包絡線。
圖8為本發明中對圖2中的仿真信號進行整體包絡結果。根據圖7中得到的高頻曲線振蕩部分的包絡曲線,與圖5中的低頻部分重構得到原始頻譜的包絡曲線。
作為一個可選的實施例,所述S4進一步包括:
S4.1,將所述整體頻譜曲線的包絡線在有效頻率的頻譜值除以所述有效頻率的原始頻譜值,得到噪聲評價系數;
S4.2,基于所述噪聲評價系數,提取所有噪聲評價系數小于要求數值的有效頻率為所述有效信號。
本實施例中,提取整體頻譜曲線的包絡線在有效頻率點的對應的數值,通過估計算法可以估計得到的噪聲在有效頻率位置的最大影響值。
作為一個可選的實施例,所述S4.1進一步包括:
S4.1.1,獲取所述整體頻譜曲線的包絡線在所有有效頻率的頻譜值,以及獲取所有有效頻率的原始頻譜值;
S4.1.2,基于每一個有效頻率,將所述整體頻譜曲線的包絡線在有效頻率的頻譜值除以所述有效頻率的原始頻譜值,得到每一個有效頻率的噪聲評價系數。
具體的,所述有效頻率包括主頻和諧波。
圖9示為本發明第一實施例包絡計算后包絡比例統計結果示意圖。由于采用的是仿真信號,所以噪聲的實際頻譜是已知的,所以可以對包絡后的估計值與真實值進行比較,來判斷包絡比例。
如圖9a所示,為針對仿真信號包絡比例進行了統計,其中100個頻率點中90個頻率點位置的包絡值要大于噪聲的實際能量值。如圖9b所示,10個包絡值小于噪聲能量值的位置,基本上也大于噪聲能量值的70%,說明包絡值和噪聲在有效頻率能量值是在同一尺度,同樣能夠反映噪聲的影響幅度。綜上,包絡曲線在有效頻率的數值能夠作為衡量噪聲最大影響幅度的標準。
圖10為本發明第一實施例噪聲最大影響和實測數據的關系示意圖。如圖10所示的噪聲在有效頻點的最大影響值與實測數據的關系圖,在有效頻率的準確值將會落在虛線框內,而準確值就是需要獲取的有效信號;最大影響值越小,則虛線框的半徑就越小,所獲取的有效信號就越可靠。
圖11為本發明通過包絡后噪聲的估計評價數示意圖。如圖11所示為仿真信號噪聲最大影響值與實測數據頻譜相比得到的噪聲評價數曲線。如果認為小于5%認為是合格的信號,將有93個頻點符合要求,這相比只根據經驗提取幾個有效頻率信號是非常高效的,所以通過本發明中提到的噪聲評價方法可以更有效的提取合格的有效信號。
圖12為本發明第一實施例實際數據的包絡結果示意圖。如圖12所示,針對2n序列偽隨機電磁勘探的實際采集數據應用本發明中的包絡算法計算噪聲的影響,下部鋸齒狀連續曲線為噪聲的頻譜,上部的連續曲線為其包絡曲線,而尖脈沖位置為有效信號位置。
圖13為本發明第一實施例實際數據按5%誤差提取有效頻點結果示意圖。根據圖12中得到的包絡曲線結果,計算所有有效頻點(包括主頻和諧波)位置的噪聲評價數,提取所有噪聲評價數小于5%的結果。其中可以發現過去只提取主頻信號,40Hz以下信號共計28個頻率,而通過應用本發明能夠提取到105個頻率,大大提高了有效信號的數量和效率。
圖14為本發明第一實施例實際數據按3%誤差提取有效頻點結果示意圖。根據圖12中得到的包絡曲線結果,計算所有有效頻點(包括主頻和諧波)位置的噪聲評價數,提取所有噪聲評價數小于3%的結果。只提取主頻信號,40Hz以下信號共計28個頻率,而通過應用本發明能夠提取到44個頻率,大大提高了有效信號的數量和效率。
本發明還提供一種有源周期信號中有效信息提取的裝置,包括:
預處理模塊,用于基于原始信號的頻率域頻譜,利用所述原始信號中有效頻率的相鄰頻率的頻譜值對所述有效頻率進行預處理,獲得預處理后的頻譜;
高低頻分解模塊,用于利用離散小波變換將所述預處理后的頻譜分解為高頻成分和低頻成分;
包絡線模塊,用于將所述高頻成分解析包絡后的高頻包絡線與所述低頻成分進行重構,獲得整體頻譜曲線的包絡線;
有效信號提取模塊,用于基于整體頻譜曲線的包絡線,進行噪聲評價并提取有效信號。
總體而言,本發明涉及一種基于混合基快速傅里葉變換(Mix Radix FFT)、離散小波變換(DWT)及希爾伯特變換(Hilbert Transform)的針對周期信號的噪聲評價方法,并根據受噪聲影響情況提取符合條件的高信噪比信號。所述方法包括:應用混合基快速傅里葉變換獲得原始信號的頻率域頻譜;在頻率域,將有效頻率的頻譜值設為相鄰頻率的頻譜值的平均值,作為預處理后的頻譜;應用離散小波變換將預處理頻譜曲線分成高頻成分(H)和低頻成分(L);對分解得到的高頻成分進行基于希爾伯特變換的解析包絡,同時為了獲得更大的包絡比例,可以對包絡曲線再做一次極值包絡,然后得到的包絡曲線與小波分解的低頻成分重構得到整體頻譜曲線的包絡線;拾取包絡線在有效頻率的數值,除以在有效頻率位置的原始頻譜值,得到噪聲影響程度值,即噪聲評價系數;根據噪聲影響程度值,提取符合信噪比要求的有效信號。
本發明所述噪聲評價及有效信號提取的方法,能夠得到不同頻率信號的信噪比數值,并以此提取符合生產要求的有效信號信息;所述噪聲評價及提取有效信息方法可以應用于所有周期信號,尤其是對周期信號中不容易分解的非周期噪聲的影響評價具有良好的效果,可以大大的提高有效信號提取的數量和效率,具有良好的應用前景。
最后,本申請的方法僅為較佳的實施方案,并非用于限定本發明的保護范圍。凡在本發明的精神和原則之內,所作的任何修改、等同替換、改進等,均應包含在本發明的保護范圍之內。
- 還沒有人留言評論。精彩留言會獲得點贊!