基于數學形態學和IFOA?SVR的滾動軸承可靠度預測方法與流程
本發明涉及一種基于數學形態學和IFOA-SVR的滾動軸承可靠度預測方法,涉及滾動軸承可靠度預測技術領域。
背景技術:
滾動軸承是旋轉機械中的關鍵部件,一旦出現故障將會造成大量的經濟損失甚至危害人的生命安全[1-2]。因此,準確預測滾動軸承在下一階段的工作狀態是合理制定機械設備維修計劃的前提基礎[3-4]。
目前,滾動軸承振動信號的特征提取方法研究受到學者的廣泛關注。文獻[5]提出了基于形態分量分析和包絡譜的滾動軸承故障診斷方法,該方法可有效提取滾動軸承振動信號中的故障特征。文獻[6]提出局部均值分解與形態學分形維數相結合的滾動軸承故障診斷方法,可有效地對滾動軸承進行故障診斷。本發明將Hilbert包絡解調與形態學分形維數結合,對滾動軸承全壽命數據提取出數學形態學分形維數,并將其作為性能退化狀態特征。
在建立支持向量回歸(Support vector regression,SVR)模型方面,文獻[7]利用粒子群算法(Particle swarm optimization,PSO)優化最小二乘SVR對滾動軸承的性能退化趨勢進行了20點預測,平均絕對百分誤差(Mean absolute percentage error,MAPE)為15.82%。文獻[8]利用交叉驗證法對C,g尋優建立SVR模型,對滾動軸承故障趨勢進行了7點預測,MAPE為0.2%。文獻[9]通過經驗選取C,g參數建立SVR模型,并對電廠汽輪發電機組轉子的振動幅值進行了30點預測,平均絕對誤差(Mean absolute error,MAE)為0.6424,MAPE為1.48%。文獻[10]利用PSO對SVR模型中的C,g以及ε尋優,預測航空飛行器的剩余壽命。文獻[7]到文獻[9]預測步長較短,文獻[8]和[9]只對SVR模型中的C和g進行選取,并沒有提出對不敏感誤差ε的取值問題。同時,憑經驗選取C和g有很大的盲目性,通過交叉對比測試確定C和g的值則需要進行大量的實驗,而PSO相對復雜,并且容易陷入局部最優,導致對模型參數的賦值不夠準確。文獻[11]提出一種果蠅優化算法(Fruit fly optimization algorithm,FOA)。文獻[12]提出遞減步長果蠅優化算法(Diminishing step fruit fly optimization algorithm,DS-FOA)實現了全局搜索能力和局部尋優能力的平衡。但DS-FOA在二維空間進行搜索,不能真實反映果蠅的覓食行為。SVR模型內部參數的選取會對SVR的預測精度以及預測步長產生較大影響,本發明采用在三維空間搜索的改進果蠅優化算法(Improved fruit fly optimization algorithm,IFOA)對SVR模型中的3個參數C、g以及ε同時進行參數尋優。并且在進行預測時,將MAE、均方根誤差(Root mean square error,RMSE)、歸一化均方誤差(Normalized mean square error,NMSE)以及MAPE的和作為適應度函數,相比于任一誤差作為適應度函數具有更強的尋優能力。
在可靠度模型方面,可靠度理論已被應用于機械工程以及航空航天等各個領域[13]。比例故障率模型的優勢在于將軸承的性能退化特征與可靠度理論相結合,這樣,軸承的可靠度評估就能夠在設備狀態監測數據的基礎上得到更新。文獻[14]提出將峭度、均方根作為特征指標,利用威布爾比例故障率模型(Weibull proportional hazard model,WPHM)作為可靠度評估模型,并利用fminsearch優化函數求解極大似然方程組確定WPHM的待定參數,有效地對鐵路機車輪對軸承進行可靠度評估。文獻[15]在估計WPHM的待定參數時,利用牛頓迭代法對極大似然方程組進行求解。但上述兩種求解方法都需要根據經驗設定搜索初值,并且運算時間較長。本發明將極大似然方程組中每個方程的絕對值的和作為IFOA的適應度函數,向適應度函數最小的方向優化,可以快速求出方程組的解,確定WPHM的待定參數。
技術實現要素:
本發明為了保證滾動軸承運行狀態可靠度的預測精度同時增加預測步長,提出一種數學形態學分形維數結合改進果蠅優化算法-支持向量回歸(Improved fruit fly optimization algorithm-support vector regression,IFOA-SVR)的滾動軸承可靠度預測方法,即提出一種基于數學形態學和IFOA-SVR的滾動軸承可靠度預測方法。
本發明為解決上述技術問題采取的技術方案是:
一種基于數學形態學和IFOA-SVR的滾動軸承可靠度預測方法,所述方法的實現過程為:
步驟一、求出包絡信號的數學形態學分形維數DM;
步驟二、從獲取的數學形態學分形維數DM選取訓練樣本對,基于所述訓練樣本對利用IFOA對SVR模型中的參數C、g以及ε同時進行尋優,建立IFOA-SVR預測模型:
構建IFOA的過程:
(1)初始化算法參數:設置果蠅種群規模Sizepop,最大覓食代數Maxgen,并隨機初始化果蠅群體位置坐標(X0,Y0,Z0);
(2)果蠅個體利用嗅覺隨機搜索的方向和距離可以通過式(12)獲得
式中,i=1,2,...,Sizepop,L0為初始步長值,gen為當前覓食代數;
(3)由于無法確定食物源的具體位置,所以需要通過式(13)估計第i個果蠅個體的當前位置與坐標原點間的距離Disti,之后計算出味道濃度判定值Si
Si=1/Disti (14)
(4)將Si代入味道濃度判定函數,計算出果蠅個體當前位置的味道濃度
Smelli=function(Si) (15)
(5)當前果蠅群體中具有最高味道濃度的個體,可由式(16)獲得
[bestSmell,bestIndex]=max(Smelli) (16)
式中,bestSmell表示果蠅群體中具有最高味道濃度的個體的味道濃度值,bestIndex表示果蠅群體中具有最高味道濃度的個體的位置;
(6)保留果蠅群體中最佳味道濃度值和與其對應的個體坐標,同時果蠅群體利用自身的視覺對食物源進行定位,然后飛往食物源所在的位置;
(7)進入迭代尋優過程,重復步驟(2)-(5),并判斷當前味最高道濃度是否好于前一迭代味道濃度,且gen<Maxgen;若成立,則執行步驟(6);
建立IFOA-SVR模型,其過程為:
(1)初始化IFOA參數,包括Sizepop、Maxgen以及果蠅個體初始位置;對SVR中的3個參數:懲罰系數C、核函數參數g以及不敏感誤差ε進行尋優,所以初始坐標為(X01,Y01,Z01),(X02,Y02,Z02)和(X03,Y03,Z03);
(2)附與每個果蠅個體隨機方向和飛行距離,并用遞減搜索步長代替固定步長,得到(Xi1,Yi1,Zi1),(Xi2,Yi2,Zi2),(Xi3,Yi3,Zi3),計算當前果蠅個體與原點間距離的倒數,得到味道濃度判定值Si1,Si2和Si3;
(3)確定SVR中參數C、g和ε的范圍,即C∈[2-14,214],g∈[2-14,214],ε∈[2-14,214];
(4)將所述訓練樣本對輸入到SVR模型中,對模型進行訓練,將平均絕對誤差MAE、均方根誤差RMSE、歸一化均方誤差NMSE以及平均絕對百分誤差MAPE的和作為適應度函數,即
(5)找到適應度函數Fitness的最小值對應的果蠅個體,開始迭代尋優,并判斷最小Fitness是否低于前一代最小Fitness;如低于,則保留最小Fitness值及其對應的坐標,并將其賦給初始坐標;如高于,則返回步驟(2);
(6)找到C、g和ε的最佳值,建立IFOA-SVR預測模型;
步驟三、從所述性能退化狀態特征中截取一定長度Z作為WPHM的響應協變量,結合極大似然估計獲得似然函數方程組,把方程組中每個方程絕對值的和作為IFOA的適應度函數,求出方程組的解,確定WPHM的待定參數,進而得到可靠度模型R(t,Z),過程如下:
基于WPHM建立滾動軸承性能退化狀態特征與可靠度之間的數學關系,WPHM的表達式為
式中β為形狀參數,η為尺度參數,μ為協變量回歸參數,t表示時間,Z為截取一定長度的性能退化狀態特征,即從數學形態學分形維數DM中截取一定長度數據;
h(t,Z)和可靠度函數R(t,Z)之間的關系為
從而,R(t,Z)可表示為
利用極大似然估計法得到關于待定參數β、η、μ的方程組并利用IFOA對該方程組進行求解,確定WPHM的表達式h(t,Z)的待定參數β、η、μ的最終取值;將參數β、η、μ代入式(21)即可建立可靠度模型;
步驟四、將性能退化狀態特征的最后一部分數據作為IFOA-SVR預測模型的輸入,采用長期迭代預測法獲取性能退化狀態特征預測結果;
步驟五、將IFOA-SVR預測模型得出的預測結果作為響應協變量嵌入到可靠度模型R(t,Z)中,即可計算出所述性能退化狀態特征預測結果所對應的可靠度,實現滾動軸承可靠度的預測。
在步驟一中,通過Hilbert變換計算出狀態監測數據的包絡信號;
步驟一一、獲取滾動軸承的狀態監測數據:滾動軸承的振動信號;
步驟一二、通過Hilbert變換計算出狀態監測數據的包絡信號;
步驟一三、利用式(4)求出每次采集振動信號的包絡信號的數學形態學分形維數DM,將DM作為滾動軸承性能退化狀態特征;
式中:DM為信號的Minkowski-Bouligand維數即數學形態學分形維數,c為常數,對和log(1/λ)進行最小二乘線性擬合即可得到對信號數學形態學分形維數DM;λ=1,2,…,λmax,λmax為最大分析尺度;
ASe(λ)為定義在分析尺度λ下f(n)關于Se(n)膨脹和腐蝕運算的覆蓋面積,f(n)表示滾動軸承振動信號的包絡信號;Se(n)為結構元素,為一維離散向量;Se(n)的長度及λmax的值通過控制變量法求得。
本發明的有益效果是:
本發明提出的一種基于數學形態學分形維數結合改進果蠅算法-支持向量回歸(Improved fruit fly optimization algorithm-support vector regression,IFOA-SVR)的滾動軸承可靠度預測方法,充分發揮IFOA-SVR預測模型的優勢,對提取的滾動軸承狀態特征數據進行預測。將預測結果嵌入到已建立的可靠度模型中進行滾動軸承可靠度預測,在保證滾動軸承運行狀態可靠度預測精度的同時增加了預測步長。
該方法首先提取振動信號的包絡信號,計算該包絡信號的數學形態學分形維數,將其作為滾動軸承性能退化狀態特征;其次,利用IFOA對SVR中的參數C,g以及ε同時進行尋優,建立IFOA-SVR預測模型。同時,利用極大似然估計結合IFOA建立威布爾比例故障率模型(Weibull proportional hazard model,WPHM),進而得到可靠度模型;最后,將退化狀態特征作為IFOA-SVR預測模型的輸入,采用長期迭代預測法獲取特征預測結果,并將該結果嵌入到可靠度模型中,從而預測出軸承運行狀態的可靠度。實驗結果表明,利用所提方法對滾動軸承可靠度進行預測,能在保證預測精度的前提下增加預測步長。
具體而言,本發明將Hilbert包絡解調與形態學分形維數結合,對滾動軸承全壽命數據提取出數學形態學分形維數,并將其作為性能退化狀態特征。本發明采用在三維空間搜索的改進果蠅優化算法(Improved fruit fly optimization algorithm,IFOA)對SVR模型中的3個參數C、g以及ε同時進行參數尋優。并且在進行預測時,將MAE、均方根誤差(Root mean square error,RMSE)、歸一化均方誤差(Normalized mean square error,NMSE)以及MAPE的和作為適應度函數,相比于任一誤差作為適應度函數具有更強的尋優能力。本發明將極大似然方程組中每個方程的絕對值的和作為IFOA的適應度函數,向適應度函數最小的方向優化,可以快速求出方程組的解,確定WPHM的待定參數。
附圖說明
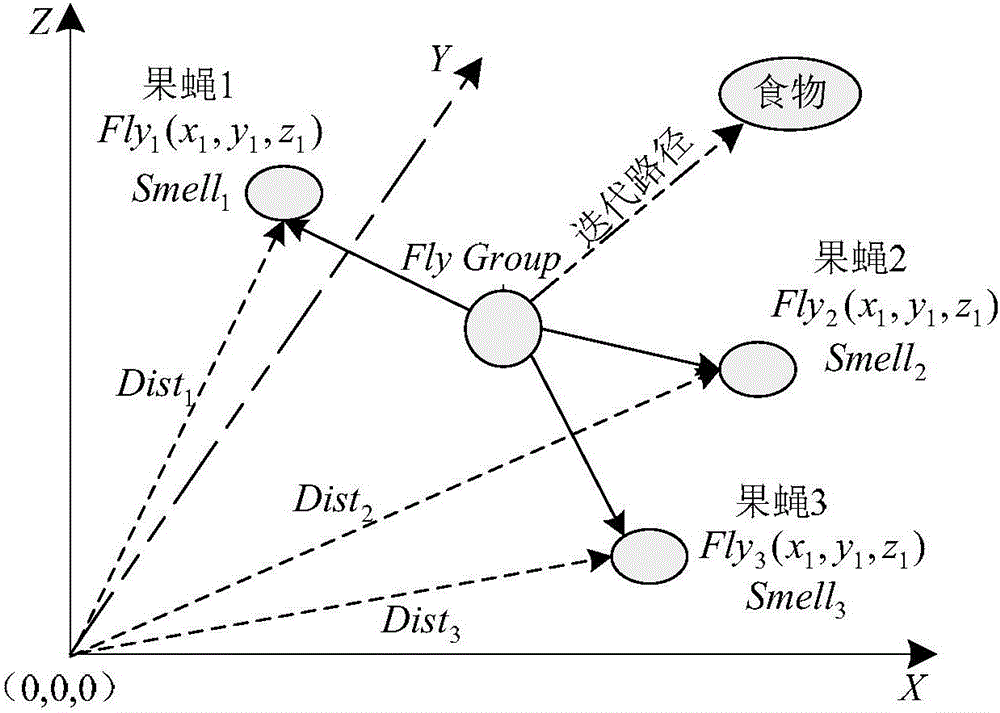
圖1是本發明中的果蠅三維空間覓食示意圖,圖2是本發明的可靠度預測方法流程圖;
圖3為本發明方法在應用中的第860次采集數據的時域波形圖,圖4是本發明方法在應用中對應的第860次采集數據的包絡信號波形圖,圖5為本發明在應用中第1點至第860點的可靠度曲線圖,圖6為本發明在應用中GA優化SVR模型得出的預測結果圖,圖7為本發明在應用中PSO優化SVR模型得出的預測結果圖,圖8為本發明在應用中DS-FOA優化SVR模型得出的預測結果圖,圖9為本發明在應用中IFOA優化SVR模型得出的預測結果圖,圖10為本發明在應用中50點預測數據的可靠度趨勢曲線圖;
圖11為由包絡求分形維數與直接求分形維數的對比圖,本發明采用由由包絡求分形維數。
具體實施方式
具體實施方式一:如圖1至11所示,本實施方式針對所述的基于數學形態學和IFOA-SVR的滾動軸承可靠度預測方法的實現過程具體描述如下:
1基于數學形態學的分形維數
數學形態學包括兩種基本算子,分別是膨脹運算和腐蝕運算。設原始信號f(n)和結構元素Se(n)分別為定義在集合F={0,1,…,N-1}和集合G={0,1,…,M-1}上的兩個一維離散函數,且N≥M。在每一個分析尺度λ下,令Se(n)對f(n)進行一次膨脹和腐蝕運算,即:
式中:表示膨脹運算,Θ表示腐蝕運算,λ=1,2,…,λmax,λmax為最大分析尺度。
定義在尺度λ下f(n)關于Se(n)膨脹和腐蝕運算的覆蓋面積ASe(λ)為
Maragos證明,ASe(λ)滿足式(4)
式中DM為信號的Minkowski-Bouligand維數即數學形態學分形維數,c為常數,對和log(1/λ)進行最小二乘線性擬合即可得到對信號數學形態學分形維數的估計。
2支持向量回歸機
SVR算法一般用于解決數據回歸預測問題,通過建立一個最優超平面,使狀態空間內的各個數據點距離該超平面最近,并將該超平面作為回歸模型進行預測。
訓練樣本對(x1,y1),(x2,y2),…,(xr,yr),xi∈Rn,yi∈R,xi為輸入樣本,yi為輸出樣本,i=1,2,...,r。SVR的回歸函數表達式為
f(x)=<ω·xi>+b (5)
式中<ω·xi>為ω和xi的內積。系數ω和b通過求解式(6)的最小值優化問題獲得
由于擬合曲線必然會存在誤差,但要把誤差控制在一定的可容許范圍內,ε為不敏感誤差,式(6)中Lε為不敏感損失函數,其表達式為
對于回歸錯誤的數據點,需要引入松弛變量ξ和ξ*。將不敏感損失函數Lε代入式(6)可得
滿足約束條件
求解上式時,一般采用對偶理論將其轉化為二次規劃問題。對于非線性數據,引入非線性映射函數Φ,建立拉格朗日方程,通過化簡,可得式(8)的對偶式
式中α,α*為拉格朗日乘子。
令K(xi,xj)=Φ(xi)TΦ(xj)為特征空間的內積,稱K(xi,xj)為核函數,選擇徑向基函數作為核函數。根據KKT定理,可求得變量αi,αi*,b,最終可得支持向量機的回歸函數為
3基于IFOA的SVR尋優
3.1 IFOA算法
FOA是一種基于果蠅覓食行為推演出尋求全局優化的算法。利用在三維空間搜索的IFOA對SVR模型進行優化,可以有效地獲取模型中的最優參數。
如圖1所示為果蠅三維空間覓食示意圖。
IFOA步驟:
(1)初始化算法參數。設置果蠅種群規模Sizepop,最大覓食代數Maxgen,并隨機初始化果蠅群體位置坐標(X0,Y0,Z0)。
(2)果蠅個體利用嗅覺隨機搜索的方向和距離可以通過式(12)獲得
式中,i=1,2,...,Sizepop,L0為初始步長值,gen為當前覓食代數。
(3)由于無法確定食物源的具體位置,所以需要通過式(13)估計第i個果蠅個體的當前位置與坐標原點間的距離Disti,之后計算出味道濃度判定值Si
Si=1/Disti (14)
(4)將Si代入味道濃度判定函數,計算出果蠅個體當前位置的味道濃度
Smelli=function(Si) (15)
(5)當前果蠅群體中具有最高味道濃度的個體,可以由式(16)獲得
[bestSmell,bestIndex]=max(Smelli) (16)
(6)保留果蠅群體中最佳味道濃度值和與其對應的個體坐標,同時果蠅群體利用自身的視覺對食物源進行定位,然后飛往食物源所在的位置。
(7)進入迭代尋優過程,重復步驟(2)-(5),并判斷當前味最高道濃度是否好于前一迭代味道濃度,且gen<Maxgen;若成立,則執行步驟(6)。
3.2 IFOA-SVR模型
(1)初始化IFOA參數。包括Sizepop、Maxgen以及果蠅個體初始位置。由于本發明需要對SVR中的3個參數C、g以及ε進行尋優,所以初始坐標為(X01,Y01,Z01),(X02,Y02,Z02)和(X03,Y03,Z03)。
(2)附與每個果蠅個體隨機方向和飛行距離,并用遞減搜索步長代替固定步長,得到(Xi1,Yi1,Zi1),(Xi2,Yi2,Zi2),(Xi3,Yi3,Zi3)。計算當前果蠅個體與原點間距離的倒數,得到味道濃度判定值Si1,Si2和Si3。
(3)確定SVR中參數C、g和ε的范圍,即C∈[2-14,214],g∈[2-14,214],ε∈[2-14,214]。
(4)將訓練樣本對輸入到SVR模型中,對模型進行訓練,將MAE、RMSE、NMSE以及MAPE的和作為適應度函數,即
(5)找到Fitness的最小值對應的果蠅個體,開始迭代尋優,并判斷最小Fitness是否低于前一代最小Fitness。如低于,則保留最小Fitness值及其對應的坐標,并將其賦給初始坐標。如高于,則返回步驟(2)。
(6)找到C、g和ε的最佳值,建立IFOA-SVR預測模型。
4滾動軸承運行狀態可靠度
WPHM建立了設備運行狀態特征指標與可靠度之間的數學關系,表達式為
式中β為形狀參數,η為尺度參數,μ為協變量回歸參數,Z為振動特征指標數據。
h(t,Z)和可靠度函數R(t,Z)之間的關系為
從而,R(t,Z)可表示為
利用極大似然估計法對待定參數β、η、μ進行估計,確定待定參數最終取值。
5滾動軸承可靠度預測方法及流程
在WPHM參數確定的情況下,建立可靠度模型,將特征預測結果嵌入已建立的可靠度模型中,即可預測未來一段時間內軸承運行的可靠度,具體的預測流程見圖2。
(1)通過Hilbert變換計算出狀態監測數據的包絡信號,利用式(4),求出包絡信號的數學形態學分形維數DM。
(2)選取適當的訓練樣本對,并利用IFOA對SVR模型中的參數C、g以及ε同時進行尋優,建立IFOA-SVR預測模型。
(3)選取一定長度的振動特征指標數據作為WPHM的響應協變量,結合極大似然估計獲得似然函數方程組,把方程組中每個方程絕對值的和作為IFOA的適應度函數,求出方程組的解,確定WPHM的待定參數,進而得到可靠度模型。
(4)將振動特征指標數據作為IFOA-SVR預測模型的輸入,采用長期迭代預測法[16]獲取振動特征預測結果。
(5)將IFOA-SVR預測模型得出的預測結果作為響應協變量嵌入到可靠度模型中,即可計算出這些特征預測結果所對應的可靠度,實現滾動軸承可靠度的預測。
針對本明提出的方法進行具體應用與分析
滾動軸承全壽命數據來自于Cincinnati大學[17],每隔10min進行一次數據采集,共采集984次,每次采樣長度為20480點,采樣頻率為20KHz。圖3為第860次采集數據的時域波形,圖4為其對應的包絡信號波形。
在每次采集的數據中,取中間的4096點進行Hilbert變換,求出包絡信號,進而計算出數學形態學分形維數,并作為一個特征數據點。通過控制變量法實驗對比證明,當λmax=11,Se(n)=(0,0,0,0,0,0,0,0,0,0,0,0)時,利用式(4)求出包絡信號的數學形態學分形維數能夠作為刻畫滾動軸承性能退化過程的特征。
將滾動軸承性能退化狀態特征作為響應協變量,取600點到860點之間的特征指標值,采用極大似然估計,利用IFOA求得WPHM模型的待定參數,如表1所示。
表1 WPHM待定參數的估計結果
將待定參數代入式(19),即可確定當數學形態學分形維數作為響應協變量時的WPHM,進而建立可靠度模型,按照式(22)可以計算出滾動軸承在任意時刻下的可靠度
式中m=1,2,…,984,984表示數據采集總次數;
每個數據點等于10分鐘,數據點與時間存在對應關系。
將第1點至第860點之間對應的特征指標值嵌入可靠度模型即可計算出在這段時間內軸承運行的可靠度,如圖5所示。
由圖5可知,滾動軸承在525點左右出現早期故障,在525點以前軸承對應的可靠度為1。之后可靠度開始逐漸減小,到860點時滾動軸承可靠度已經降到0.25附近,此時軸承處于故障程度比較嚴重的狀態。
利用IFOA對SVR中的參數C,g以及ε進行尋優,L0=30,Sizepop=20,Maxgen=100。訓練數據取第680點到第860點,輸入向量維數為20,建立IFOA-SVR預測模型。表2為利用不同的優化算法對SVR進行尋優得到的參數值。
表2利用不同算法尋優得到的3個參數值
預測數據從第861點開始,共進行了50次迭代運算,通過長期迭代預測法得到最終預測結果。如果只優化SVR模型中的C和g,預測誤差會很大并且預測步長較短。
利用GA對SVR模型中的C、g以及ε同時進行尋優,預測結果如圖6所示。
利用PSO對SVR模型中的C、g以及ε同時進行尋優,預測結果如圖7所示。
利用DS-FOA對SVR模型中的C、g以及ε同時進行尋優,預測結果如圖8所示。
利用IFOA對SVR模型中的C、g以及ε同時進行尋優,并將MAE、RMSE、NMSE以及MAPE的和作為適應度函數,預測結果如圖9所示。
實際退化曲線在890點以后呈上升趨勢,由圖6可以看出,預測曲線在890點以后,明顯偏離實際退化曲線,預測效果不好;由圖7可以看出,預測曲線在890點以后上升趨勢不明顯;由圖8可以看出,預測曲線與實際退化曲線較為接近,但是在893至901點,與實際退化曲線相差較大;對比圖6至圖9可以看出,IFOA優化SVR所得出的預測曲線與實際性能退化曲線更為接近,預測效果更好。
為了定量地評估預測結果,分別計算所預測50個點的MAE、RMSE、NMSE和MAPE,計算結果如表3所示。
表3 50點預測誤差分析
由表3可知,在本發明對SVR中3個參數均優化的情況下,進行50點預測時,與GA、PSO以及DS-FOA優化的SVR預測模型相比,IFOA-SVR模型的4類預測誤差均最小,其4類誤差和也最小。證明IFOA具有更好的空間尋優能力,能夠準確地找到SVR模型中參數的最佳值,體現了IFOA-SVR模型在滾動軸承性能退化趨勢預測方面的優勢。
與文獻[7]到[9]對比分析可知,本發明所得實驗結果MAPE低于文獻[7],預測步長增加了30點;與文獻[8]相比,MAPE在同一數量級內稍高,但預測步長增加了43點;相比于文獻[9],在降低了MAE和MAPE的同時預測步長增加了20點。
將預測所得50點數據嵌入可靠度模型中,可以計算出這50點的可靠度值,可靠度曲線如圖10所示。
從圖10中可以看出,第861點的可靠度值在0.25附近,并且這50點的可靠度呈下降趨勢,到910點時可靠度已經下降到0.08左右。這表明軸承運行狀態很差,已經出現非常嚴重的故障,應該做好及時更換軸承的準備。
通過對本發明方法的應用得出如下結論:
(1)提出Hilbert包絡解調與數學形態學分形維數相結合的特征提取方法。通過控制變量法得出最大分析尺度λmax以及結構元素Se這兩個參數的最佳設置,計算出包絡信號的出數學形態學分形維數并作為刻畫滾動軸承性能退化過程的特征。
(2)將MAE、RMSE、NMSE以及MAPE的和作為IFOA的適應度函數,對SVR模型中的3個參數進行尋優,建立了IFOA-SVR模型。利用該模型對滾動軸承的性能退化趨勢進行了50點預測,與GA,PSO和DS-FOA優化的SVR模型相比預測誤差最小。同時,與相關文獻進行了橫向對比,在保證預測精度的前提下,增加了預測步長。
(3)利用IFOA求解WPHM的待定參數,建立了可靠度模型。將IFOA-SVR模型所得的特征預測結果嵌入到可靠度模型中,得到可靠度預測曲線,能夠預測滾動軸承在未來50點的運行狀態可靠度。
本發明中涉及的參考文獻:
[1]何正嘉,曹宏瑞,訾艷陽,等.機械設備運行可靠性評估的發展與思考[J].機械工程學報,2014,50(2):171-186.
HE Zhengjia,CAO Hongrui,ZI Yanyang,et al.Developments and Thoughts on Operational Reliability Assessment of Mechanical Equipment[J].Journal of Mechanical Engineering,
2014,50(2):171-186.
[2]WANG Zhonglai,HUANG Hongzhong,LI Yanfeng.An approach to reliability assessment under degradation and shock process[J].IEEE Transactions on Reliability,2011,60(4):852-863.
[3]何群,李磊,江國乾,等.基于PCA和多變量極限學習機的軸承剩余壽命預測[J].中國機械工程,2014,25(7):984-988+989.
HE Qun,LI Lei,JIANG Guoqian,et al.Residual Life Predictions for Bearings Based on PCA and MELM[J].China Mechanical Engineering,2014,25(7):984-988+989.
[4]申中杰,陳雪峰,何正嘉,等.基于相對特征和多變量支持向量機的滾動軸承剩余壽命預測[J].機械工程學報,2013,49(2):183-189.
SHEN Zhongjie,CHEN Xuefeng,HE Zhengjia,et al.Remaining Life Predictions of Rolling Bearing Based on Relative Features and Multivariable Support Vector Machine[J].Journal of Mechanical Engineering,2013,49(2):183-189.
[5]陳向民,于德介,李蓉.基于形態分量分析和包絡譜的軸承故障診斷[J].中國機械工程,2014,25(8):1047-1052+1053.
CHEN Xiangmin,YU Dejie,LI Rong.Fault Diagnosis of Rolling Bearings Based on Morphological Componenet Analysis and Envelope Spectrum[J].China Mechanical Engineering,2014,25(8):1047-1052+1053.
[6]張亢,程軍圣,楊宇.基于局部均值分解與形態學分形維數的滾動軸承故障診斷方法[J].振動與沖擊,2013,32(9):90-94.
ZHANG Kang,CHENG Junsheng,YANG Yu.Roller bearing fault diagnosis based on local mean decomposition and morphological fractal dimension[J].Journal of Vibration and Shock,2013,32(9):90-94.
[7]陳昌,湯寶平,呂中亮.基于威布爾分布及最小二乘支持向量機的滾動軸承退化趨勢預測[J].振動與沖擊,2014,33(20):52-56.
CHEN Chang,TANG Baoping,LU Zhongliang.Degradation trend prediction of rolling bearings based on Weibull distribution and least squares support vector machine[J].Journal of Vibration and Shock,2014,33(20):52-56.
[8]宋梅村,蔡琦.基于支持向量回歸的設備故障趨勢預測[J].原子能科學技術,2011,45(8):972-976.
SONG Meicun,CAI Qi.Fault Trend Prediction of Device Based on Support Vector Regression[J].Atomic Energy Science and Technology,2011,45(8):972-976.
[9]朱霄珣.基于支持向量機的旋轉機械故障診斷與預測方法研究[D].北京:華北電力大學,2013.
ZHU Xiaoxun.Research on Rotating Machine Fault Diagnosis and State Prediction Method Based on Support Vector Machine[D].Beijing:North China Electric Power University,2013.
[10]P.J.García Nieto,E.García-Gonzalo,F.Sánchez Lasheras et al.Hybrid PSO-SVM-based method for forecasting of the remaining useful life for aircraft engines and evaluation of its reliability[J].Reliability Engineering and System Safety,2015,138:219-231.
[11]PAN W T.A new fruit fly optimization algorithm:Taking the financial distress model as an example[J].Knowledge-Based Systems,2012,26(2):69-74.
[12]寧劍平,王冰,李洪儒,等.遞減步長果蠅優化算法及應用[J].深圳大學學報理工版,2014,31(4):367-373.
NING Jianping,WANG Bing,LI Hongru,et al.Research on and application of diminishing step fruit fly optimization algorithm[J].Journal of Shenzhen University Science and Engineering,2014,31(4):367-373.
[13]張義民,孫志禮.機械產品的可靠性大綱[J].機械工程學報,2014,50(14):14-20.
ZHANG Yimin,SUN Zhili.The Reliability Syllabus of Mechanical Products[J].Journal of Mechanical Engineering,2014,50(14):14-20.
[14]丁鋒,何正嘉,訾艷陽,等.基于設備狀態振動特征的比例故障率模型可靠性評估[J].機械工程學報,2009,45(12):89-94.
DING Feng,HE Zhengjia,ZI Yanyang,et al.Reliability Assessment Based on Equipment Condition Vibration Feature Using Proportional Hazards Model[J].Journal of Mechanical Engineering,2009,45(12):89-94.
[15]陳昌.基于狀態振動特征的空間滾動軸承可靠性評估方法研究[D].重慶:重慶大學,2014.
CHEN Chang.Reliability Assessment Method for Space Rolling Bearing Based on Condition Vibration Feature[D].Chongqing:Chongqing University,2014.
[16]董紹江.基于優化支持向量機的空間滾動軸承壽命預測方法研究[D].重慶:重慶大學,2012.
DONG Shaojiang.Research on Space Bearing Life Prediction Method Based on Optimized Support Vector Machine[D].Chongqing:Chongqing University,2012.
[17]Rexnord technical services,bearing data set,IMS,University of Cincinnati,NASA Ames Prognostics Data Repository,NASA Ames,Moffett Field,CA,2007[2014-04].http://ti.arc.nasa.gov/project/prognostics-data-repository.
- 還沒有人留言評論。精彩留言會獲得點贊!