一種延性材料單軸本構關系測試方法與流程

本發明涉及材料力學性能測試，具體涉及一種延性材料單軸本構關系測試方法。

背景技術：

延性材料單軸本構關系(即拉伸應力-應變關系)是采用連續介質力學方法進行結構分析并實現工程設計的基礎物理關系，也是聯系材料與力學的重要“紐帶”，對工程構件的設計和安全評價起著關鍵作用；在傳統的拉伸試驗中，試樣等直段的真實橫截面積和標距在拉伸試驗過程中不斷發生變化，在試樣出現頸縮后，頸縮位置的材料不再處于平面變形，標距段工程應力-應變曲線表現出工程應力隨測試應變增長而大幅下降的趨勢；事實上，雖然試樣頸縮后響應載荷會發生下降，但材料在頸縮過程中卻仍在不斷硬化，真實的應力則不斷增大，試樣頸縮區橫截面中心點已處于三軸應力狀態；因此，依靠傳統的等直試樣測量方法無法真實獲得材料頸縮后的應力-應變關系。

技術實現要素：

本發明提供一種簡單的、能夠獲得真實材料頸縮后的應力-應變關系測試方法。

本發明采用的技術方案是：一種延性材料單軸本構關系測試方法，包括以下步驟：

獲取材料試樣的連續載荷P和位移V的關系，所述試樣為長方形中心具有圓孔的板狀結構，P-V曲線滿足下述關系

式中：R試樣圓孔半徑，S為彈性剛度，P*為特征載荷，m為位移指數，V_y為試樣屈服位移；

根據S、P*和m獲取材料的本構關系參數，包括彈性模量E、名義屈服應力σ_y和應變硬化指數n，通過有限元模擬得到臨界斷裂應力σ_f和臨界斷裂應變ε_f，即可確定材料的單軸本構關系；

其中S、P*和m滿足下述關系：

式中：v^*為特征能量密度，A*為特征面積，W為試樣的寬度，T為試樣的厚度，k₁～k₅為無量綱常數；

其中：v^*、A*滿足下述關系：

v^*＝Eⁿσ_y^1-n/(1+n)

A*＝(2W-πR)T

E、σ_y、n滿足下述關系：

式中：σ為真應力，ε為真應變，K為應變硬化系數，且滿足K＝Eⁿσ_y^1-n。

進一步的，所述試樣中心圓孔半徑R和試樣寬度W的比值滿足0.2≤R/W≤0.4。

進一步的，所述連續載荷P和位移V的關系通過試樣的準靜態拉伸試驗獲取。

進一步的，所述S、P*和m由試驗獲取的數據回歸得到。

進一步的，所述參數k₁-k₅通過有限元分析實現標定。

本發明的有益效果是：

(1)本發明相對于傳統的等直試樣，方法簡便易行，所得本構關系范圍更為廣泛；

(2)本發明采用中心具有圓孔的板狀試樣，在拉伸試驗過程中，圓孔邊緣中心點材料單元因三軸度不變而處于單軸應力狀態，相對于等直試樣，可避免頸縮對試驗結果的嚴重影響。

附圖說明

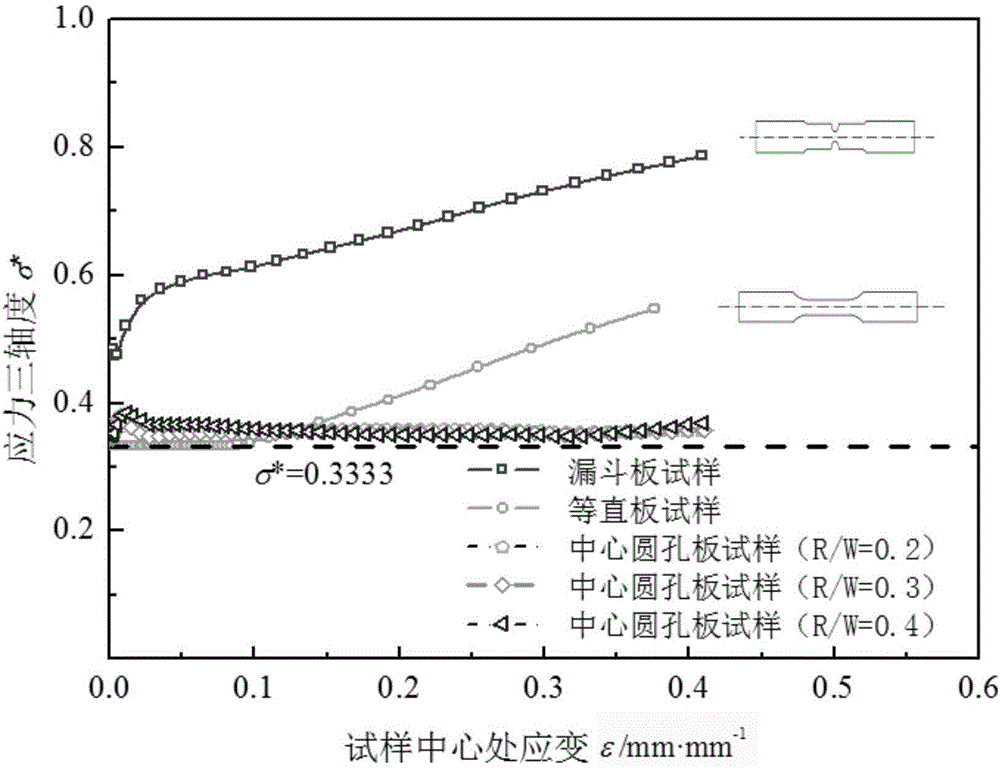
圖1為試樣在拉伸試驗過程中的約束度變化曲線圖。

圖2為鈦合金TA17中心圓孔板試樣拉伸試驗和本發明所得P-V曲線。

圖3為本發明所得鈦合金TA17的大變形單軸本構關系曲線圖。

圖4為本發明中試樣結構示意圖。

具體實施方式

下面結合附圖和具體實施例對本發明做進一步說明。

一種延性材料單軸本構關系測試方法，包括以下步驟：

通過準靜態拉伸試驗，獲取材料試樣的連續載荷P和位移V的關系，所述試樣為中心圓孔板試樣，P-V曲線滿足下述關系：

式中：R試樣圓孔半徑，S為彈性剛度，P*為特征載荷，m為位移指數，V_y為試樣屈服位移；

根據S、P*和m獲取材料的本構關系參數，包括彈性模量E、名義屈服應力σ_y和應變硬化指數n，通過有限元模擬得到臨界斷裂應力σ_f和臨界斷裂應變ε_f，即可確定材料的單軸本構關系；

其中S、P*和m滿足下述關系：

式中：v^*為特征能量密度，A*為特征面積，W為試樣的寬度，T為試樣的厚度，k₁～k₅為無量綱常數；

其中：v^*、A*滿足下述關系：

v^*＝Eⁿσ_y^1-n/(1+n)

A*＝(2W-πR)T

E、σ_y、n滿足下述關系：

式中：：σ為真應力，ε為真應變，K為應變硬化系數，且滿足K＝Eⁿσ_y^1-n，將材料的本構參數代入上式即可得到本材料的本構關系曲線。

試樣中心圓孔半徑R和試樣寬度W的比值滿足0.2≤R/W≤0.4；所述S、P*和m由試驗獲取的數據回歸得到。

本發明采用的技術方案包括兩部分，試樣拉伸試驗和試樣的能量原理模型。

(1)中心圓孔板試樣拉伸試驗

由中心圓孔板試樣拉伸試驗獲取準確的P-V曲線是本發明技術方案的首要條件；中心圓孔板試樣的結構具有特殊性，即在拉伸試驗過程中，圓孔邊緣中心點材料單元因三軸度不變而處于單軸應力狀態，即使在斷裂前出現輕微的頸縮現象，但影響遠小于等直試樣，故采用該試樣進行試驗所得結果可以描述材料單軸應力狀態下的大變形本構關系。

(2)能量原理模型

由理論和有限元分析可知，通過中心圓孔板試樣拉伸試驗所獲取的P-V曲線包含了大量材料信息，通過P-V曲線確定彈性剛度S、特征載荷P*和位移指數m，代入下式：

即可獲取被測材料的本構關系參數：彈性模量E，名義屈服應力σ_y和應變硬化指數n；如圖1所示，中心圓孔板試樣的圓孔邊緣中心點材料單元在頸縮行為發生前處于單軸應力狀態；根據拉伸試驗所得的連續P-V曲線，標定得到彈性剛度S、特征載荷P*以及位移指數m，代入上式即可獲得出材料的本構參數：名義屈服應力σ_y和應變硬化指數n，再通過有限元模擬得到臨界斷裂應力σ_f和臨界斷裂應變ε_f，進而確定材料大變形單軸本構關系。

下面通過具體實施例對本發明進一步說明：

對鈦合金TA17中心圓孔板試樣進行準靜態拉伸試驗并獲取其大變形單軸本構關系曲線，其中試樣寬度W為20mm，厚度T為3mm，中心圓孔半徑R為7.5mm，即R/W＝0.375；試驗設備為美國MTS 810 25KN電液伺服材料試驗機、TestStraⅡ系統、TestWare/SX應用軟件，采用632.12c-21(標距為25mm，軸向測量范圍-10％～50％)應變引伸計測量室溫下試樣標距段的變形；軸向載荷由MTS810試驗機測得。

數據處理過程：首先將試驗所得P-V曲線進行零點修正，然后確定彈性剛度S、特征載荷P*和位移指數m，帶入進行聯立方程求解，即可獲得材料的本構參數E、σ_y和n，再帶入)即可得到材料的本構關系曲線；圖2中將本發明所得P-V曲線與試驗所得P-V曲線進行對比，兩者十分接近；圖3為本發明獲取的鈦合金TA17大變形單軸應力-應變曲線，從圖中可以看出，通過本發明方案獲取的大變形單軸應力-應變關系不僅包含了等直試樣拉伸試驗方法在試樣頸縮以后不能獲取的真實應力、應變，且相對于現有技術方案，本方案所得結果范圍更為廣泛，可行性更高，同時所得結果與現有技術方案具有良好的一致性，即現有技術方案進一步論證了本發明方案的有效性。

在實際應用中，依據情況，本發明使用范圍可作適當修正拓寬；例如，對于不同厚度甚至滿足平面應變條件的中心圓孔板試樣模型，本發明同樣適用，只需將參數k₁-k₅重新通過有限元分析實現標定，然后得到彈性剛度S、特征載荷P*和位移指數m，從而獲取本構關系參數E、σ_y、n，再通過有限元模擬得到臨界斷裂應力σ_f和臨界斷裂應變ε_f，即可確定材料的大變形單軸本構關系。

表1為R/W數值不同時，通過有限元分析標定的參數k₁-k₅；

表1

蔡力勛、姚迪等人針對漏斗圓棒試樣的拉伸試驗通過迭代求解的有限元輔助分析方法，可以獲得延性材料大變形真實應力-應變關系曲線；此方案為圖3中的方案[1]；相對于傳統的等直試樣，其所獲單軸應力-應變關系范圍已大幅度增加；但在約束度的影響下，漏斗圓棒試樣破壞時所得破斷應變遠小于本發明方案所得破斷應變。

本發明適用于等向強化且本構關系符合冪律的延性材料；中心圓孔板試樣的結構具有特殊性，即在拉伸試驗過程中，試樣的圓孔邊緣中心點材料單元在頸縮發生前處于單軸應力狀態，相對于等直試樣，本發明更易于實行，所獲得的單軸應力-應變關系范圍更廣，對工程結構設計和安全評估工作具有重要的意義。

參考文獻

[1]蔡力勛，姚迪，包陳.材料拉伸真實本構曲線測試技術:中國，201210518207[P].2013-6-26.