基于GT?KF?PLS近紅外光譜自適應模型校正方法及系統與流程
本發明屬于近紅外光譜技術在線分析領域,具體涉及一種基于GT-KF-PLS(Gamma test-Kalman filter-Partial least square,伽馬測試的卡爾曼濾波偏最小二乘)近紅外光譜動態演化模型校正方法及系統。
背景技術:
KF-PLS(Kalman FilterPartial Least Squares)已被證明是提高近紅外光譜多元校正模型適應性的一種新方法。采用該方法建立的校正模型具有適應設備陳舊化、環境變化和模型界外樣品等優點。
但是,KF-PLS噪聲方差方法難以得到觀測噪聲不確定的動態近紅外光譜儀測量過程的噪聲方差值,因而常將觀測噪聲方差值置零,并引入了遺忘因子以進行KF-PLS模型校正。這在一定程度上雖然抑制了模型的不確定性發生,但是由于校正模型誤差累積作用,在被測樣品數量不斷增加的情況下,校正模型不可避免地會出現發散現象,甚至完全失效。極大地限制了KF-PLS在觀測噪聲不確定近紅外光譜模型校正中的應用。因此,如何保證自適應校正模型的穩定性成為了難點。
因此,為解決上述問題,本發明提出了一種基于GT-KF-PLS近紅外光譜自適應模型校正方法及系統。
技術實現要素:
為了實現上述目的,本發明提供一種基于GT-KF-PLS(Gamma test-Kalman filter-Partial least square,伽馬測試的卡爾曼濾波偏最小二乘)近紅外光譜自適應模型校正方法及系統,以解決觀測噪聲不確定引起的KF-PLS校正模型發散問題。
本發明提供一種基于GT-KF-PLS近紅外光譜自適應模型校正方法,包括:
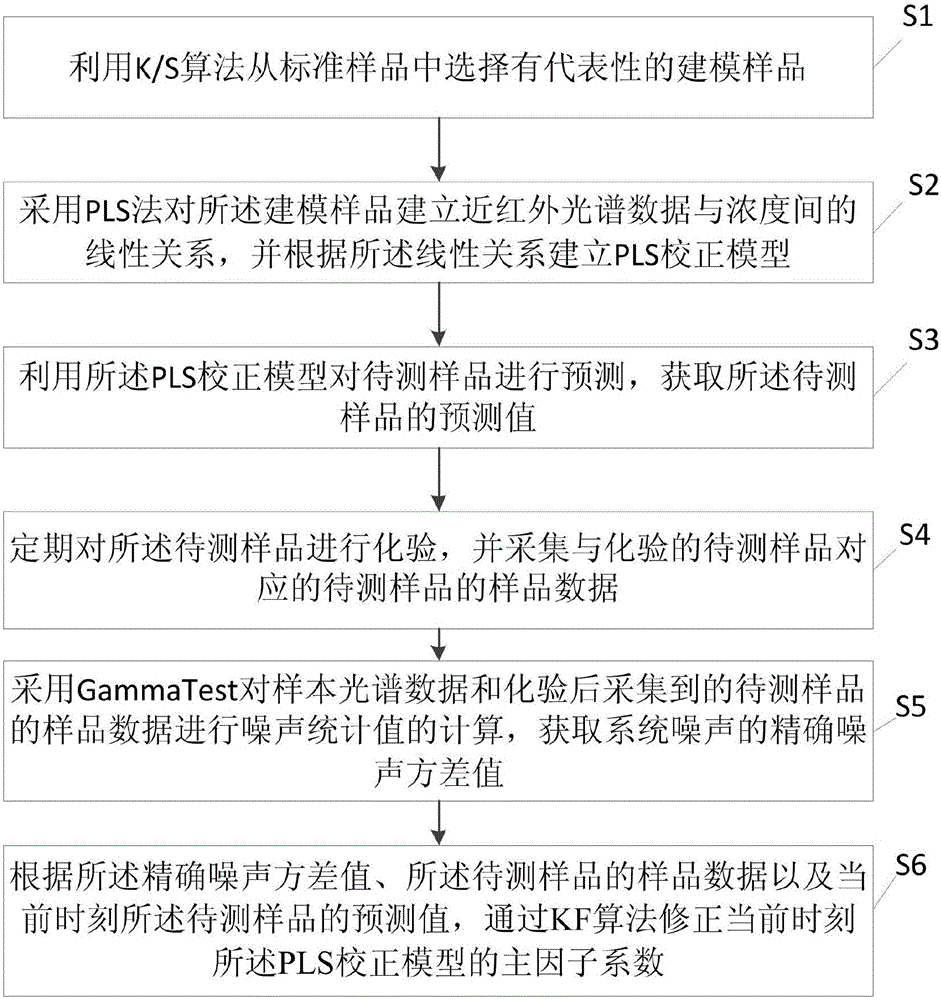
S1:利用K/S算法從標準樣品中選擇有代表性的建模樣品;
S2:采用PLS法對所述建模樣品建立近紅外光譜數據與濃度間的線性關系,并根據所述線性關系建立PLS校正模型;
S3:利用所述PLS校正模型對待測樣品進行預測,獲取所述待測樣品的預測值;
S4:同時,定期對所述待測樣品進行化驗,并采集與化驗的待測樣品對應的待測樣品的樣品數據;
S5:采用Gamma Test對樣本光譜數據和化驗后采集到的待測樣品的樣品數據進行噪聲統計值的計算,獲取系統噪聲的精確噪聲方差值;
S6:根據所述精確噪聲方差值、所述待測樣品的樣品數據以及當前時刻所述待測樣品的預測值,通過KF算法修正當前時刻所述PLS校正模型的主因子系數。
此外,優選的方案是,在步驟S2中,在采用PLS法對所述建模樣品建立近紅外光譜數據與濃度間的線性關系的過程中,
設Xm×n為m個樣品在n個波長上的光譜參數矩陣,Ym×p為m個樣品p種成分含量構成的濃度矩陣,將Xm×n與Ym×p分解為如下形式:
X=TPt+E
Y=UQt+F
其中,矩陣T和矩陣U分別表示去掉大部分噪聲后的光譜信息和濃度信息;E和F表示誤差;
由于Xm×n與Ym×p存在線性關系Y=P'X,在分解時,矩陣T和U之間的線性關系為:U=TB;通過交換迭代矢量而使兩個分解過程合二為一。
此外,優選的方案是,在步驟S5中,在采用Gamma Test對樣本光譜數據和化驗后采集到的待測樣品的樣品數據進行噪聲統計值的計算,獲取系統噪聲的精確噪聲方差值的過程中,獲取第i個樣本點對應的系統噪聲方差值包括:
S51:假定數據之間的關系:Y=h(X)+r,
其中,h(X)表示光滑函數;r表示噪聲變量;
S52:使用kd-tree算法在輸入空間對各輸入樣本點Xi(1≤i≤M)進行計算,得到輸入樣本Xi(1≤i≤M)的第K(1≤K≤P)近鄰域點XN[i,K](1≤i≤M),
S53:計算所有Xi(1≤i≤M)的第P近鄰域點的最小均方距離δ(K)以及輸出空間相應的最小均方距離γ(K),
S54:對(δ(K),γ(K))K(1≤K≤P)、(δ(K),γ(K))K(1≤K≤P),按公式γ=Aδ+R進行一次線性回歸,所得一次線性函數的截距,即系統噪聲方差值R;
S55:當新增加一個標準樣品時,重復步驟S51至步驟S54,,得到每個樣品對應噪聲方差。
此外,優選的方案是,在步驟S6中,根據所述精確噪聲方差值、所述待測樣品的樣品數據以及當前時刻所述待測樣品的預測值,通過KF算法修正當前時刻所述PLS校正模型的主因子系數過程中,
設PLS初始模型主因子數為l,主因子系數為:
w1,t1,v1,p1;w2,t2,v2,p2;……;wi,ti,vi,pi(i=1,2,3…,l);
其中:
vi=(tTy)/(tTt)=[vi1 vi2 ... vip]
將所述PLS初始模型中的所有系數值組成狀態向量:
W=[w1Tt1Tv1p1T...wiTtiTvipiT]T(i=1,2,3…,l)
系統的狀態方程和觀測方程表示為:
其中,Yek為標樣濃度;Wk為第k個標樣修正時刻的主因子系數;Xk為第k個樣品光譜矢量;Yrk為預測濃度;
Vk為觀測噪聲,其統計特性為:
令
則觀測方程為:Yek=HkWk+Dk+Vk;
其中,H表示狀態變量Wk對測量變量Yk的增益;
Wk表示k時刻狀態變量,即:用第k個標樣修正時的PLS主因子系數;
Dk為中間變量。
本發明還提供一種基于GT-KF-PLS近紅外光譜自適應模型校正系統,包括:建模樣品選取單元,用于利用K/S算法從標準樣品中選擇有代表性的建模樣品;
PLS校正模型建立單元,用于采用PLS法對所述建模樣品建立近紅外光譜數據與濃度間的線性關系,并根據所述線性關系建立PLS校正模型;
預測值獲取單元,用于利用所述PLS校正模型對待測樣品進行預測,獲取所述待測樣品的預測值;
樣品數據獲取單元,用于定期對所述待測樣品進行化驗,并采集與化驗的待測樣品對應的待測樣品的樣品數據;
精確噪聲方差值獲取單元,用于采用Gamma Test對樣本光譜數據和化驗后采集到的待測樣品的樣品數據進行噪聲統計值的計算,獲取系統噪聲的精確噪聲方差值;
PLS校正模型的主因子系數修正單元,用于根據所述精確噪聲方差值、所述待測樣品的樣品數據以及當前時刻所述待測樣品的預測值,通過KF算法修正當前時刻所述PLS校正模型的主因子系數。
此外,優選的方案是,所述PLS校正模型建立單元在采用PLS法對所述建模樣品建立近紅外光譜數據與濃度間的線性關系的過程中,
設Xm×n為m個樣品在n個波長上的光譜參數矩陣,Ym×p為m個樣品p種成分含量構成的濃度矩陣,將Xm×n與Ym×p分解為如下形式:
X=TPt+E
Y=UQt+F
其中,矩陣T和矩陣U分別表示去掉大部分噪聲后的光譜信息和濃度信息;E和F表示誤差;
由于Xm×n與Ym×p存在線性關系Y=P'X,在分解時,矩陣T和U之間的線性關系為U=TB;通過交換迭代矢量而使兩個分解過程合二為一。
此外,優選的方案是,所述精確噪聲方差值獲取單元在采用Gamma Test對樣本光譜數據和化驗后采集到的待測樣品的樣品數據進行噪聲統計值的計算,獲取系統噪聲的精確噪聲方差值的過程中,獲取第i個樣本點對應的系統噪聲方差值包括:
S51:假定數據之間的關系:Y=h(X)+r,
其中,h(X)表示光滑函數;r表示噪聲變量;
S52:使用kd-tree算法在輸入空間對各輸入樣本點Xi(1≤i≤M)進行計算,得到輸入樣本Xi(1≤i≤M)的第K(1≤K≤P)近鄰域點XN[i,K](1≤i≤M),
S53:計算所有Xi(1≤i≤M)的第P近鄰域點的最小均方距離δ(K)以及輸出空間相應的最小均方距離γ(K),
S54:對(δ(K),γ(K))K(1≤K≤P)、(δ(K),γ(K))K(1≤K≤P),按公式γ=Aδ+R進行一次線性回歸,所得一次線性函數的截距,即系統噪聲方差值R;
S55:當新增加一個標準樣品時,重復步驟S51至步驟S54,,得到每個樣品對應噪聲方差。
此外,優選的方案是,所述PLS校正模型的主因子系數修正單元根據所述精確噪聲方差值、所述待測樣品的樣品數據以及當前時刻所述待測樣品的預測值,通過KF算法修正當前時刻所述PLS校正模型的主因子系數過程中,
設PLS初始模型主因子數為l,主因子系數為:
w1,t1,v1,p1;w2,t2,v2,p2;……;wi,ti,vi,pi(i=1,2,3…,l);
其中:
vi=(tTy)/(tTt)=[vi1 vi2 ... vip]
將所述PLS初始模型中的所有系數值組成狀態向量:
W=[w1Tt1Tv1p1T...wiTtiTvipiT]T(i=1,2,3…,l)
系統的狀態方程和觀測方程表示為:
其中,Yek為標樣濃度;Wk為第k個標樣修正時刻的主因子系數;Xk為第k個樣品光譜矢量;Yrk為預測濃度;
Vk為觀測噪聲,其統計特性為:
令
則觀測方程為:Yek=HkWk+Dk+Vk;
其中,H表示狀態變量Wk對測量變量Yk的增益;
Wk表示k時刻狀態變量,即:用第k個標樣修正時的PLS主因子系數;
Dk為中間變量。
從上面的技術方案可知,本發明提供的基于GT-KF-PLS近紅外光譜自適應模型校正方法及系統,有效利用觀測輸入(樣本近紅外光譜)輸出數據(樣本化驗值),提出樣本有效噪聲方差(Gamma test,GT)改進的KF-PLS模型校正方法;采用衰減記憶的GT對輸入輸出數據進行實時方差估計,得到準確的觀測噪聲方差值,再利用KF-PLS實現精確模型校正,能夠保證近紅外光譜自適應校正模型的穩定性,最終實現基于近紅外光譜技術的在線分析。
附圖說明
通過參考以下結合附圖的說明及權利要求書的內容,并且隨著對本發明的更全面理解,本發明的其它目的及結果將更加明白及易于理解。在附圖中:
圖1為根據本發明實施例的基于GT-KF-PLS近紅外光譜自適應模型校正方法流程示意圖;
圖2為根據本發明實施例的基于GT-KF-PLS近紅外光譜自適應模型校正系統結構框圖。
具體實施方式
在下面的描述中,出于說明的目的,為了提供對一個或多個實施例的全面理解,闡述了許多具體細節。然而,很明顯,也可以在沒有這些具體細節的情況下實現這些實施例。
以下將結合附圖對本發明的具體實施例進行詳細描述。
為了說明本發明提供的基于GT-KF-PLS近紅外光譜自適應模型校正方法,圖1示出了根據本發明實施例的基于GT-KF-PLS近紅外光譜自適應模型校正方法流程。
如圖1所示,本發明提供的基于GT-KF-PLS近紅外光譜自適應模型校正方法包括:
S1:利用K/S算法從標準樣品中選擇有代表性的建模樣品;
S2:采用PLS法對所述建模樣品建立近紅外光譜數據與濃度間的線性關系,并根據所述線性關系建立PLS校正模型;
S3:利用所述PLS校正模型對待測樣品進行預測,獲取所述待測樣品的預測值;
S4:同時,定期對所述待測樣品進行化驗,并采集與化驗的待測樣品對應的待測樣品的樣品數據;
S5:采用Gamma Test對樣本光譜數據和化驗后采集到的待測樣品的樣品數據進行噪聲統計值的計算,獲取系統噪聲的精確噪聲方差值;
S6:根據所述精確噪聲方差值、所述待測樣品的樣品數據以及當前時刻所述待測樣品的預測值,通過KF算法修正當前時刻所述PLS校正模型的主因子系數。
在進行步驟S1之前,首先對原始光譜數據進行矢量歸一化預處理。
在步驟S1中,采用K/S(Kennard-Stone)算法從標準樣品中選擇有代表性的校正集樣品,并按留一交叉驗證的方法確定最終的主因子數。
在步驟S2中,采用PLS法建立近紅外光譜數據與濃度間的線性關系。
設Xm×n為m個樣品在n個波長上的光譜參數矩陣,Ym×p為m個樣品p種成分含量構成的濃度矩陣,PLS法不直接建立每種成份與光譜參數向量的關系方程,而是考慮Xm×n與Ym×p的外部關系和聯系二者的內部關系,將Xm×n與Ym×p分解為如下形式:
X=TPt+E
Y=UQt+F
矩陣T和矩陣U分別表示去掉大部分噪聲后的光譜信息和濃度信息;E和F表示誤差;
由于Xm×n與Ym×p存在線性關系Y=P'X,在分解時,還考慮矩陣T和U之間的線性關系為:U=TB;通過交換迭代矢量而使兩個分解過程合二為一。
在步驟S5中,采用Gamma Test對已知樣本光譜和樣本化驗值數據進行噪聲統計值的計算,得到系統噪聲的精確信息,其中第i個樣本點對應的系統噪聲方差計算過程如下:
S51:假定樣品光譜與標準濃度之間的關系如下Y=h(X)+r,式中h(X)表示光滑函數;r表示噪聲變量。
S52:首先使用kd-tree算法在輸入空間對各輸入樣本點Xi(1≤i≤M)進行計算,得到輸入樣本Xi(1≤i≤M)的第K(1≤K≤P)近鄰域點XN[i,K](1≤i≤M),
S53:計算所有Xi(1≤i≤M)的第P近鄰域點的最小均方距離δ(K)以及輸出空間相應的最小均方距離γ(K),
S54:最后,對(δ(K),γ(K))K(1≤K≤P)、(δ(K),γ(K))K(1≤K≤P),按公式γ=Aδ+R進行一次線性回歸,所得一次線性函數的截距,即為gamma統計值,也即系統噪聲方差值R;
S55:當新增加一個標準樣品時,重復S51至S54的操作。可得到每個樣品對應噪聲方差。
在步驟S6中,基于KF-PLS近紅外光譜與化驗值的模型校正。
需要說明的是,KF因其有很好的自適應動態實時濾波能力,對PLS校正模型進行調整建模,可以有效地對動態系統模型進行子空間演化逼近,獲得動態演化校正模型。利用KF對PLS主因子系數進行估計,將PLS模型主因子系數看作系統狀態變量,標準樣品待測化學值看作系統觀測變量,這樣就把問題轉化為狀態參數的估計問題;即可獲得隨環境噪聲、設備老化和測量對象變化的動態演化校正模型,這種子空間逼近模型可準確反映系統的動態時變特性。
設PLS初始模型主因子數為l,主因子系數為:
w1,t1,v1,p1;w2,t2,v2,p2;……;wi,ti,vi,pi(i=1,2,3…,l);
其中:
vi=(tTy)/(tTt)=[vi1 vi2 ... vip]
為使上述問題中主因子系數的計算轉化為濾波遞推估計形式,將模型中的所有系數值組成狀態向量:
W=[w1Tt1Tv1p1T...wiTtiTvipiT]T(i=1,2,3…,l)
系統的狀態方程和觀測方程表示為:
其中,Yek為標樣濃度,Wk為第k個標樣修正時刻的主因子系數,Xk為第k個樣品光譜矢量,Yrk為預測濃度。Vk為觀測噪聲,其統計特性為:
令
則觀測方程為:Yek=HkWk+Dk+Vk。
其中,H表示狀態變量Wk對測量變量Yk的增益。
Wk:表示k時刻狀態變量,在這里也即是用第k個標樣修正時的PLS主因子系數。Dk沒有特別的含義,只是個中間變量而已。這里是令所以則
在系統的精確噪聲方差值的基礎上,可以采用基于KF-PLS進行精確建模。在儀器使用過程中,新增一個標樣,修正一次模型,并引入遺忘因子,逐漸遺忘陳舊樣品的作用,使校正模型具有適應設備陳舊化、環境變化和模型界外樣品的自適應性。
與上述方法相對應,本發明還提供一種基于GT-KF-PLS近紅外光譜自適應模型校正系統,圖2示出了根據本發明實施例的基于GT-KF-PLS近紅外光譜自適應模型校正系統邏輯結構。
如圖2所示,本發明提供的基于GT-KF-PLS近紅外光譜自適應模型校正系統200,包括:建模樣品選取單元210、PLS校正模型建立單元220、預測值獲取單元230、樣品數據獲取單元240、精確噪聲方差值獲取單元250和PLS校正模型的主因子系數修正單元260。
具體地,建模樣品選取單元210,用于利用K/S算法從標準樣品中選擇有代表性的建模樣品;
PLS校正模型建立單元220,用于采用PLS法對所述建模樣品建立近紅外光譜數據與濃度間的線性關系,并根據所述線性關系建立PLS校正模型;
預測值獲取單元230,用于利用所述PLS校正模型對待測樣品進行預測,獲取所述待測樣品的預測值;
樣品數據獲取單元240,用于定期對所述待測樣品進行化驗,并采集與化驗的待測樣品對應的待測樣品的樣品數據;
精確噪聲方差值獲取單元250,用于采用Gamma Test對樣本光譜數據和化驗后采集到的待測樣品的樣品數據進行噪聲統計值的計算,獲取系統噪聲的精確噪聲方差值;
PLS校正模型的主因子系數修正單元260,用于根據所述精確噪聲方差值、所述待測樣品的樣品數據以及當前時刻所述待測樣品的預測值,通過KF算法修正當前時刻所述PLS校正模型的主因子系數。
其中,PLS校正模型建立單元220在采用PLS法對所述建模樣品建立近紅外光譜數據與濃度間的線性關系的過程中,
設Xm×n為m個樣品在n個波長上的光譜參數矩陣,Ym×p為m個樣品p種成分含量構成的濃度矩陣,將Xm×n與Ym×p分解為如下形式:
X=TPt+E
Y=UQt+F
其中,矩陣T和矩陣U分別表示去掉大部分噪聲后的光譜信息和濃度信息;E和F表示誤差;
由于Xm×n與Ym×p存在線性關系Y=P'X,在分解時,矩陣T和U之間的線性關系為:U=TB;通過交換迭代矢量而使兩個分解過程合二為一。
其中,所述精確噪聲方差值獲取單元250,在采用Gamma Test對樣本光譜數據和化驗后采集到的待測樣品的樣品數據進行噪聲統計值的計算,獲取系統噪聲的精確噪聲方差值的過程中,
獲取第i個樣本點對應的系統噪聲方差值包括:
S51:假定數據之間的關系:Y=h(X)+r,
其中,h(X)表示光滑函數;r表示噪聲變量;
S52:使用kd-tree算法在輸入空間對各輸入樣本點Xi(1≤i≤M)進行計算,得到輸入樣本Xi(1≤i≤M)的第K(1≤K≤P)近鄰域點XN[i,K](1≤i≤M),
S53:計算所有Xi(1≤i≤M)的第P近鄰域點的最小均方距離δ(K)以及輸出空間相應的最小均方距離γ(K),,對(δ(K),γ(K))K(1≤K≤P)
S54:對(δ(K),γ(K))K(1≤K≤P),按公式γ=Aδ+R進行一次線性回歸,所得一次線性函數的截距,即系統噪聲方差值R;
S55:當新增加一個標準樣品時,重復步驟S51至步驟S54,,得到每個樣品對應噪聲方差。
其中,所述PLS校正模型的主因子系數修正單元260根據所述精確噪聲方差值、所述待測樣品的樣品數據以及當前時刻所述待測樣品的預測值,通過KF算法修正當前時刻所述PLS校正模型的主因子系數過程中,
設PLS初始模型主因子數為l,主因子系數為:
w1,t1,v1,p1;w2,t2,v2,p2;……;wi,ti,vi,pi(i=1,2,3…,l);
其中:
vi=(tTy)/(tTt)=[vi1 vi2 ... vip]
將所述PLS初始模型中的所有系數值組成狀態向量:
W=[w1Tt1Tv1p1T...wiTtiTvipiT]T(i=1,2,3…,l)
系統的狀態方程和觀測方程表示為:
其中,Yek為標樣濃度,Wk為第k個標樣修正時刻的主因子系數,Xk為第k個樣品光譜矢量,Yrk為預測濃度。Vk為觀測噪聲,其統計特性為:
令
則觀測方程為:Yek=HkWk+Dk+Vk。
其中,H表示狀態變量Wk對測量變量Yk的增益。
Wk表示k時刻狀態變量,在這里也即是用第k個標樣修正時的PLS主因子系數。Dk沒有特別的含義,只是個中間變量而已。這里是令所以則
通過上述實施方式可以看出,本發明提供的基于GT-KF-PLS近紅外光譜自適應模型校正方法及系統,有效利用觀測輸入(樣本近紅外光譜)輸出數據(樣本化驗值),提出樣本有效噪聲方差(Gamma test,GT)改進的KF-PLS模型校正方法;采用衰減記憶的GT對輸入輸出數據進行實時方差,得到準確的觀測噪聲方差值,再利用KF-PLS實現精確校正模型,能夠保證近紅外光譜自適應校正模型的穩定性,最終實現基于近紅外光譜技術的在線分析。
如上參照附圖以示例的方式描述了根據本發明提出的基于GT-KF-PLS近紅外光譜自適應模型校正方法及系統。但是,本領域技術人員應當理解,對于上述本發明所提出的基于GT-KF-PLS近紅外光譜自適應模型校正方法及系統,還可以在不脫離本發明內容的基礎上做出各種改進。因此,本發明的保護范圍應當由所附的權利要求書的內容確定。
- 還沒有人留言評論。精彩留言會獲得點贊!