基于多通道連續波多普勒雷達的物體運動模式識別方法與流程

本發明涉及非接觸式對物體運動模式識別的方法，尤其是涉及一種基于多通道連續波多普勒雷達的物體運動模式識別方法。

背景技術：

使用連續波多普勒雷達或雷達傳感器技術進行運動檢測近年來取得了很大的進展。連續波雷達傳感器采用單一頻率工作，具有結構簡單、成本低、可集成性好、抗干擾能力強等突出優點。此前其所用的基帶解調算法一般采用小角近似原理或反正切運算，無法實現低采樣率場景下的大動態范圍運動的測量。另外，此前的連續波多普勒雷達或雷達傳感器多用于測量一維運動，并且很少用于運動模式識別方面的應用。

技術實現要素：

為了解決背景技術中存在的問題，本發明的目的在于提供一種基于多通道連續波多普勒雷達的物體運動模式識別方法。上述方法針對解調得到的基帶信號，因此適用于所有采用零中頻、副載波調制、低中頻、超外差或數字中頻架構的雷達或雷達傳感器。

本發明采用的技術方案是：

本發明通過一個天線發射電磁波，照射待測運動物體表面，被反射的信號經2-3個接收天線接收并下變頻到基帶，再應用反正弦算法，即Arcsine算法，分別解調出不受相位模糊度限制的相位信息，得到每個接收天線與待測物體間的距離變化信息，再通過提出的追蹤公式得到物體的運動軌跡，在運動軌跡的基礎上進行模式識別。

所述Arcsine算法是：

對于每個接收天線的任意正交下變頻接收機，其輸出的正交I、Q信號經采樣后，待測物體不受相位模糊度限制的運動相位信息Φ[n]表示為：

式中n表示對I、Q信號的采樣點數，當采樣率足夠高時，即采樣率大于20v/λ，其中v為待測物體的最大運動速度，λ為發射電磁波的波長，上式可以近似等于下式：

Arcsine算法避免了反正切類函數的相位模糊問題，同時在高采樣率即采樣率大于20v/λ和低采樣率即采樣率小于20v/λ但大于4v/λ的條件下保持準確。

當待測物體運動在三維空間中時，使用所述的1個發射天線和3個接收天線，使用如下追蹤公式對待測物體在三維空間中的運動軌跡進行記錄

其中(x_T,y_T,z_T)為發射天線坐標，(x(t),y(t),z(t))為目標物體的實時坐標，(x₁,y₁,z₁)、(x₂,y₂,z₂)、(x₃,y₃,z₃)分別為3個接收天線的坐標，d₁、d₂、d₃分別是電磁波從發射天線發射經待測物體反射后再到各個接收天線走過的距離。

當待測物體運動在二維平面上時，使用所述的1個發射天線和2個接收天線對待測物體的運動軌跡進行記錄；以物體運動平面作為xoy平面，將1個發射天線放置于坐標(0,0,z_T)，2個接收天線分別放置于坐標(x₁,0,z_T)、(x₂,0,z_T)，則上面公式簡化為：

其另一表達方式為：

本發明具有的有益效果是：

本發明的反正弦(Arcsine)算法避免了反正切類函數的相位模糊問題，同時適用于高采樣率和低采樣率的工作條件，并在低采樣率的條件下保持準確。綜合來說，本發明實現了在對待測物體定位和跟蹤的基礎上進行模式識別。具有識別準確率高，抗干擾能力強，架構簡單、成本低的優點，解調出來的運動大多為線性關系，無需復雜數據處理過程，節省硬件資源。

附圖說明

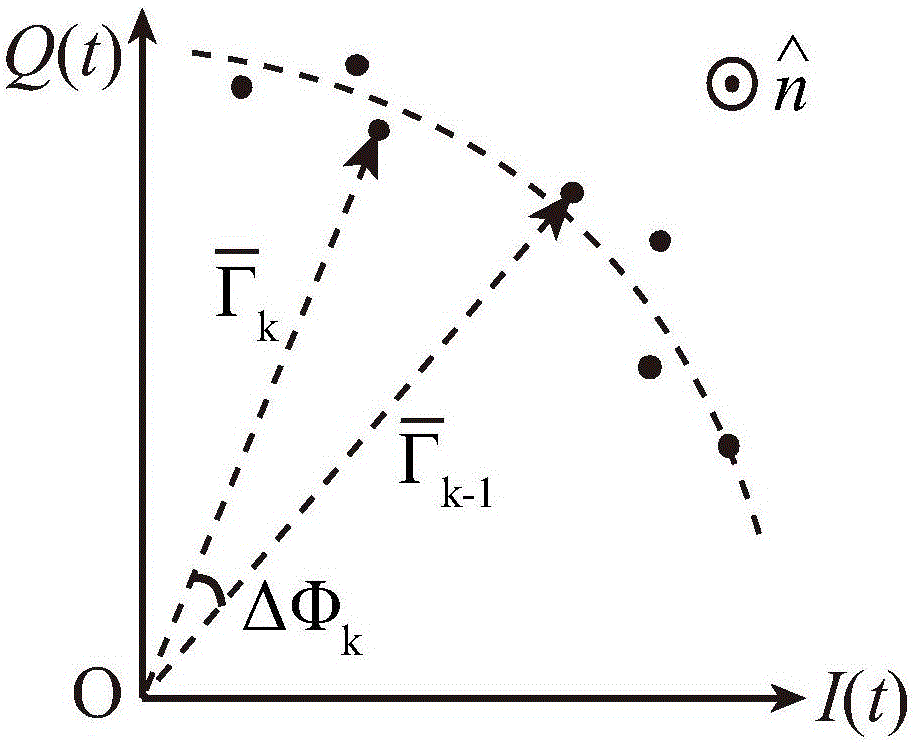
圖1是本發明Arcsine算法的圖解。

圖2是1個發射天線和3個接收天線追蹤物體運動軌跡的立體圖。

圖3是實施例Arcsine算法和直接反正切算法以及反正切加相位解模糊算法的對比結果。

圖4是實施例使用Arcsine解調待測物體單擊和移動兩種運動模式下的距離變化信息的實驗結果。

圖5是實施例在軌跡追蹤基礎上識別待測物體單擊和移動兩種運動模式的實驗結果。

具體實施方式

下面結合附圖和實施例對本發明做進一步的說明。

本發明的工作原理和實施方式：

射頻前端通過1個發射天線發射電磁波，照射待測運動物體表面，反射的信號經兩個接收天線接收并下變頻到基帶。對于任意正交下變頻接收機，其輸出的正交I、Q信號經采樣后，待測物體的距離變化信息x(t)可以表示為：

其中DC_I(t)和DC_Q(t)是直流偏移，A_I(t)和A_Q(t)是I、Q信號的幅度(正交解調時可認為兩者相等)，λ、θ₀分別表示電磁波的波長、收發機的殘余相位噪聲(在相關解調中可認為等于0)和收發信號的額外相差。所以x(t)可由下式得到

由于反三角函數具有(-π/2,π/2)的值域限制，得到的x(t)會包含不連續點，極大地影響測量精度和范圍。為提高系統的魯棒性，將接收到的I、Q信號在去掉直流偏移后，在I-Q星座圖上表示，如圖1所示，記向量和分別表示第k次和第k-1次I、Q信號采樣結果。所以兩個向量夾角可以寫為下式，其中是兩個向量所構成平面的法向量。

對ΔΦ_k累積求和，得：

上式即為無相位模糊度的解調結果，其中n表示對I、Q信號的采樣點數。當和足夠接近，即采樣率足夠高時，上式可以近似等于下式：

通過反正弦(Arcsine)算法得到的相位信息再乘以系數得到物體的運動引起的d₁、d₂的變化量，結合初始時刻d₁、d₂的值d₀₁、d₀₂，即可得到每個時刻d₁、d₂的值。測量d₀₁、d₀₂的技術方案為：發射雙頻副載波到待測物體，接收機分別對兩個頻率的信號進行解調。以d₀₁為例，雙頻副載波兩個頻率的信號經過反正弦(Arcsine)算法解調后各自的相位分別為Φ₁、Φ₂，并滿足以下關系：

當將上面兩式的相位之差控制在一個模糊度范圍內時，即k₁＝k₂，將上兩式相減得到：

對于空間中任意放置的1個發射天線和3個接收天線，如圖2所示，使用如下公式(或其擴展、化簡或等效的公式)對目標在三維空間中的運動模式進行記錄。

其中(x_T,y_T,z_T)為發射天線坐標，(x(t),y(t),z(t))為目標物體的實時坐標，(x₁,y₁,z₁)、(x₂,y₂,z₂)、(x₃,y₃,z₃)分別為3個接收天線的坐標，d₁、d₂、d₃分別是電磁波從發射天線發射經目標反射后再到各個接收天線走過的距離。

當待測物體運動在二維平面上時，使用1個發射天線和2個接收天線對物體的運動模式進行記錄和進行運動模式識別。以物體運動平面作為xoy平面，將1個發射天線和2個接收天線放置在一個平行于xoy平面的直線上，例如發射天線坐標為(0,0,z_T)，2個接收天線坐標分別為(x₁,0,z_T)、(x₂,0,z_T)，則上面的公式簡化為：

其另一表達方式為：

得到軌跡后將其與已構建的模型進行特征匹配來進行識別。特征匹配方法有直接匹配法、動態時間規整法、隱性馬爾科夫模型(HHM)法、神經網絡模型法等。本發明實施例選用的是基于概率統計的隱性馬爾科夫模型(HHM)法，它尤其適用時間序列的建模，對復雜度高的動作也具有很高的識別精度，易于添加或修改手勢庫。使用此種方法首先根據運動軌跡進行模式分類，然后開始訓練，為每一種模式建立一個HHM模型，識別時取概率最大的一個HHM即可。

圖3是反正弦(Arcsine)算法和直接反正切算法以及反正切加相位解模糊算法在有噪聲情況下的解調效果對比圖，可以看出，Arcsine算法相位連續性最好，其余兩種算法均出現了不同程度的相位跳變。

圖4是使用Arcsine解調待測物體單擊和移動兩種運動模式下的距離變化信息的實驗結果。

圖5是在軌跡追蹤基礎上識別待測物體單擊和移動兩種運動模式的實驗結果，從圖4和圖5中可以清楚地分辨待測物體的兩種運動模式。