一種非球面在位檢測中的位置誤差標定方法與流程
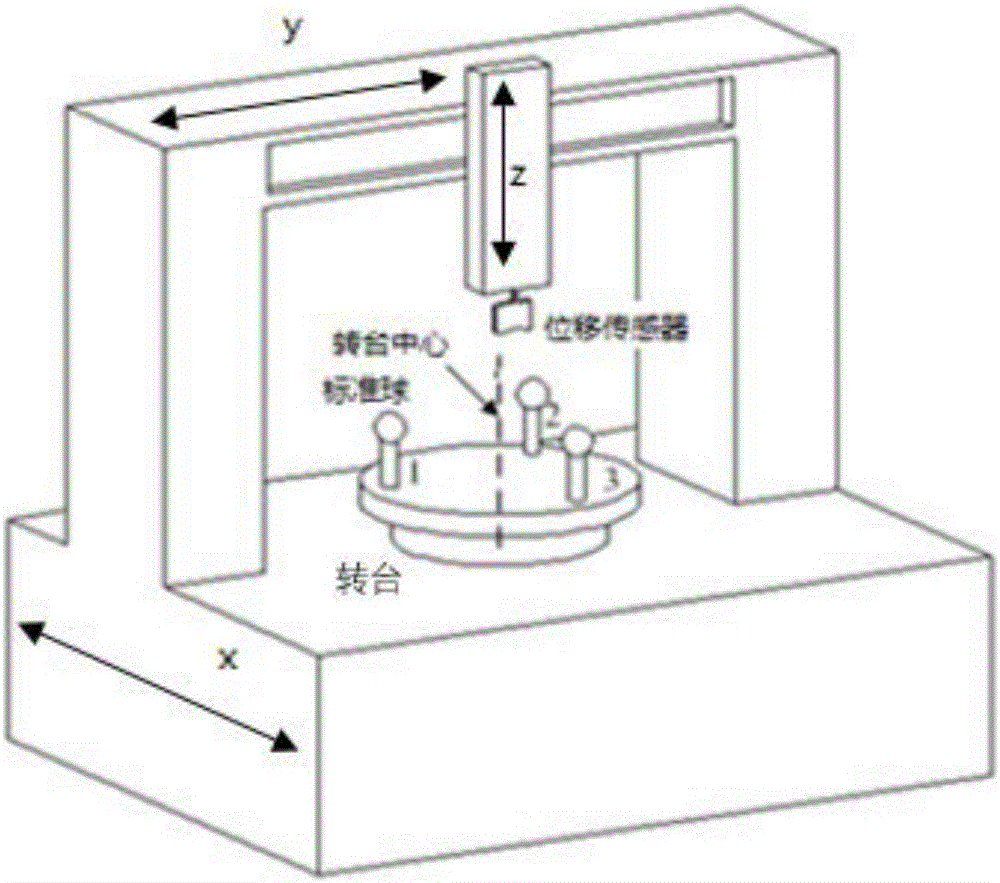
本發明屬于精密測試位置標定技術領域,具體涉及一種非球面在位檢測中的位置標定方法。
背景技術:
非球面鏡片主要應用于光學成像,激光武器,核聚變等場合,由于大口徑非球面體積大,質量高,采用離線手段進行測量在工件搬運方面非常困難,并且在進行二次裝卡時測量坐標系和工件坐標系之間會產生較大的誤差,所以采用在線/在位測量是必不可少的。又因為測量工作對外界環境要求很高,所以一般都在恒溫間中通過專用的測量設備完成,因而大口徑非球面在位測量的技術一直是一個難點。
傳統的非球面測量路徑有如下兩種:子午線式路徑規劃和圓周式路徑規劃,子午線式路徑規劃是對非球面的母線進行測量,即要求每條測量路徑都通過非球面中心;而圓周式路徑規劃則是以非球面中心為基準,沿著x方向每隔一段距離,轉臺旋轉一周進行測量。可以看出,無論是采用哪種路徑進行非球面面型檢測,中點位置的尋找都是至關重要的。
相比于離線測量系統,目前的在位系統都較為簡單,默認轉臺中心和工件中心完全重合,而在實際情況中,由于外界振動和轉臺徑向跳動的影響,會使兩者具有一定的偏移,并且由于位移傳感器的裝卡問題,測量坐標系和轉臺坐標系也無法完全重合。這兩種誤差在后續的測量過程中,特別是對工件面型要求較高時就會導致較大的誤差,從而影響測量精度。
技術實現要素:
為了克服上述現有技術的缺點,本發明的目的在于提供一種非球面在位檢測中的位置標定方法,其在測量中同時消除轉臺中心和工件中心的誤差,以及位移傳感器的裝卡誤差,從而獲得更加的測量精度。
為了達到上述目的,本發明采取的技術方案為:
一種非球面在位檢測中的位置標定方法,包括以下步驟:
1)首先采用三點法進行轉臺中心標定:
1.1)將標準球置于轉臺任意位置,利用位移傳感器測量標準球表面上n點的坐標,n≥4,根據坐標擬合出標準球球心坐標所在位置;
1.2)在保證標準球和轉臺相對位置不發生改變的情況下,轉動轉臺m次,m≥2,分別對標準球表面上n點進行測量,擬合出在m個位置時的標準球球心位置;
1.3)通過步驟1.1)和1.2)所擬合出的標準球球心坐標,擬合出轉臺中心坐標;
2)以轉臺中心為基準,進行非球面中心四點標定:
2.1)以步驟1.3)中擬合出的轉臺中心作為非球面中心的初始位置(0,0),在該點處所測得的工件表面的Z坐標為0,即認為此點為工件中心;
2.2)分別測量(0,d)、(d,0)、(0,-d)、(-d,0)點處工件表面的Z坐標,記做Z(0,d),Z(d,0),Z(0,-d)和Z(-d,0);
2.3)將點Z(0,d)帶入非球面方程中,
R——非球面頂點曲率半徑;
K——非球面系數;
把x設為0,計算出y的值,記做YZ(0,d);同理,帶入Z(d,0),Z(0,-d)和Z(-d,0)的值,在帶入Z(d,0),和Z(-d,0)時將y設0計算x,計算出XZ(d,0),-|YZ(0,-d)|和-|XZ(-d,0)|,并以(XZ(d,0)-|XZ(-d,0)|,YZ(0,d)-|YZ(0,-d)|,)為新的工件中心進行迭代計算,直到前一次和后一次所計算出來的工件中心位置之差小于ε,就認為該點位置為實際的工件中心;
其中,設測量精度要求為k,非球面口徑為φ,則ε根據式(2)算出,
3)測量非球面的面型數據,通過對測量數據進行處理,計算出標定的殘余誤差并對測量結果進行優化:
3.1)轉臺中心標定誤差:
分析步驟1.3)中轉臺中心擬合的殘余誤差在非球面檢測中所造成的影響:在轉臺坐標系中,真實的轉臺中心坐標為(0,0),而經過步驟1.3)擬合之后的轉臺中心為(m,n),那么采用子午線測量法,在非球面測量中,因為轉臺中心而導致的誤差為:
elo=f(r×cos(θ+180°),r×sin(θ+180°))-f(ρ×cos(θ+180°-γ),ρ×sin(θ+180°+γ)) (3)
其中:
γ=arcsin(n/ρ);
3.2)工件中心與轉臺中心的偏差分析:
分析步驟2.3)中工件中心標定的誤差所造成的影響,非球面方程簡化為
z'=f(x',y') (4)
理論上工件中心為(xo',y0'),但是實際上,經過標定出來的轉臺中心為(x',y'),所以工件中心標定的誤差為:
ewc=f(x',y')-f(x-x0',y-y0') (5)
3.3)非球面半徑R的誤差:
非球面頂點曲率半徑R的加工誤差也會對測量結果的評價產生影響,所以實際的曲率半徑R應為R+ΔR;
3.4)接下來進行計算,設非球面鏡中心的坐標為(xo,y0,z0),而所標定出的轉臺中心距離實際轉臺中心的距離為(m,n),非球面的實際頂點曲率半徑為R+ΔR,原始測量數據為(xi',yi',zi'),
考慮到標定出的轉臺中心與實際轉臺中心之間的誤差,帶入測量數據并將其分解到X,Y,Z三個方向,得到處理后的數據(xi”,yi”,zi”):
再帶入非球面中心真實坐標,得到:
接下來加入非球面曲率半徑誤差,得到:
zi-f(xi,yi,ΔR)=0 (8)
其中
式(9)中,c=1/(R+ΔR);
但是參數是未知的,所以在實際應用中,用使上式偏差最小的參數來代替,
要使上式最小,則要使其各項參數的一階偏導數為零,所以對其求偏導,之后將測量數據帶入求偏導之后的方程
采用牛頓法對其進行求解就精確的求出上述各項誤差,從而提高測量精度。
本發明的有益效果為:利用位移傳感器對非球面進行檢測,通過對標準球和非球面表面的測量和計算,完成了非球面在位測量中傳感器的位置標定和非球面位姿誤差的定量分析,從而實現測量坐標系,工件坐標系,轉臺坐標系之間的統一,減小了測量誤差。并且除標準球外不需要使用任何額外的設備,系統簡單,易于實現。
附圖說明
圖1為轉臺中心標定示意圖。
圖2為標準球表面采點路徑規劃示意圖。
圖3為標準球球心擬合轉臺中心示意圖。
圖4為四點定心原理圖。
圖5為四點定心流程圖。
圖6為轉臺中心標定誤差示意圖。
具體實施方式
下面結合附圖對本發明作詳細描述。
一種非球面在位檢測中的位置標定方法,包括以下步驟:
1)首先采用三點法進行轉臺中心標定:
1.1)參照圖1,轉臺中心標定系統由位移傳感器和標準球組成,傳感器安裝在三坐標機床的Z軸上,方向與z軸負方向一致,將標準球置于轉臺上任意位置,記為位置1,已知標準球方程為
(x-x0)2+(y-y0)2+(z-z0)2=R2 (12)
球心坐標為(x0,y0,z0),所以理論上測得球面上4點就能夠通過式(2)擬合出標準球球心的坐標;
但是由于測量存在誤差,所以需要測量大量數據來進行標準球球心坐標擬合,具體過程為:先進行標準球表面采點路徑規劃,參照圖2,傳感器在標準球表面按照1→2→…→9→2的路徑進行移動,其中在每段上均勻采集10個點,之后對這些點采用最小二乘法進行球心擬合;
1.2)在保證標準球和轉臺相對位置不發生改變的情況下,轉動轉臺m次(m≥2),同樣通過步驟1.1)的方法擬合出標準球球心坐標;
1.3)通過步驟1.1)和1.2)所擬合出的標準球球心坐標,采用最小二乘法擬合出轉臺中心坐標,原理如圖3所示;
2)以轉臺中心為基準,進行非球面中心四點標定,理論上在在位測量中非球面工件的中心和轉臺中心應該完全重合,但是由于加工中轉臺徑向跳動和外界震動的干擾,會使非球面中心和轉臺中心產生偏差,即在以轉臺中心為原點,對非球面進行測量時,測量路徑無法與母線重合,這樣在評價中就會帶入誤差,故采用四點定心的方法來對非球面中心進行標定,如圖4、圖5所示;
2.1)以步驟1.3)中擬合出的轉臺中心作為非球面中心的初始位置(0,0),在該點處所測得的工件表面的Z坐標為0,即認為此點為工件中心;
2.2)分別測量(0,d)、(d,0)、(0,-d)、(-d,0)點處工件表面的Z坐標,因為在加工中轉臺徑向跳動和外界振動的干擾,4點的Z坐標會有所區別,把這四點的Z坐標記做Z(0,d),Z(d,0),Z(0,-d)和Z(-d,0);
2.3)將點Z(0,d)帶入非球面方程中,
R——非球面頂點曲率半徑;
K——非球面系數;
把x設為0,計算出y的值,記做YZ(0,d);同理,帶入Z(d,0),Z(0,-d)和Z(-d,0)的值,在帶入Z(d,0),和Z(-d,0)時將y設0計算x,計算出XZ(d,0),-|YZ(0,-d)|和-|XZ(-d,0)|,并以(XZ(d,0)-|XZ(-d,0)|,YZ(0,d)-|YZ(0,-d)|,)為新的工件中心進行迭代計算,直到前一次和后一次所計算出來的工件中心位置之差小于ε,就認為該點位置為實際的工件中心;
其中,設測量精度要求為k,非球面口徑為φ,則ε根據式(2)算出,
3)測量非球面的面型數據,通過對測量數據進行處理,計算出標定的殘余誤差并對測量結果進行優化,理論上一個工件在空間中的擺放位置有6項自由度,但由于轉臺在運行中C軸一般較為平穩,不會產生偏擺,所以工件所產生的傾斜很小,誤差可以被忽略,所以別針對工件和轉臺中心的偏差,傳感器和工件中心的偏差,以及非球面曲率半徑誤差進行分析,
3.1)轉臺中心標定誤差:
由于傳感器誤差和標準球面型精度的影響,在步驟1)中采用標準球標定出來的轉臺中心必然會有一定的偏差,如圖6所示,
設實際的轉臺中心為(0,0),而由于在測量坐標系中轉臺位置是通過擬合而來,存在一定誤差,所以認為所標定出的轉臺中心相對于實際轉臺中心的位置為(m,n),因為采用子午線式測量,每次沿x方向測量一條母線然后轉過θ角度再進行下一次測量,理論上在測頭移動到-r點時測得的應該就是(r×cos(θ+180°),r×sin(θ+180°))點處的坐標,但是當存在誤差(m,n)時,所測量的坐標點為(ρ×cos(θ+180°-γ),ρ×sin(θ+180°+γ))
其中:
γ=arcsin(n/ρ)
所以,由于傳感器標定不對中所造成的誤差為
elo=f(r×cos(θ+180°),r×sin(θ+180°))-f(ρ×cos(θ+180°-γ),ρ×sin(θ+180°+γ)) (3)
3.2)工件中心與轉臺中心的偏差分析:
非球面方程可以簡化為
z'=f(x',y') (4)
理論上,轉臺中心的坐標為(xo',y0'),且在在位測量系統中,工件中心應與轉臺中心重合,但是實際上,由于轉臺徑向跳動和外界振動的影響,兩者之間會存在一定的偏差,(x,y)為測量點的橫縱坐標,所以因為轉臺和非球面的中心偏差導致的誤差為:
ewc=f(x',y')-f(x-x0',y-y0') (5)
3.3)非球面半徑R的誤差:
非球面頂點曲率半徑R的加工誤差也會對測量結果的評價產生影響,所以設實際的曲率半徑R為R+ΔR;
3.4)接下來進行計算,設非球面鏡中心的坐標為(xo,y0,z0),而所標定出的轉臺中心距離實際轉臺中心的距離為(m,n),非球面的實際頂點曲率半徑為R+ΔR,原始測量數據為(xi',yi',zi'),
以二次非球面為例,高次非球面同理可得,考慮到標定出的轉臺中心與實際轉臺中心之間的誤差,帶入測量數據并將其分解到X,Y,Z三個方向,得到處理后的數據(xi”,yi”,zi”):
再帶入非球面中心真實坐標,得到:
接下來加入非球面曲率半徑誤差,得到:
zi-f(xi,yi,ΔR)=0 (8)
其中
式(11)中,c=1/(R+ΔR);
但是參數是未知的,所以在實際應用中,用使式(9)最小的參數來代替,
要使式(10)最小,則要使其各項參數的一階偏導數為零,所以先對式(10)求偏導,之后將測量數據帶入式(11):
最后在matlab中對方程組采用牛頓法進行求解,就能計算出上述的所有誤差,從而對測量結果進行優化。
- 還沒有人留言評論。精彩留言會獲得點贊!