液壓振動臺激振力三折線對數分析方法與流程
本發明涉及振動試驗臺技術領域,特別是涉及一種液壓振動臺激振力三折線對數分析方法。
背景技術:
振動試驗臺是現代產品研發的一個重要技術手段。由于振動試驗臺的激振力比較大,特別是液壓振動臺最大激振力可以達到數千kN,廣泛用于地震模擬試驗、道路模擬試驗機以及航空航天產品的振動環境模擬等,為了避免振動試驗臺振動對環境的影響,確保試驗設施周邊建筑物的安全,工程設計人員需要了解振動臺激振力的頻率特性。在以往的工程設計中,由于缺少激振力分析的基本方法,只能憑經驗來估計,使得結構工程往往不經濟,而且也無法確保結構的安全。
技術實現要素:
本發明的目的提供一種液壓振動臺激振力三折線對數分析方法,已解決上述現有技術中存在的技術問題。
為實現本發明的目的,本發明提供了一種液壓振動臺激振力三折線對數分析方法,所述激振力通過下述公式計算得出,
F(f)=m·a(f) (式1)
式中,F(f)為激振力;m為試驗臺運動部分質量;a(f)為對應頻率f的加速度值。
其中,為了計算試驗臺的振動加速度值,在選擇振動試驗臺時,需要先確定最大位移Umax、最大速度Vmax和最大加速度Amax,
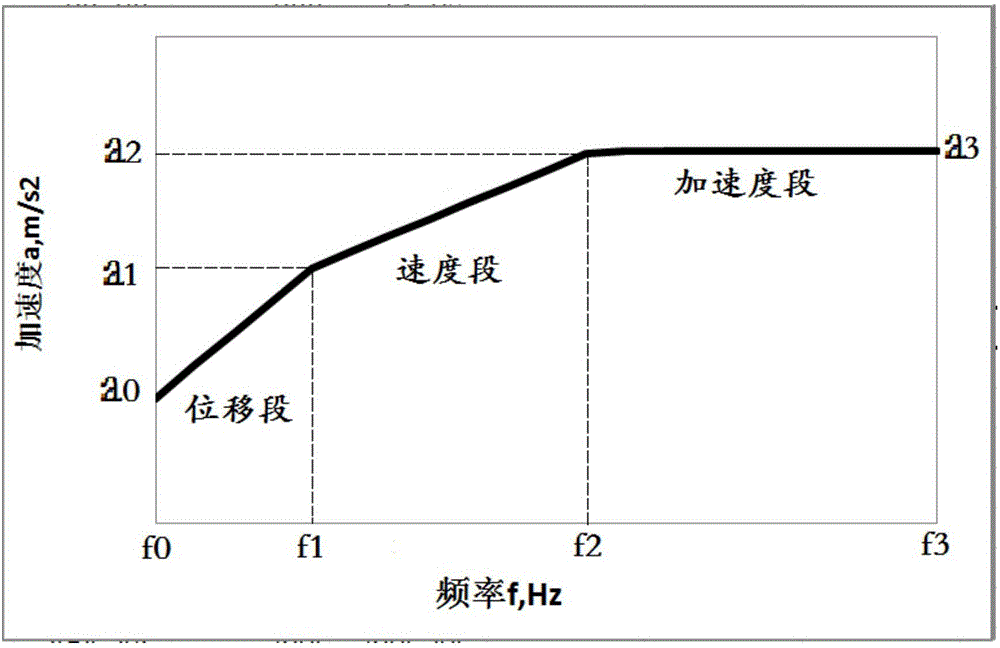
假定試驗臺加速度曲線在雙對數坐標下呈三折線曲線,其中,橫坐標為頻率f,縱坐標為加速度a,對于這樣的三折線曲線,需要確定四個端點,分別為(f0,a0),(f1,a1),(f2,a2),(f3,a3),上述四個端點連成一個三折線,也就是將液壓振動臺可分為三個加速度區間:
低頻部分的位移控制區段,a1=Umaxω2
中頻部分的速度控制區段,a2=Vmaxω
高頻部分的加速度控制區段,a3=Amax
式中,ω=2πf為圓頻率
計算每個區段的斜率ki以及截距ci,公式如下:
yi=kixi+ci
yi=lgai,
xi=lgfi,
ci=lgai-kilgfi
i=0,1,2,3
于是,lgai=kilgfi+ci
a1=2πf1·Vmax=(2πf1)2·Umax
u1=Umax
其中,高頻部分的加速度控制區段為平直段,因此,
a2=a3=Amax
c3=lgAmax
k3=0
根據上述計算結果,就可以得到全頻域的通式:
計算出加速度a(f)后,按照(式1)即可計算激振力。
與現有技術相比,本發明的有益效果為,根據振動試驗臺的結構特性和工作原理,參考牛頓定律建立了一個振動試驗臺激振力三折線對數分析方法,可以方便、準確的分析振動試驗臺的激振力,為試驗臺基礎設計提供有效的振動荷載依據,為結構工程安全和試驗設施的正常使用提供可靠的保障。
附圖說明
圖1為本發明實施例試驗臺加速度曲線圖;
圖2為本發明實施例試驗臺三參數控制線圖;
具體實施方式
以下結合附圖和具體實施例對本發明作進一步詳細說明。應當理解,此處所描述的具體實施例僅僅用以解釋本發明,并不用于限定本發明。
根據振動試驗臺的結構特性和工作原理,參考牛頓定律建立了一個振動試驗臺激振力三折線對數分析方法,可以方便、準確的分析振動試驗臺的激振力,為試驗臺基礎設計提供有效的振動荷載依據,為結構工程安全和試驗設施的正常使用提供可靠的保障。
該方法是首次提出,其分析結果已在《建筑振動荷載規范》中應用。
振動試驗臺的主要目的是給被試件提供有效的作用力。因此振動臺的主要技術指標包括激振力,振動位移,振動速度和振動加速度等。由于受振動臺的作動器結構特性的制約,試驗臺在整個試驗頻率區間的激振力并不相等。振動試驗臺是一種開敞式加載的裝置,激振力表現為慣性力,當被試件質量確定后,激振力就與加速度成正比。所以在低頻區段受到試驗臺作動器活塞行程和液壓油流速的限制,運動加速度達不到最大值。可見在低頻段振動臺激振力大小由位移決定,中頻段激振力大小由速度決定,高頻部分激振力則由加速度控制。
如圖2所示,為振動臺的三參數控制線示意圖。
為了計算振動試驗臺的激振力首先需要確定試驗臺的振動加速度,依據牛頓第二定律可以推算出振動試驗臺的慣性力,也就是激振力,即
F(f)=m·a(f) (式1)
式中,F(f)為激振力;m為試驗臺運動部分質量;a(f)為對應頻率f的加速度值。
為了計算試驗臺的振動加速度包絡值,在選擇振動試驗臺時,需要先確定最大位移Umax,最大速度Vmax和最大加速度Amax。參考振動分析方法中常用的雙對數圖形,假定試驗臺曲線在雙對數坐標下呈線性,如圖1所示。
對于這樣的三折線曲線,需要確定四個端點,分別為(f0,a0),(f1,a1),(f2,a2),(f3,a3),上述四個端點連成一個三折線,也就是將液壓振動臺可分為三個加速度區間:
低頻部分的位移控制區段,a1=Umaxω2
中頻部分的速度控制區段,a2=Vmaxω
高頻部分的加速度控制區段,a3=Amax
式中,ω=2πf為圓頻率
按照幾何代數方法,不難計算出該曲線的函數式。計算每個區段的斜率ki以及截距ci,公式如下:
yi=kixi+ci
yi=lgai,
xi=lgfi,
ci=lgai-kilgfi
i=0,1,2,3
于是,lgai=kilgfi+ci
a1=2πf1·Vmax=(2πf1)2·Umax
u1=Umax
其中,高頻部分的加速度控制區段為平直段,因此,
a2=a3=Amax
c3=lg Amax
k3=0
根據上述計算結果,就可以得到全頻域的通式:
計算出加速度a(f)后,按照(式1)即可計算激振力。
計算實例
在0.01-100Hz頻率范圍,已知最大位移Umax=150mm,最大速度Vmax=1.2m/s,最大加速度amax=10m/s2,且a=0.01m/s2,(當f=0.01Hz時)。振動臺運動部分質量為m=800kg,最大激振力為Fmax=20kN。計算f=2.5Hz處的激振力。
解:
a1=2πf1·Vmax=2π×1.273×1.2=9.598(m/s2)
a2=a3=Amax=20(m/s2)
c1=lga1-k1lgf1=lg9.598-1.332lg1.273=0.8336
c2=lga2-k2lgf2=lg20-1.000lg2.653=0.8774
激振力為
F=m·a(f)=800×100.8774×2.51.0=15.08(kN)<Fmax=20kN
滿足激振力的要求。
以上所述僅是本發明的優選實施方式,應當指出的是,對于本技術領域的普通技術人員來說,在不脫離本發明原理的前提下,還可以做出若干改進和潤飾,這些改進和潤飾也應視為本發明的保護范圍。
- 還沒有人留言評論。精彩留言會獲得點贊!