一種非侵入式的穩態負荷監測方法與流程
本發明涉及電力系統負荷監測的技術領域,特別是涉及非侵入式的穩態負荷監測方法。
背景技術:
負荷監測是指通過實時采集負荷的電氣參數,監測其運行狀態。負荷監測不僅能監測單個負荷,還可以從整個系統的全局角度出發,了解各類負荷的狀態參數、用電量和用電時間,從而幫助決策者合理地分配電能,使整個電力系統始終處于高效的運行狀態,這在強調節能減排的今天具有重要的意義。
目前的負荷監測手段大都是侵入式的,即針對系統內的每類負荷都安裝傳感器,單獨監測其運行狀態。
侵入式負荷監測需要大量的硬件設備,在采購、安裝、維護時都會耗費大量成本,又因為每個檢測設備都是一個數據源,因此在負荷較多時,數據處理和分析都將變得比較困難。
因此希望有一種非侵入式的穩態負荷監測方法可以克服或至少減輕現有技術的上述缺陷。
技術實現要素:
本發明的目的在于提供一種非侵入式的穩態負荷監測方法來實現僅在電力系統的總端安裝監測裝置,通過采集總端的電氣參數,分析得到系統內各類負荷的含量和狀態。這樣可以省去大量的監測設備,減少數據處理與分析工作,同時變相實現對系統內每類負荷的狀態監測
為實現上述目的,本發明提供一種非侵入式的穩態負荷監測方法,所述非侵入式的穩態負荷監測方法建立穩態過程的非侵入式負荷分解模型,供電電壓采用的是50HZ的工頻周期電壓,因此電流波形也必定是50HZ的周期量,則依據傅里葉分析理論,單個負荷在某次測量中的電流可分解為:
it=α1·sin(ωt+θ1)+α2·sin(2·ωt+θ2)+…+αk·sin(k·ωt+θk) (1)
公式(1)中第一項為基波,其余項為各次諧波,其中α為基波或各次諧波的幅值,ω為基波角頻率,工頻時為2π·50,θ為基波或各次諧波在此次測量中的初相角,構成了周期量的三要素幅值、頻率和相位角;
同一個負荷,對其電流進行多次測量,基波和各次諧波的幅值是恒定的,頻率由諧波次數反映也是恒定的,由于測量開始記錄的波形位置不恒定,因此相位角不恒定,對于一個包含數量大于1次的諧波的穩態電流來說,其能有固定的波形,是因為基波和各次諧波有恒定的幅值,且基波和各次諧波間有固定的相對位置,這種相對位置的信息就在每次測量的相位角中,找到基波與各次諧波間的相位差,就可依據幅值重構出原始波形;
因為不同諧波的頻率不相同,所以不能直接求相位差,為此設基波相位角為參考相位,采用換元法,另x=ωt+θ1,則有ωt=x-θ1,代入(1)式中的第j次諧波則有:
it(j)=αj·sin(j·(x-θ1)+θj)=αj·sin(j·x+(-j·θ1+θj)) (2)
公式(2)僅針對本次測量,設除本次測量外的任意一次測量的基波相位角為θc,則有x=ωt+θc,代入式(2)并推廣到公式(1)有公式(3):
其中:
Δθj=mod(-j·θ1+θj,2π) (4)
公式(3)即為單負荷穩態電流的完備數學模型,定義公式(4)中的Δθj為諧波位置角,其決定了第j次諧波與基波的相對位置,和幅值αj共同固化了整個波形的形狀;θc為基波相位角,其決定了整個波形在時間軸上的移動,但不影響波形的形狀;θ1和θj分別為某次訓練測量的基波和諧波的相位角,用于計算Δθj;
由于Δθj是固定值,可由訓練測量的相位角計算得來,因此要分解并重構任意一次實測的電流波形,僅需計算其基波相位角θc即可;
由疊加定理可知,n類負荷電流組成的總負荷電流可用下式表示:
It=β1it1+β2it2+…+βnitn (5)
上式(5)中,it為單負荷電流,β為各類負荷的權重系數,是相應負荷的數量,依據公式(3),將It表示為矩陣形式:
上式(6)中,αI和θI分別為多負荷電流It的幅值和相位,α為各類負荷的基波或諧波的幅值,Δθ和θC分別為各類負荷的諧波位置角和基波相位角,β為權重系數,對于分解過程,αI、θI、α和Δθ可由訓練或諧波分析得出為已知量,θC和β為待求量。
優選地,在同一次測量中,對于同類負荷,由于具有相同的容感性,所述基波相位角θC是相同的,直接乘所述權重系數β表示多個此類負荷同時工作;而對于不同負荷,由于容感性不同,所述基波相位角θC也是不同的,在總電流波形中,所述基波相位角θC決定了各類負荷電流波形的相對位置,而各類負荷電流波形中,所述諧波位置角Δθ決定了基波和各次諧波間的相對位置,根據所述已知量αI、θI、α和Δθ,求解未知量所述基波相位角θC和所述權重系數β,完成了多負荷電流波形的分解,公式(6)為多負荷穩態電流的完備數學模型,其表示為:
It=A·B (7)
公式(7)中,It=(αI1∠θI1,αI2∠θI2,…αIk∠θIk)T,為諧波分析得到的總負荷電流的矩陣形式,A為特征參數矩陣,其包含了單個負荷電流波形的形狀信息和不同負荷電流波形的位置信息,B為權重系數矩陣,其包含了總電流波形中各個負荷的數量。
優選地,穩態過程的非侵入式負荷分解,根據測量得到的總負荷電流矩陣It,依據矩陣A求出矩陣B,由于矩陣A中也有未知量所述基波相位角θC,因此分解過程可轉化為求解如下未知數向量:
由于實際測量中都存在誤差,因此公式(7)不能求出精確解析解,為此建立目標函數:
上式中為要求解的未知數向量,‖·‖2為L2范數,βmax為對應負荷數量的估計或實際最大值,總負荷穩態電流的分解轉化為求解使公式(9)取得最小值的向量及求解:
用全局尋優算法求解公式(10),求得使電流負荷波形最優化匹配,完成穩態過程的非侵入式負荷分解。
優選地,穩態負荷分解方法的流程分為兩部分:訓練和實測分解,所述訓練方法是求解特征參數矩陣中的幅值α和諧波位置角Δθ,所述實測分解方法是對測量得到的多負荷電流波形進行分解。
優選地,所述訓練方法包括以下步驟:
(1)測量系統內所有類別負荷的單負荷電流穩態波形;
(2)諧波分析,得到每類負荷電流基波和各次諧波的幅值及相位;
(3)計算所述諧波位置角Δθ;
(4)將各類負荷的幅值α和諧波位置角Δθ填入特征參數矩陣A。
優選地,所述實測分解方法包括以下步驟:
(1)測量某一時刻系統的總負荷電流波形,將其作為待分解波形;
(2)諧波分析,得到總電流基波和各次諧波的幅值αI和相位θI;
(3)形成總負荷電流It的矩陣形式,和訓練算法得到的A一起代入公式(9),完善目標函數;
(4)用全局尋優算法針對公式(10)進行全局尋優;
(5)得到各類負荷含量,完成穩態分解。
本發明的非侵入式的穩態負荷監測方法能在電力系統總端只安裝一個傳感器的情況下,精確的測得系統內各類負荷的含量和狀態,本發明的非侵入式的穩態負荷監測方法能夠極大地節省硬件設備的采購、安裝、維護等成本,減少傳感器的數量,降低數據處理難度,是一種優良的負荷監測算法。
附圖說明
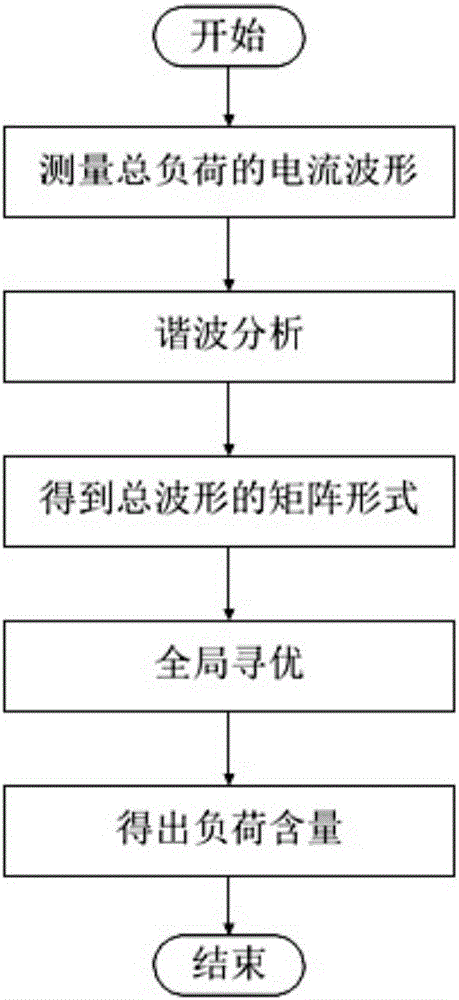
圖1是進行穩態過程的非侵入式負荷分解的訓練方法流程圖。
圖2是進行穩態過程的非侵入式負荷分解的實測分解方法流程圖。
圖3是待分解實測波形。
具體實施方式
為使本發明實施的目的、技術方案和優點更加清楚,下面將結合本發明實施例中的附圖,對本發明實施例中的技術方案進行更加詳細的描述。在附圖中,自始至終相同或類似的標號表示相同或類似的元件或具有相同或類似功能的元件。所描述的實施例是本發明一部分實施例,而不是全部的實施例。下面通過參考附圖描述的實施例是示例性的,旨在用于解釋本發明,而不能理解為對本發明的限制。基于本發明中的實施例,本領域普通技術人員在沒有作出創造性勞動前提下所獲得的所有其他實施例,都屬于本發明保護的范圍。下面結合附圖對本發明的實施例進行詳細說明。
在本發明一寬泛實施例中:所述非侵入式的穩態負荷監測方法建立穩態過程的非侵入式負荷分解模型,供電電壓采用的是50HZ的工頻周期電壓,因此電流波形也必定是50HZ的周期量,則依據傅里葉分析理論,單個負荷在某次測量中的電流可分解為:
it=α1·sin(ωt+θ1)+α2·sin(2·ωt+θ2)+…+αk·sin(k·ωt+θk) (1)
公式(1)中第一項為基波,其余項為各次諧波,其中α為基波或各次諧波的幅值,ω為基波角頻率,工頻時為2π·50,θ為基波或各次諧波在此次測量中的初相角,構成了周期量的三要素幅值、頻率和相位角;
同一個負荷,對其電流進行多次測量,基波和各次諧波的幅值是恒定的,頻率由諧波次數反映也是恒定的,由于測量開始記錄的波形位置不恒定,因此相位角不恒定,對于一個包含數量大于1次的諧波的穩態電流來說,其能有固定的波形,是因為基波和各次諧波有恒定的幅值,且基波和各次諧波間有固定的相對位置,這種相對位置的信息就在每次測量的相位角中,找到基波與各次諧波間的相位差,就可依據幅值重構出原始波形;
因為不同諧波的頻率不相同,所以不能直接求相位差,為此設基波相位角為參考相位,采用換元法,另x=ωt+θ1,則有ωt=x-θ1,代入(1)式中的第j次諧波則有:
it(j)=αj·sin(j·(x-θ1)+θj)=αj·sin(j·x+(-j·θ1+θj)) (2)
公式(2)僅針對本次測量,設除本次測量外的任意一次測量的基波相位角為θc,則有x=ωt+θc,代入式(2)并推廣到公式(1)有公式(3):
其中:
Δθj=mod(-j·θ1+θj,2π) (4)
公式(3)即為單負荷穩態電流的完備數學模型,定義公式(4)中的Δθj為諧波位置角,其決定了第j次諧波與基波的相對位置,和幅值αj共同固化了整個波形的形狀;θc為基波相位角,其決定了整個波形在時間軸上的移動,但不影響波形的形狀;θ1和θj分別為某次訓練測量的基波和諧波的相位角,用于計算Δθj;
由于Δθj是固定值,可由訓練測量的相位角計算得來,因此要分解并重構任意一次實測的電流波形,僅需計算其基波相位角θc即可;
由疊加定理可知,n類負荷電流組成的總負荷電流可用下式表示:
It=β1it1+β2it2+…+βnitn (5)
上式(5)中,it為單負荷電流,β為各類負荷的權重系數,是相應負荷的數量,依據公式(3),將It表示為矩陣形式:
上式(6)中,αI和θI分別為多負荷電流It的幅值和相位,α為各類負荷的基波或諧波的幅值,Δθ和θC分別為各類負荷的諧波位置角和基波相位角,β為權重系數,對于分解過程,αI、θI、α和Δθ可由訓練或諧波分析得出為已知量,θC和β為待求量。
在同一次測量中,對于同類負荷,由于具有相同的容感性,所述基波相位角θC是相同的,直接乘所述權重系數β表示多個此類負荷同時工作;而對于不同負荷,由于容感性不同,所述基波相位角θC也是不同的,在總電流波形中,所述基波相位角θC決定了各類負荷電流波形的相對位置,而各類負荷電流波形中,所述諧波位置角Δθ決定了基波和各次諧波間的相對位置,根據所述已知量αI、θI、α和Δθ,求解未知量所述基波相位角θC和所述權重系數β,完成了多負荷電流波形的分解,公式(6)為多負荷穩態電流的完備數學模型,其表示為:
It=A·B (7)
公式(7)中,It=(αI1∠θI1,αI2∠θI2,…αIk∠θIk)T,為諧波分析得到的總負荷電流的矩陣形式,A為特征參數矩陣,其包含了單個負荷電流波形的形狀信息和不同負荷電流波形的位置信息,B為權重系數矩陣,其包含了總電流波形中各個負荷的數量。
穩態過程的非侵入式負荷分解,根據測量得到的總負荷電流矩陣It,依據矩陣A求出矩陣B,由于矩陣A中也有未知量所述基波相位角θC,因此分解過程可轉化為求解如下未知數向量:
由于實際測量中都存在誤差,因此公式(7)不能求出精確解析解,為此建立目標函數:
上式中為要求解的未知數向量,‖·‖2為L2范數,βmax為對應負荷數量的估計或實際最大值,總負荷穩態電流的分解轉化為求解使公式(9)取得最小值的向量及求解:
用全局尋優算法求解公式(10),求得使電流負荷波形最優化匹配,完成穩態過程的非侵入式負荷分解。
穩態負荷分解方法的流程分為兩部分:訓練和實測分解,所述訓練方法是求解特征參數矩陣中的幅值α和諧波位置角Δθ,所述實測分解方法是對測量得到的多負荷電流波形進行分解。
所述訓練方法包括以下步驟:
(1)測量系統內所有類別負荷的單負荷電流穩態波形;
(2)諧波分析,得到每類負荷電流基波和各次諧波的幅值及相位;
(3)計算所述諧波位置角Δθ;
(4)將各類負荷的幅值α和諧波位置角Δθ填入特征參數矩陣A。
所述實測分解方法包括以下步驟:
(1)測量某一時刻系統的總負荷電流波形,將其作為待分解波形;
(2)諧波分析,得到總電流基波和各次諧波的幅值αI和相位θI;
(3)形成總負荷電流It的矩陣形式,和訓練算法得到的A一起代入公式(9),完善目標函數;
(4)用全局尋優算法針對公式(10)進行全局尋優;
(5)得到各類負荷含量,完成穩態分解。
分別選取負荷1、負荷2、負荷3、負荷4、負荷5,每類負荷設開關兩個穩定狀態,將5類負荷的狀態隨機組合(如負荷1、2、3開啟,負荷4、5關閉),取15種組合測量其總的穩態電流波形,分別表示為S1,S2,…S15,其實測波形如圖3所示,首先用高精度FFT算法對分別對5類負荷和上述15組多負荷電流波形進行諧波分析,得到αI、θI、a、Δθ,代入分解模型式(6),完善目標函數式(9),繼而進行全局尋優,求解權重系數β和基波相位角θC。
用遺傳算法對其進行全局尋優,取最后一代種群中最優的個體作為尋優結果,分解結果如表1所示,表中βi和θCi分別為五類負荷的權重系數和基波相位角。
表1分解結果
經過與事先記錄的負荷開關狀態的對比,以上15組分解得到的權重系數全部正確,權重系數的尋優正確率達到100%。由此說明,此穩態算法精確地測得了系統中各負荷的含量。
最后需要指出的是:以上實施例僅用以說明本發明的技術方案,而非對其限制。盡管參照前述實施例對本發明進行了詳細的說明,本領域的普通技術人員應當理解:其依然可以對前述各實施例所記載的技術方案進行修改,或者對其中部分技術特征進行等同替換;而這些修改或者替換,并不使相應技術方案的本質脫離本發明各實施例技術方案的精神和范圍。
- 還沒有人留言評論。精彩留言會獲得點贊!