基于巖石物理模型的含氣砂巖儲層地震響應數值模擬方法與流程
本發明涉及地質
技術領域:
,尤其涉及一種基于巖石物理模型的含氣砂巖儲層地震響應數值模擬方法。
背景技術:
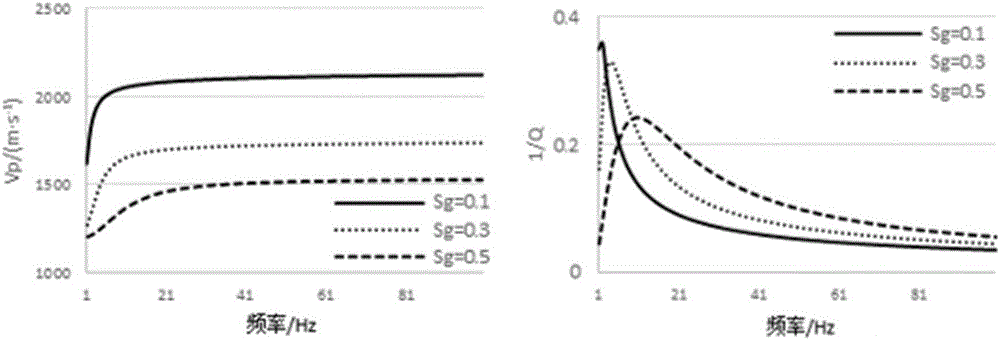
:目前基于巖石物理模型的地震波衰減特征分析多停留在對反射系數討論,而傳統波動方程正演模擬中模型的建立多是基于對實際地層中地震波速度的估計,因此由于增加了人為干預的主觀性變得不準確,基于巖石物理模型建立的地質模型更加符合實際,因此巖石物理模型與波動方程正演的結合是數值模擬方法必然的發展趨勢。斑塊飽和模型是一種飽含流體,且部分含氣部分含水的巖石物理模型,它能夠用來模擬常規含氣砂巖的巖石物理特征;黏滯彌散波動方程主要用來模擬含流體介質的地震響應特征。技術實現要素:本發明的目的在于解決上述現有技術存在的缺陷,提供一種基于巖石物理模型的含氣砂巖儲層地震響應數值模擬方法,能夠有效地將巖石物理模型的地球物理特征表現出來,更加直觀且準確地給出常規含氣砂巖的地震響應特征。未達到上述目的,本發明采用如下方案:基于巖石物理模型的含氣砂巖儲層地震響應數值模擬方法,巖石物理模型為空間周期排列球狀斑塊飽和模型;該方法包括以下步驟:根據Wood定律計算低頻情況下孔隙流體的有效體積模量,從而利用Gassmann方程得到巖石等效體積模量;高頻下首先根據Gassmann方程計算不同流體的體積模量,再利用Hill理論計算巖石體積模量;利用Johnson理論給出動態體積模量,進而計算地震縱波復速度;根據Carcoine衰減理論得到地震P波相速度和品質因子的頻散關系,并將其引入頻率波數域得到復波數,結合利用頻變反射系數公式與子波褶積得到的初始波場,代入二維黏滯彌散波動方程進行數值模擬。進一步地,具體實現過程如下:基于空間周期排列球狀斑塊飽和模型,球體內部飽含氣,外部飽含水,當地震波傳播到斑塊飽和介質時,由于氣和水的存在導致產生了不同的孔隙壓力,利用Biot理論解釋相應的孔隙壓力動態平衡過程,并給出相應的地震波擴散長度:L=Fi/ω---(1)]]>其中ω為角頻率,Fi為擴散系數,i=g,w;其中g代表氣,w代表水:其中,κ為斑塊飽和模型的滲透率,η為孔隙流體的黏滯系數,Mc、Kav根據含流體多孔介質的一些物理屬性給出:Mc(Kf)=KG(Kf)+43μ---(5)]]>式中,Km、Ks、Kf分別為干巖石、固體顆粒和孔隙流體的體積模量,μ為含流體多孔介質的剪切模量,根據Hill理論,假設其余各混合組分的剪切模量都相同,φ為孔隙度,KG(Kf)則根據對應流體體積模量和Gassmann方程算出:當地震波頻率足夠低時,流體之間有足夠的時間來達到孔隙壓力平衡,基于Wood定律可以得到孔隙流體的有效體積模量:KR=(fiKi)-1---(7)]]>其中fi(i=g,w)為介質孔隙中流體的體積分量,這里以氣和水的飽和度代替,Ki(i=g,w)為對應氣和水的體積模量;于是在低頻背景下,根據Gassmann方程計算出巖石的等效體積模量:相對的,當地震波頻率很高時,流體之間沒有時間達到孔隙壓力平衡,此時孔隙中產生的壓力是不均勻的,若假設孔隙壓力不同但均為常數,可根據Gassmann方程首先計算不同流體的體積模量,再根據Hill理論計算高頻下的巖石等效體積模量:KH=Σi=g,wMc(Ki)Si-43μ---(9)]]>根據高頻和低頻下的巖石等效體積模量,求得對應中間頻率時含氣、水巖石的等效體積模量:KD=KH-KH-KL1-θ+θ1+100iωσ/θ2---(10)]]>式中,i為虛數單位,θ和σ可分別根據干巖石、流體的物理性質等求出,這里給出相應的計算公式:θ=KH-KL2KL·σT---(11)]]>σ=(KH-KL)2KH2G2---(12)]]>G=[Σi=g,w(Zi+Qi)Mc(Ki)Σi=g,wφSiKG(Ki)Mc(Ki)]2·SVF---(13)]]>Zi=φ2Kav(Ki)(14)F=(κKHΣi=g,wηiDi)2---(16)]]>上式中,Di(i=g,w)即為對應流體的擴散系數,可由之前提到的Biot理論計算得到,在空間周期排列斑塊飽和模型中,S/V、T可表示為:SV=3Rg2Rw2---(17)]]>T=1κKLφ230Rw3[3ηwgw2+5(ηg-ηw)gggw-3ηggg2]Rg5+5gw[3ηwgw-(2ηw+ηg)gg]Rg2Rw3-15ηwgw(gw-gg)Rg3Rw2-3ηwgw2Rw5---(18)]]>其中:通過上述公式計算得到地震縱波在含氣、含水儲層中傳播的復速度:VR=KD+43μρb---(20)]]>其中,ρb為介質的體密度,式中ρs、ρi分別為固體顆粒和流體的密度,Si為對應的孔隙流體的飽和度;根據Carcoine衰減理論,利用復速度給出地震波在衰減介質中的等效相速度和品質因子:VP=[Re(1VR)]-1---(21)]]>Q=Re(VR2)Im(VR2)---(22)]]>依此得到斑塊飽和介質中地震波相速度和品質因子的頻散關系,利用上述頻散關系,結合二維黏滯-彌散波動方程,進行數值模擬。進一步地,黏滯-彌散波動方程正演的具體實現步驟如下:首先根據二維黏滯-彌散波動方程:∂2u∂t2+γ∂u∂t-η(∂3u∂x2∂t+∂3u∂z2∂t)-v2(∂2u∂x2+∂2u∂z2)=0---(23)]]>上式中,u為質點位移,γ為含流體介質的彌散系數,η為含流體介質的黏滯系數,v為介質中地震波速度,給出方程的簡諧波形式的解:u=ei(kzz+kxx)eiωt---(24)]]>式中,ω為圓頻率,kx、kz分別為x、z方向的波數,單位為1/m,i為虛數單位。將上式代入波動方程有:于是有:kz2=ω2(v2-γη)v4+ω2η2kx2+iω(γv2+ηω2)v4+ω2η2---(26)]]>令kz=k+iα(27)等式兩邊平方得到得k和α關于黏滯彌散系數的表達式;根據Gazdag等的頻率-波數域波場延拓公式:P(z0+dz)=P(z0)eikzdz=P(z0)ei(k+iα)dz---(28)]]>其中,ei(k+iα)dz為相移因子,利用上式進行疊前黏滯-彌散波動方程正演數值模擬;根據斑塊飽和模型中地震波相速度的頻散關系式(21),將其代入計算波數的公式式(26-28)求得相移因子,設計模型對含氣砂巖的地震響應特征進行較準確的分析。本發明基于球狀斑塊飽和模型,能夠較好地描述常規含氣砂巖的巖石物理和地震動力學特征,應用黏滯彌散波動方程理論,引入地震波在傳播時因流體的存在而造成的衰減和能量損失。利用頻率-波數域黏滯彌散波動方程進行正演模擬,能夠有效地將巖石物理模型的地球物理特征表現出來,結合黏滯彌散理論帶來的含流體介質的黏滯特征和彌散特征,能夠更加直觀且準確地給出常規含氣砂巖的地震響應特征。附圖說明圖1地質模型圖2不同含氣飽和度下地震波相速度與逆品質因子的頻散關系曲線圖3不同含氣飽和度下三類砂巖儲層地震響應圖4不同含氣飽和度時下界面反射波頻譜具體實施方式為使本發明的目的、技術方案和優點更加清楚,下面本發明中的技術方案進行清楚、完整地描述,顯然,所描述的實施例是本發明一部分實施例,而不是全部的實施例。基于本發明中的實施例,本領域普通技術人員在沒有作出創造性勞動前提下所獲得的所有其他實施例,都屬于本發明保護的范圍。本發明提供了一種基于巖石物理模型的含氣砂巖儲層地震響應數值模擬方法,該模型為空間周期排列球狀斑塊飽和模型,該方法包括以下步驟:根據Wood定律計算低頻情況下孔隙流體的有效體積模量,從而利用Gassmann方程得到巖石等效體積模量;高頻下首先根據Gassmann方程計算不同流體的體積模量,再利用Hill理論計算巖石體積模量;利用Johnson理論給出動態體積模量,進而計算地震縱波復速度;根據Carcoine衰減理論得到地震P波相速度和品質因子的頻散關系,并將其引入頻率波數域得到復波數,結合利用頻變反射系數公式與子波褶積得到的初始波場,代入二維黏滯彌散波動方程即可進行數值模擬。本發明給出了一種更加貼合實際的含氣砂巖儲層數值模擬方法。以下為具體實現過程:基于空間周期排列球狀斑塊飽和模型,球體內部飽含氣,外部飽含水。當地震波傳播到斑塊飽和介質時,由于氣和水的存在導致產生了不同的孔隙壓力,利用Biot理論解釋相應的孔隙壓力動態平衡過程,并給出相應的地震波擴散長度:L=Fi/ω---(1)]]>其中ω為角頻率,Fi(i=g,w;其中g代表氣,w代表水)為擴散系數:其中,κ為斑塊飽和模型的滲透率,η為孔隙流體的黏滯系數,Mc、Kav則可根據含流體多孔介質的一些物理屬性給出:Mc(Kf)=KG(Kf)+43μ---(5)]]>式中,Km、Ks、Kf分別為干巖石、固體顆粒和孔隙流體的體積模量,μ為含流體多孔介質的剪切模量,根據Hill理論,我們假設其余各混合組分的剪切模量都相同,φ為孔隙度,KG(Kf)則可根據對應流體體積模量和Gassmann方程算出:當地震波頻率足夠低時,流體之間有足夠的時間來達到孔隙壓力平衡,基于Wood定律可以得到孔隙流體的有效體積模量:KR=(fiKi)-1---(7)]]>其中fi(i=g,w)為介質孔隙中流體的體積分量,這里以氣和水的飽和度代替,Ki(i=g,w)為對應氣和水的體積模量。于是在低頻背景下,根據Gassmann方程可以計算出巖石的等效體積模量:相對的,當地震波頻率很高時,流體之間沒有時間達到孔隙壓力平衡,此時孔隙中產生的壓力是不均勻的,若假設孔隙壓力不同但均為常數,可根據Gassmann方程首先計算不同流體的體積模量,再根據Hill理論計算高頻下的巖石等效體積模量:KH=Σi=g,wMc(Ki)Si-43μ---(9)]]>根據高頻和低頻下的巖石等效體積模量,可以求得對應中間頻率時含氣、水巖石的等效體積模量:KD=KH-KH-KL1-θ+θ1+100iωσ/θ2---(10)]]>式中,i為虛數單位,θ和σ可分別根據干巖石、流體的物理性質等求出,這里給出相應的計算公式:θ=KH-KL2KL·σT---(11)]]>σ=(KH-KL)2KH2G2---(12)]]>G=[Σi=g,w(Zi+Qi)Mc(Ki)Σi=g,wφSiKG(Ki)Mc(Ki)]2·SVF---(13)]]>Zi=φ2Kav(Ki)(14)F=(κKHΣi=g,wηiDi)2---(16)]]>上式中,Di(i=g,w)即為對應流體的擴散系數,可由之前提到的Biot理論計算得到。在空間周期排列斑塊飽和模型中,S/V、T可表示為:SV=3Rg2Rw2---(17)]]>T=1κKLφ230Rw3[3ηwgw2+5(ηg-ηw)gggw-3ηggg2]Rg5+5gw[3ηwgw-(2ηw+ηg)gg]Rg2Rw3-15ηwgw(gw-gg)Rg3Rw2-3ηwgw2Rw5---(18)]]>其中:通過上述公式計算得到地震縱波在含氣、含水儲層中傳播的復速度:VR=KD+43μρb---(20)]]>其中,ρb為介質的體密度,式中ρs、ρi分別為固體顆粒和流體的密度,Si為對應的孔隙流體的飽和度。根據Carcoine衰減理論,利用復速度給出地震波在衰減介質中的等效相速度和品質因子:VP=[Re(1VR)]-1---(21)]]>Q=Re(VR2)Im(VR2)---(22)]]>依此即可得到斑塊飽和介質中地震波相速度和品質因子的頻散關系。利用上述頻散關系,結合二維黏滯-彌散波動方程,即可進行數值模擬。下面將介紹黏滯-彌散波動方程正演的具體實現過程。首先根據二維黏滯-彌散波動方程:∂2u∂t2+γ∂u∂t-η(∂3u∂x2∂t+∂3u∂z2∂t)-v2(∂2u∂x2+∂2u∂z2)=0---(23)]]>上式中,u為質點位移,γ為含流體介質的彌散系數,η為含流體介質的黏滯系數,v為介質中地震波速度。給出方程的簡諧波形式的解:u=ei(kzz+kxx)eiωt---(24)]]>式中,ω為圓頻率,kx、kz分別為x、z方向的波數,單位為1/m,i為虛數單位。將上式代入波動方程有:于是有:令kz=k+iα(27)等式兩邊平方得到根據前人研究,可省去高階α2項。于是可得k和α關于黏滯彌散系數的表達式。根據Gazdag等的頻率-波數域波場延拓公式可有:P(z0+dz)=P(z0)eikzdz=P(z0)ei(k+iα)dz---(28)]]>其中,ei(k+iα)dz為相移因子,利用上式即可進行疊前黏滯-彌散波動方程正演數值模擬。根據斑塊飽和模型中地震波相速度的頻散關系(式21),將其代入上述計算波數的公式(式26-28)求得相移因子,設計模型即可對含氣砂巖的地震響應特征進行較準確的分析。附圖1為設計的三層地質模型,其中上層和底層為頁巖,中間為含氣砂巖儲層。設計一個欠壓實的砂巖,給定其滲透率、孔隙度等物性參數,其中巖石顆粒的體積模量均為38GPa,密度均為2.65g/cm3,干巖石的體積模量和剪切模量分別為1.56GPa和1.10GPa,孔隙度為33%,孔隙中所含氣的體積模量為0.03GPa,密度為0.15g/cm3,水的體積模量為2.42GPa,密度為1.0g/cm3。利用所述技術路線,首先可得到如圖2所示基于斑塊飽和模型的欠壓實砂巖儲層中地震P波相速度和逆品質因子的頻散關系曲線。從圖中可以看出,當含氣飽和度增大,介質中流體對地震波的衰減產生了巨大的影響,導致其速度發生了數百米每秒的降低,且在低頻段發生了較明顯的頻散現象。而逆品質因子的頻散曲線則表明了,含氣飽和度增大能夠使逆品質因子的峰值向高頻方向移動,峰值頻率時地震波速度衰減最強。圖2不同含氣飽和度下地震波相速度與逆品質因子的頻散關系曲線進而根據二維黏滯-彌散波動方程,代入斑塊飽和模型的速度頻散關系,并基于圖1所示的地質模型,可以得到如圖3所示的第128道疊前數值模擬結果,從圖中可以明顯地看到由于含氣量的增加,流體對地震波的衰減增強,導致儲層下界面反射出現明顯的時間延遲和振幅變化,其中振幅受儲層波阻抗變化的影響而增大。提取儲層下反射界面地震波的頻譜,如附圖4所示,可以看到地震波的主頻隨著儲層中含流體量增加逐漸向低頻移動,反映出地震波在高頻段的衰減變強。根據上述方法,基于球狀斑塊飽和模型,利用黏滯-彌散波動方程正演,能夠有效地反映經典含氣砂巖中地震波因流體的存在而發生的衰減和損失,巖石物理模型與地震波動方程正演的結合能夠提供更加準確的地震模型正演方法,這能夠為進一步理解含流體層的地震響應提供一定理論支持。最后應說明的是:以上實施例僅用以說明本發明的技術方案,而非對其限制;盡管參照前述實施例對本發明進行了詳細的說明,本領域的普通技術人員應當理解:其依然可以對前述各實施例所記載的技術方案進行修改,或者對其中部分技術特征進行等同替換;而這些修改或者替換,并不使相應技術方案的本質脫離本發明各實施例技術方案的精神和范圍。當前第1頁1 2 3
相關技術
網友詢問留言
已有0條留言
- 還沒有人留言評論。精彩留言會獲得點贊!
1