一種基于走時增量雙線性插值射線追蹤的井間地震層析反演方法與流程

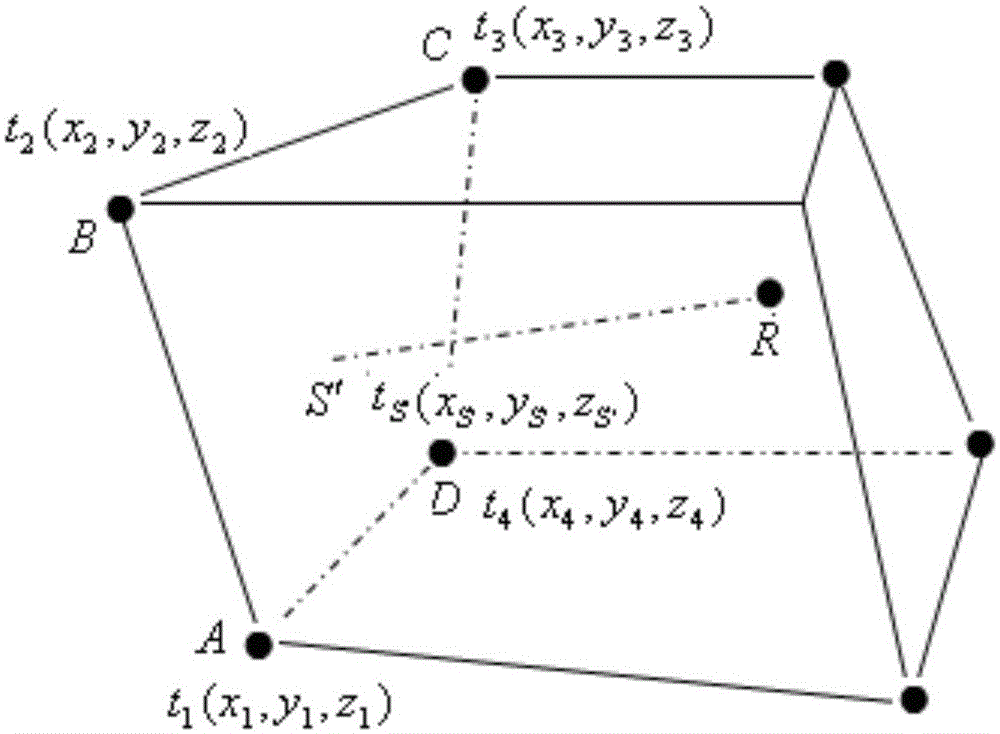
本發明屬于油氣勘探地震資料處理領域，是一種井間地震資料層析速度反演的有效方法。現有技術目前，井間地震走時層析成像應用廣泛，但分辨率和精度不高，主要是射線追蹤方法的精度和適應性嚴重地影響著旅行時層析成像的精度和可靠性。常規的射線追蹤方法主要包括試射法、彎曲法、最短路徑法和波前射線追蹤等方法。試射法在介質速度結構較復雜時，難以確定震源點到所有接收點的射線路徑。彎曲法對層狀介質模型的適應性較強，但有時會收斂到一個局部最小旅行時的路徑，而且計算成本太高。最短路徑法計算出的走時比實際走時系統偏大，射線路徑呈“之”字形，也比實際路徑長。基于程函方程的波前射線追蹤方法，效率較高，而且能夠容易追蹤到全局最小旅行時的路徑；但常常基于矩形單元模型，對層狀介質模型的適應性較差。技術實現要素：本發明的目的是針對常規射線追蹤方法存在的射線路徑和走時計算存在誤差、計算精度不高的問題，提出了一種基于走時增量雙線性插值射線追蹤的井間地震層析反演方法。本發明的一種基于走時增量雙線性插值射線追蹤的井間地震層析反演方法包括:(1)獲取井間地震資料的直達波和反射波走時；(2)建立離散初始模型；(3)計算直達波和反射波波前走時；(4)計算直達波和反射波射線路徑；(5)建立層析反演方程；(6)求解該反演方程；(7)將第(2)步的速度模型作為初始速度模型進行迭代反演，通過第(6)步解反演方程，獲取迭代后的速度模型，重復第(2)-(6)步，直到得到最終 的速度模型。上述方案進一步細化方案：(1)獲取地震資料的直達波和反射波走時；(2)建立不規則單元離散化模型，采用地層產狀先驗信息確定模型地層產狀基本架構，然后沿垂直z方向離散化模型，水平方向布置等間距的節點，采用不規則網格剖分法把初始模型離散成若干個不規則六面體單元，用網格節點處的速度值表示整個模型速度的變化；(3)計算直達波或反射波波前走時，采用基于走時增量雙線性插值的三維波前走時計算方法同時計算直達波和反射波波前走時；(4)計算直達波或反射波射線路徑，采用基于波前走時增量雙線性插值的射線追蹤方法計算射線路徑；(5)建立層析反演方程，充分考慮地層先驗信息約束，聯合直達波走時與反射波走時，并引入平滑因子穩定反演條件，建立直達波與反射走時殘差與網格節點慢度和深度修正量之間滿足的線性方程；(6)求解該反演方程，采用阻尼LSQR算法求解該反演方程，帶阻尼LSQR算法求解的是ATAx＝ATb，并能夠在求解的過程中施加一定的阻尼，當數據誤差較大時能進行有效的抑制；(7)將第(2)步的速度模型作為初始速度模型進行迭代反演，通過第(6)步解反演方程，獲取迭代后的速度模型，重復第(2)-(6)步6-10次，直到滿足收斂條件和反演效果。上述方案進一步包括：所述步驟(4)計算直達波或反射波射線路徑中，對于直達波，在計算出的不規則離散介質模型中所有網格節點上的從激發點傳播的波前傳播時間后，根據互換原理，從接收點開始，反向確定滿足Fermat原理的射線在相應單元界面上的位置，直至追蹤到源點所在單元為止，從而獲得相應的射線路徑；對于反射波，先利用上行波波前時間，從接收點開始，反向確定滿足Fermat原理的射線，直至進行到速度界面上為止，界面上的該點，即為對應的反射點；然后再利用下行波時間，從反射點開始，反向追蹤反射點到源點的射線，最后連接源點至反射點以及反射點到接收點的射線，便得到從源點到接收點的反射射線路徑；兩者的整個過程均需要不斷地在每個不規則六面體網格單元內確定射線路徑。所述步驟(4)計算直達波或反射波射線路徑中，單個不規則六面體網格單元內確定射線路徑的方法為：設接收點R在該單元內部或某個界面上，且坐標為(xR,yR,zR)，根據最小時間原理，確定該單元內的射線問題就轉化為在該單元界面上求一點S′，使波從S′到R的傳播時間達到最小；假設所求的點S′位于六面單元的左界面上，坐標記為，左界面上四個頂點A,B,C,D的坐標分別為(x1,y1,z1),(x2,y2,z2),(x3,y3,z3),(x4,y4,z4)，且它們對應的波前時間分別為t1,t2,t3,t4，假設在該左界面上，波前時間線性變化，則S′點的波前時間可由這四個頂點上波前時間的雙線性插值函數表示為：tS′＝a·Δx+b·Δy+c·Δx·Δy+d(1)波經過S′傳播到E的時間為：tE=tS′+s·(x0+Δx-xE)2+(y0+Δy-yE)2+(z0+a1Δx+b1Δy+c1-zE)2---(2)]]>其中：a1=-A0C0,b1=-B0C0,c1=-A0(x0-x1)+B0(y0-y1)C0+z1-z0;]]>而A0=(y2-y1)(z3-z1)-(y3-y1)(z2-z1)B0=(x3-x1)(z2-z1)-(x2-x1)(z3-z1)C0=(x2-x1)(y3-y1)-(x3-x1)(y2-y1);]]>(x0,y0,z0)為界面的中心點坐標，即x0＝(x1+x2)/2，y0＝(y1+y2)/2，z0＝(z1+z3)/2即可根據算式(2)計算出波經過六面體各個界面到達接收點R的傳播時間和相應的S′點位置；在這些傳播時間中選取最小值，該最小值所對應的插值邊界點S′便是射線路徑的通過點，該點與接收點的連線即為該單元內的射線路徑。在此基礎上，從源點到接收點的直達波射線追蹤步驟如下：步驟一：在接收點所在單元內，利用該單元網格節點上計算出的波前傳播時間，按照上述方法確定到達接收點的射線與該單元界面的交點，如果接收點位于單元邊界或網格節點上，這時要同時考慮接收點所在的所有單元的界面；步驟二：以該交點為新的接收點，重復步驟一,以確定第二個單元網格上的射線與單元邊界的交點，依次類推,確定射線與其穿過的所有單元界面的交點。步驟三：若追蹤到的交點位于源點所在單元內，則終止射線追蹤；否則，返回步驟二繼續追蹤。步驟四：把源點和確定的所有交點及接收點順次相連，就得到了源點到該接收點的直達波射線路徑；從源點到接收點的反射波射線追蹤分為反射路徑和入射路徑兩部分,具體步驟如下：(1)利用來自某反射面的反射波前時間，計算反射路徑部分：(1.1)在接收點所在單元內，利用該單元網格節點上計算出的反射波前傳播時間，按照上述直達波射線路徑確定方法確定到達接收點的射線與該單元界面的交點，如果接收點位于單元邊界或網格節點上，這時要同時考慮接收點所在的所有單元的界面；(1.2)若確定的交點位于反射面上，此交點即為該反射面上的反射點，即完成了反射路徑部分的射線追蹤，則可進行入射路徑的射線追蹤,其步驟按照下文中步驟(2),否則若仍未達到反射面，則按照步驟(1.3)繼續進行反射路徑的追蹤；(1.3)以該交點為新的接收點，重復步驟(1.1)，依次確定射線與其穿過的各個單元界面的交點,直到確定完反射路徑的射線與其穿過的所有單元界面的交點。(2)利用來自源點的入射波前時間，計算入射路徑：(2.1)以反射點為新的接收點，利用入射波前時間，重復步驟(1.1)；(2.2)若確定的交點位于源點所在單元內，終止射線追蹤；否則，跳到(2.3)；(2.3)以該交點為新的接收點，重復步驟(2.1)，依次確定射線與其穿過的各個單元界面的交點；(3)把源點和確定的所有交點及接收點順次相連，就得到了源點到該接 收點的反射射線路徑。所述步驟(5)建立層析反演方程中，層析反演的目標函數的表達式為：φ(s,d)=ρ1(ttrancal(s,d)-ttranobs)TCtran-1(ttrancal(s,d)-ttranobs)+ρ2(treflcal(s,d)-treflobs)TCrefl-1(treflcal(s,d)-treflobs)+λs1ΣsTLTCslow-1Ls+λd1ΣdTLTCdepth-1Ld+λs2(s-sprior)TCslow-1(s-sprior)+λd2(d-dprior)TCdepth-1(d-dprior)---(3)]]>其中，s表示模型慢度向量，d表示界面深度向量，Ctran、Crefl、Cslow、Cdepth分別表示透射波旅行時、反射波旅行時、模型速度、界面深度空間對應的先驗協方差矩陣；λs1、λd1、λs2、λd2分別為控制各項作用大小的權系數，ρ1和ρ2是取值為0和1的常系數，用于控制使用不同類型的旅行時數據；上式第一項表示透射波旅行時實測值與計算值之間的差異；第二項表示反射波旅行時實測值與計算值之間的差異；第三項和號內表示一層介質慢度的平滑程度，求和后表示所有層慢度值的光滑程度，L為光滑算子，可以采用二階差分算子，即sTLTLs=Σk=1K[(∂2s∂x2)2+(∂2s∂z2)2+2(∂2s∂x∂z)2]]]>用二階差分計算；第四項和號內表示一個界面的深度的平滑程度，求和后表示所有界面深度的光滑程度，L為光滑算子，可以采用二階差分算子，即sTLTLs=Σk=1K(∂2d∂x2)2]]>用二階差分計算；第五項表示反演出的模型慢度值與已知的模型慢度值之間的差異；第六項表示反演出的界面深度值與已知的界面深度值之間的差異；這兩項是用已知模型數據對反演結果進行約束；系數λs2或λd2是相應的權重因子。發明效果本發明的方法能夠較好地獲取兩井之間的速度模型，有著其他技術不具備的優勢，其具體優勢和特點表現在以下幾個方面：第一、技術效果的可靠性。該方法充分考慮地層先驗信息，網格剖分采用不規則六面體單元網格，使初始模型作為反演的約束條件，降低了反演的多解性，射線追蹤時采用基于走時增量的雙線性插值波前走時計算，把走時表示成背景走時與走時增量之和，假設走時增量在單元邊界上雙線性變化，消除了射線追蹤方法在近源場存在的射線路徑和走時計算誤差較大的問題，相比單獨射線方法更符合實際地震波傳播路徑，同時聯合直達波與反射波兩種有效波場走時信息，所得到的結果可靠性更強，效果明顯。第二、射線追蹤效率和反演算法效率高，群進式波前擴展走時計算方法和走時增量雙線性插值的射線追蹤方法，直達波與反射波走時同時計算，計算效率高；阻尼LSQR全局最有解反演算法反演效率高，節省大量的內存占用，穩定性強。該方法流程及參數設置簡單，運算速度快，適合應用于射線條數非常大的井間地震資料層析反演處理。附圖說明圖1一種基于走時增量雙線性插值射線追蹤的井間地震層析反演方法的處理流程圖。圖2為不規則單元內射線穿過某一界面ABCD到達某一點R的幾何關系圖。圖中A、B、C、D為單元左界面的頂點。S為射線與ABCD界面的交點，R為接收點。圖3為常規方法計算的走時誤差與本發明方法計算的走時誤差對比。圖中左側視圖為常規方法計算的走時誤差，右側為本發明方法計算的走時誤差。圖4為常規方法和本發明的基于走時增量雙線性插值波前走時計算方法計算的直達波時間與理論值的比較。圖5為起伏地層模型的層析反演效果。圖中：左側為理論模型切片；中間為用常規射線追蹤方法的層析反演切片；右側用本發明方法的層析反演切片。具體實施方式下面結合附圖1對本發明的技術方案做進一步說明。一種基于走時增量雙線性插值射線追蹤的井間地震層析反演方法，包括：(1)獲取地震資料的直達波和反射波走時。(2)建立不規則單元離散化模型。采用地層產狀先驗信息確定模型地層產狀基本架構，然后沿垂直z方向離散化模型，水平方向布置等間距的節點，采用不規則網格剖分法把初始模型離散成若干個不規則六面體單元，用網格節點處的速度值表示整個模型速度的變化。(3)計算直達波或反射波波前走時。采用基于走時增量雙線性插值的三維波前走時計算方法同時計算直達波和反射波波前走時。(4)計算直達波或反射波射線路徑。采用基于波前走時增量雙線性插值的射線追蹤方法計算射線路徑。對于直達波，在計算出的不規則離散介質模型中所有網格節點上的從激發點傳播的波前傳播時間后，根據互換原理，從接收點開始，反向確定滿足Fermat原理的射線在相應單元界面上的位置，直至追蹤到源點所在單元為止，從而獲得相應的射線路徑，提高射線追蹤精度；對于反射波，先利用上行波波前時間，從接收點開始，反向確定滿足Fermat原理的射線，直至進行到速度界面上為止，界面上的該點，即為對應的反射點；然后再利用下行波時間，從反射點開始，反向追蹤反射點到源點的射線，最后連接源點至反射點以及反射點到接收點的射線，便得到從源點到接收點的反射射線路徑。兩者的整個過程均需要不斷地在每個不規則六面體網格單元內確定射線路徑。(5)建立層析反演方程。充分考慮地層先驗信息約束，聯合直達波走時與反射波走時，并引入平滑因子穩定反演條件，建立直達波與反射走時殘差與網格節點慢度和深度修正量之間滿足的線性方程。(6)求解該反演方程。采用阻尼LSQR算法求解該反演方程，帶阻尼LSQR算法求解的是ATAx＝ATb，并能夠在求解的過程中施加一定的阻尼，當數據誤差較大時能進行有效的抑制，提高了反演的抗噪聲能力。與其他求解方法相比，可以節省較多的內存占用，同時提高計算效率。(7)將第(2)步的速度模型作為初始速度模型進行迭代反演。通過第(6)步解反演方程，獲取迭代后的速度模型，重復第(2)-(6)步6-10次，直到滿足收斂條件和反演效果。上述實施例的優化方案是：(1)獲取地震資料的直達波和反射波走時。(2)建立不規則單元離散化模型。采用地層產狀先驗信息確定模型地層產狀基本架構，然后沿垂直z方向離散化模型，水平方向布置等間距的節點，采用不規則網格剖分法把初始模型離散成若干個不規則六面體單元，用網格節點處的速度值表示整個模型速度的變化。(3)計算直達波或反射波波前走時。采用基于走時增量雙線性插值的三維波前走時計算方法同時計算直達波和反射波波前走時。先從源點開始，按照波前擴展思路采用效率非常高的GMM群快速步進方法計算波前走時至介質分界面，再從介質分界面上的最小走時節點開始向下，計算界面以下介質節點上的波前時間。(4)計算直達波或反射波射線路徑。采用基于波前走時增量雙線性插值的射線追蹤方法。對于直達波，在計算出的不規則離散介質模型中所有網格節點上的從激發點傳播的波前傳播時間后，根據互換原理，從接收點開始，反向確定滿足Fermat原理的射線在相應單元界面上的位置，直至追蹤到源點所在單元為止，從而獲得相應的透射波射線路徑，提高射線追蹤精度；對于反射波，先利用上行波波前時間，從接收點開始，反向確定滿足Fermat原理的射線，直至進行到速度界面上為止，界面上的該點，即為對應的反射點；然后，再利用下行波時間，從反射點開始，反向追蹤反射點到源點的射線，最后連接源點至反射點以及反射點到接收點的射線，便得到從源點到接收點的反射射線路徑。兩者的整個過程均需要不斷地在每個不規則六面體網格單元內確定射線路徑。其中單個不規則六面體網格單元內確定射線路徑的方法為：設接收點R在該單元內部或某個界面上，且坐標為(xR,yR,zR)，如圖2所示，根據最小時間原理，確定該單元內的射線問題就轉化為在該單元界面上求一點S′，使波從S′到R的傳播時間達到最小。假設所求的點S′位于圖2的六面單元的左界面上，坐標記為左界面上四個頂點A,B,C,D的坐標分別為(x1,y1,z1),(x2,y2,z2),(x3,y3,z3),(x4,y4,z4)，且它們對應的波前時間分別為t1,t2,t3,t4。假設在該左界面上，波前時間線性變化，則S′點的波前時間可由這四個頂點上波前時間的雙線性插值函數表示為：tS′＝a·Δx+b·Δy+c·Δx·Δy+d(1)波經過S′傳播到E的時間為：tE=tS′+s·(x0+Δx-xE)2+(y0+Δy-yE)2+(z0+a1Δx+b1Δy+c1-zE)2---(2)]]>其中：a1=-A0C0,b1=-B0C0,c1=-A0(x0-x1)+B0(y0-y1)C0+z1-z0;]]>而A0=(y2-y1)(z3-z1)-(y3-y1)(z2-z1)B0=(x3-x1)(z2-z1)-(x2-x1)(z3-z1)C0=(x2-x1)(y3-y1)-(x3-x1)(y2-y1);]]>(x0,y0,z0)為界面的中心點坐標，即x0＝(x1+x2)/2，y0＝(y1+y2)/2，z0＝(z1+z3)/2即可根據算式(2)計算出波經過六面體各個界面到達接收點R的傳播時間和相應的S′點位置。在這些傳播時間中選取最小值，該最小值所對應的插值邊界點S′便是射線路徑的通過點，該點與接收點的連線即為該單元內的射線路徑。在此基礎上，從源點到接收點的直達波射線追蹤步驟如下：步驟一：在接收點所在單元內，利用該單元網格節點上計算出的波前傳播時間，按照上述方法確定到達接收點的射線與該單元界面的交點，如果接收點位于單元邊界或網格節點上，這時要同時考慮接收點所在的所有單元的界面；步驟二：以該交點為新的接收點，重復步驟一,以確定第二個單元網格上的射線與單元邊界的交點，依次類推,確定射線與其穿過的所有單元界面的交點。步驟三：若追蹤到的交點位于源點所在單元內，則終止射線追蹤；否則，返回步驟二繼續追蹤。步驟四：把源點和確定的所有交點及接收點順次相連，就得到了源點到該接收點的直達波射線路徑；從源點到接收點的反射波射線追蹤分為反射路徑和入射路徑兩部分,具體步驟如下：(1)利用來自某反射面的反射波前時間，計算反射路徑部分：(1.1)在接收點所在單元內，利用該單元網格節點上計算出的反射波前傳播時間，按照上述直達波射線路徑確定方法確定到達接收點的射線與該單元界面的交點，如果接收點位于單元邊界或網格節點上，這時要同時考慮接收點所在的所有單元的界面；(1.2)若確定的交點位于反射面上，此交點即為該反射面上的反射點，即完成了反射路徑部分的射線追蹤，則可進行入射路徑的射線追蹤,其步驟按照下文中步驟(2),否則若仍未達到反射面，則按照步驟(1.3)繼續進行反射路徑的追蹤；(1.3)以該交點為新的接收點，重復步驟(1.1)，依次確定射線與其穿過的各個單元界面的交點,直到確定完反射路徑的射線與其穿過的所有單元界面的交點。(2)利用來自源點的入射波前時間，計算入射路徑：(2.1)以反射點為新的接收點，利用入射波前時間，重復步驟(1.1)；(2.2)若確定的交點位于源點所在單元內，終止射線追蹤；否則，跳到(2.3)；(2.3)以該交點為新的接收點，重復步驟(2.1)，依次確定射線與其穿過的各個單元界面的交點；(3)把源點和確定的所有交點及接收點順次相連，就得到了源點到該接收點的反射射線路徑。(5)建立層析反演方程，充分考慮地層先驗信息約束，聯合直達波走時與反射波走時，并引入平滑因子穩定反演條件，建立直達波與反射走時殘差與網格節點慢度和深度修正量之間滿足的線性方程；層析反演的目標函數的表達式為：φ(s,d)=ρ1(ttrancal(s,d)-ttranobs)TCtran-1(ttrancal(s,d)-ttranobs)+ρ2(treflcal(s,d)-treflobs)TCrefl-1(treflcal(s,d)-treflobs)+λs1ΣsTLTCslow-1Ls+λd1ΣdTLTCdepth-1Ld+λs2(s-sprior)TCslow-1(s-sprior)+λd2(d-dprior)TCdepth-1(d-dprior)---(3)]]>其中，s表示模型慢度向量，d表示界面深度向量，Ctran、Crefl、Cslow、Cdepth分別表示透射波旅行時、反射波旅行時、模型速度、界面深度空間對應的先驗協方差矩陣；λs1、λd1、λs2、λd2分別為控制各項作用大小的權系數。ρ1和ρ2是取值為0和1的常系數，用于控制使用不同類型的旅行時數據。上式第一項表示透射波(直達波)旅行時實測值與計算值之間的差異；第二項表示反射波旅行時實測值與計算值之間的差異；第三項和號內表示一層介質慢度的平滑程度，求和后表示所有層慢度值的光滑程度。L為光滑算子，可以采用二階差分算子，即sTLTLs=Σk=1K[(∂2s∂x2)2+(∂2s∂z2)2+2(∂2s∂x∂z)2]]]>用二階差分計算。第四項和號內表示一個界面的深度的平滑程度，求和后表示所有界面深度的光滑程度。L為光滑算子，可以采用二階差分算子，即sTLTLs=Σk=1K(∂2d∂x2)2]]>用二階差分計算。第五項表示反演出的模型慢度值與已知的模型慢度值之間的差異；第六項表 示反演出的界面深度值與已知的界面深度值之間的差異。這兩項是用已知模型數據對反演結果進行約束。系數λs2或λd2是相應的權重因子。(6)求解該反演方程，采用阻尼LSQR算法求解該反演方程，帶阻尼LSQR算法求解的是ATAx＝ATb，并能夠在求解的過程中施加一定的阻尼，當數據誤差較大時能進行有效的抑制，提高了反演的抗噪聲能力。與其他求解方法相比，可以節省較多的內存占用，同時提高計算效率；(7)將第(2)步的速度模型作為初始速度模型進行迭代反演，通過第(6)步解反演方程，獲取迭代后的速度模型，重復第(2)-(6)步6-10次，直到滿足收斂條件和反演效果，收斂條件為使迭代均方根殘差小于一個采樣點，井間地震一般為0.5ms采樣；反演效果要求為井旁層析反演的速度曲線與聲波測井曲線速度誤差小于10％，即得到最終的速度模型。本發明的實施首先對理論變速模型的走時進行了波前走時計算：圖3所示是用常規插值方法和本發明插值方法計算的波前走時與理論走時的比較。模型長度100米，厚度10米，深度方向500米，速度隨深度線性變化，在地表速度2000m/s，模型底部速度3000m/s；炮點位于左邊界25米深度上。離散單元大小10m×10m×10m。其中，左圖是常規插值方法計算的波前走時與理論走時誤差；右圖是本發明插值方法計算的波前走時與理論走時誤差；從結果可以看出，常規插值方法計算的走時誤差在近場位置達到本發明插值0.05ms以上，本發明方法的走時誤差基本在0.01ms以內，本發明的走時計算方法比常規方法計算的波前走時的誤差減小了2倍以上，特別是在近場區，原方法的誤差較大，而新方法誤差小得多。圖4所示的是不同方法計算的直達波走時比較。圖形中最上面的跳躍較多的曲線是常規方法計算的直達波時距曲線，其下為本發明方法計算的時距曲線，最下方曲線為理論走時曲線，結果表明：常規方法計算的直達波時距曲線有較大的誤差，且偏移距越小，誤差越大；而本發明方法計算的直達波走時誤差較 小，與理論值吻合得較好。試驗模型二為包含傾斜和下凹界面的起伏地層模型：井間距100m，井深960m，模型在垂直于兩井連線的方向上的厚度為10m，由五層勻速介質組成，從上至下，速度分別為2000m/s，2300m/s，2000m/s和2200m/s；4個反射界面，從上到下分別是斜界面、下凹界面、斜界面和水平界面，該模型截面如圖5左圖所示。圖5中間為使用常規射線追蹤方法的層析反演結果，圖5右側為使用本發明方法的層析反演結果。可以看出，本發明方法結果遠遠好于原方法結果。每個分層速度與理論模型基本一致，并且界面反映準確，起伏地層的層間無假速度異常體存在，反演精度高。當前第1頁1 2 3