一種行星滾柱絲杠的螺紋齒形設計方法與流程

本發明涉及一種行星滾柱絲杠的螺紋齒形設計方法，并提供一種優選的齒形，屬于精密機械傳動的
技術領域：
。
背景技術：
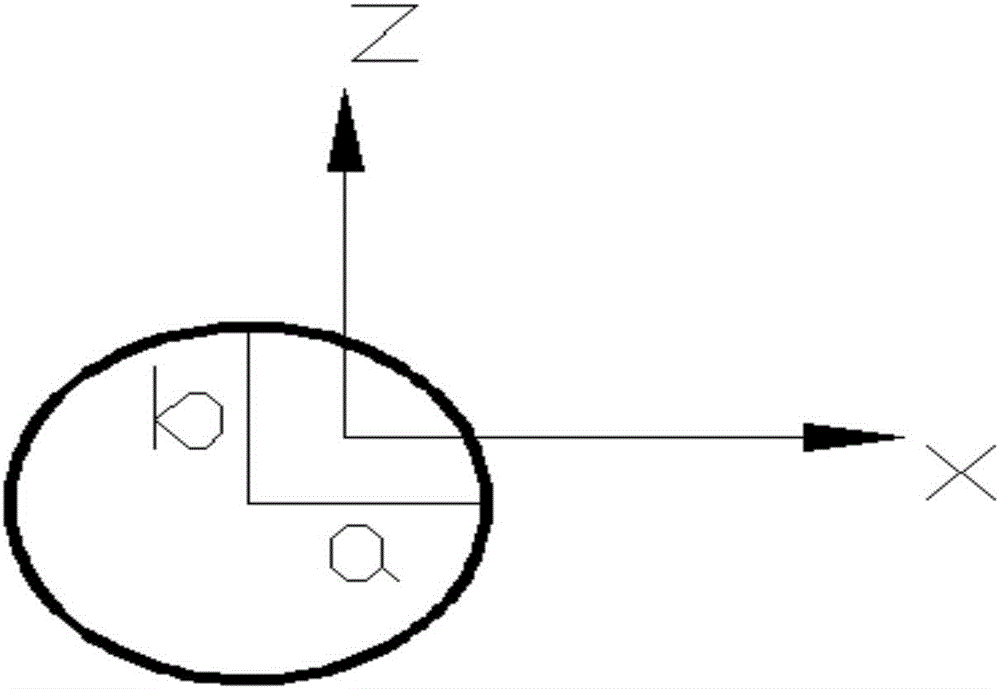
：隨著現代機械傳動機構中對于更高精度、更快速度和更高承載力等方面的要求的提高，傳統的滾珠絲杠傳動機構已經不能滿足要求，近年來出現的一種新型絲杠傳動機構——行星滾柱絲杠機構，包括外螺母、多個行星滾柱和絲杠等零件，所述多個行星滾柱絲杠均勻的布置在所述絲杠周圍，通過表面的螺紋與絲杠的螺紋形成嚙合，所述行星滾柱絲杠同時與所述螺母內螺紋形成嚙合，從而將旋轉運動轉化為直線運動。絲杠軸采用小導程角的螺紋，有利于達到小的導程和高的導程精度，可實現微量進給，目前國內很多行星滾柱絲杠的產品都是采用圓弧螺紋的行星滾柱和直線螺紋的絲杠進行配合傳動，但是此種滾柱絲杠機構，在大螺距、高傳動比的情況下容易發生邊緣嚙合，承載能力下降。技術實現要素：要解決的技術問題：為了減少圓弧形螺紋齒廓的滾柱和絲杠在嚙合過程中容易產生邊緣嚙合的問題，本專利提供一種行星滾柱絲杠的螺紋齒形設計方法，該設計方法中，滾柱的螺紋齒形為橢圓型，由于橢圓螺紋會使得滾柱和絲杠在嚙合過程中，產生的嚙合半徑最接近絲杠和滾柱的中徑，絲杠和滾柱的嚙合偏角最小，其嚙合特性要優于圓弧螺紋，其嚙合半徑大小穩定，嚙合區域集中在導程圓附近，可以避免產生邊緣嚙合。本發明專利解決其技術問題所采用的技術方案是：本發明提供一種行星滾柱絲杠的螺紋齒形設計方法,如圖14所示，其實施步驟如下：步驟一：創建坐標系，繪制滾柱橢圓輪廓齒形曲線，為方便計算，不妨將縱軸作為滾柱中心軸線，即Hcx＝0。則橢圓輪廓曲線的表達式為：其中，步驟一中所述“Hcx”為橢圓中心到x坐標軸的距離；“Hcz”為橢圓中心到z坐標軸的距離；“a和b”分別為橢圓的半長軸和半短軸。步驟二：建立直線方程y＝x與橢圓方程聯立,并且取b＝k*a,k為比例系數，且0<k<1，可得不同的k取值，對應不同的半長軸a和半短軸b：b＝k*a，其中，步驟二中所述的“r_mr”為滾柱的中徑，為給定值。步驟三：將不同的a和b的值代入MATLAB軟件進行滾柱與絲杠的嚙合點計算，嚙合方程如下：通過以上方程組可以解出5個未知數，分別是：滾柱嚙合半徑、滾柱嚙合偏角、絲杠嚙合半徑、絲杠嚙合偏角、絲杠和滾柱螺紋z方向的距離。式中，“rs_x,rs_y,rs_z”分別表示絲杠嚙合點坐標；“rr_x,rr_y,rr_z”分別表示滾柱嚙合點坐標；“ns_x,ns_y,ns_z”分別表示絲杠嚙合點法向量，“nr_x,nr_y,nr_z”分別表示滾柱嚙合點法向量；“d”表示絲杠與滾柱中心距離且d＝r_mr+r_ms；“x(5)”表示絲杠和滾柱螺紋z方向距離。其中，步驟三中所述的“MATLAB”軟件是一種用于算法開發、數據可視化、數據分析、數值計算和交互式環境的軟件；可以進行數值分析、數字圖像處理、數學模型建模、仿真和工程與科學繪圖等功能；步驟四：通過多次計算結果可以找到合適的k值，并且反復進行步驟三的嚙合點計算，使絲杠和滾柱嚙合半徑較為接近絲杠和滾柱的中心半徑，即嚙合點都在最為理想的位置。根據實驗研究和仿真計算結果，當0.8≤k≤1時，嚙合效果較好。步驟五：根據計算最優嚙合條件下的k值可以計算出a和b的值，進而計算出滾柱的牙型半角β值：x＝r_mr通過β角可以計算得出橢圓輪廓圓心的位置：進而代入橢圓輪廓直線方程可以求出行星滾柱的齒廓曲線方程。其中，步驟五中“r_mr”為給定的絲杠中徑值；p為給定的絲杠螺距值。步驟六：將所述行星滾柱按其法平面展開，即可得到其螺紋齒廓曲線為橢圓弧的螺紋分布，進而求的滾柱齒形各部分參數的含義及大小：h：所述滾柱螺紋全齒高，即滾柱螺紋齒頂到齒根之間的徑向距離，根據橢圓方程：當z＝p/2時，x＝x0；當z＝0時，x＝x1，所以全齒高h＝x1-x0；ha：所述滾柱螺紋齒頂高，即螺紋齒頂到螺紋中線之間的徑向距離，ha＝x1-r_mr；hf：所述滾柱螺紋齒根高，即螺紋齒根到螺紋中線之間的徑向距離，hf＝h-ha。步驟七：同步驟一所述，建立坐標系，繪制絲杠直線輪廓齒形曲線，表達式為：其中，步驟七中所述的“β”為直線與x軸方向夾角即絲杠螺紋牙型半角，其值為45°；步驟七中所述的“Hcz”為直線在z軸方向截距，且其中，r_ms為絲杠中徑。步驟八：消除絲杠和滾柱在嚙合過程中發生的干涉，通過仿真計算可以發現，所述絲杠和所述滾柱在嚙合過程中，非嚙合側的一側發生了嚴重的干涉，將導致正常的傳動無法進行，故需要對絲杠的螺紋齒廓進行修整。修整的方法為：由于絲杠螺紋齒為軸向對稱結構，故對一側進行修整，可以在絲杠正反向旋轉時都消除干涉，絲杠和滾柱在正確傳動時，嚙合一側發生接觸，非嚙合一側應留有間隙，即絲杠螺紋齒上的點到中心軸的距離應該小于滾柱螺紋齒上的點到中心軸的距離，根據這一原則，通過計算絲杠和滾柱非嚙合側的每一點到中心軸的距離，借助MATLAB軟件進行輔助計算，可以得出發生干涉的點，將這些干涉點取出，分別計算絲杠和滾柱所對應的干涉點在z方向的距離，通過各點距離值比較，可以計算出所述絲杠螺紋修整量x′。具體計算過程如下：(1)首先計算產生干涉的地方，產生干涉的點即滾柱上“落在”絲杠內部當中的點：式中，“x_r和y_r”分別為滾柱螺紋上各個點的x坐標和y坐標，“r_ms”為滾柱螺紋的中徑，“h”為滾柱螺紋全齒高，通過不斷的循環迭代計算，可找出滾柱上產生干涉的點的坐標集合，用x_r(i,j)和y_r(i,j)表示，軸線方向的坐標用z_r(i,j)表示；(2)將滾柱上發生干涉的點x_r(i,j)和y_r(i,j)到絲杠中心軸線的距離取出，用μ表示，即代入絲杠螺紋方程中，反解出絲杠螺紋上發生干涉的點的坐標，即:可以得到干涉區域絲杠上的點的x坐標和y坐標，式中，βs為絲杠螺紋牙型半角；(3)通過絲杠上發生干涉的點的x和y坐標，結合絲杠螺紋模型方程，可以計算出絲杠發生干涉的點在z方向上的坐標；(4)將絲杠和螺紋發生干涉的區域的點在軸向方向(z向)做差，即可得到絲杠需要向上移動的修正值，即：x′＝abs(z_s-z_r)/cos(α_s)式中，abs：代表絕對值；z_s：根據絲杠螺紋上發生干涉點的x_s(i,j)和y_s(i,j)坐標和坐標變換后的螺紋曲線方程計算的z坐標值，即z_s(i,j)；z_r：根據滾柱螺紋上發生干涉點的x_r(i,j)和y_r(i,j)坐標和坐標變換后的螺紋曲線方程計算的z坐標值，即z_r(i,j)；α_s：絲杠螺紋的螺旋升角。絲杠螺紋進行修整后，絲杠螺紋和滾柱螺紋之間的干涉將得到消除。需要注意的是，在進行干涉點的坐標計算時，應將滾柱螺紋坐標系和絲杠螺紋坐標系按照坐標系變換矩陣全部轉換到絲杠軸坐標系即固定坐標系。得到相應的絲杠和滾柱的螺紋位置方程后，再按照計算方法進行計算，即坐標系統一的原則。步驟九：所述絲杠按其法平面截開，即可得到其螺紋齒廓曲線為直線的螺紋分布，所述行星滾柱絲杠的齒形各部分參數的含義及大小為：h：所述絲杠螺紋全齒高，即絲杠螺紋齒頂到齒根之間的徑向距離，根據直線方程：當z＝p/2時，x＝x0,當z＝0時，x＝x1,所以齒高h＝x1-x0；所述絲杠螺紋在修整之前，齒頂高即螺紋齒頂到螺紋中線之間的徑向距離，齒頂高ha＝x1-r_ms；所述絲杠螺紋齒廓進行修整后，齒頂高ha會由于修整量的變化減少，最終值齒根高h′f最終值為h′f＝h-h′a。通過以上步驟，可以設計出一種滾柱螺紋曲線為橢圓的行星滾柱絲杠機構，而絲杠的螺紋曲線仍然為直線，該種齒形的滾柱螺紋嚙合特性要優于滾柱螺紋輪廓為圓弧的滾柱絲杠機構，其嚙合半徑大小穩定，嚙合區集中在導程圓附近，改善了滾柱為圓弧螺紋的行星滾柱絲杠機構易產生邊緣嚙合的缺點，從而可以提高嚙合能力，提高承載能力。有益效果：本發明提供一種行星滾柱絲杠的螺紋齒形設計方法，其特征在于：所述多個行星滾柱的螺紋輪廓曲線為橢圓弧，所述絲杠的螺紋輪廓曲線為直線。以現有行星滾柱為圓弧輪廓曲線為基礎，通過建立橢圓曲線方程，進行參數計算，之后通過MATLAB進行嚙合仿真和數值計算，再將直線齒廓螺紋進行修整，得到最終的齒形。通過該發明得到的滾柱絲杠機構，其嚙合特性要優于滾柱齒形輪廓為圓弧的滾柱絲杠機構，由于其嚙合半徑大小穩定，嚙合區集中在導程圓附近，改善了滾柱為圓弧螺紋的行星滾柱絲杠機構易產生邊緣嚙合的缺點，從而可以提高嚙合能力，提高承載能力。附圖說明圖1：橢圓曲線圖圖中a和b分別為橢圓的半長軸和半短軸；圖2：直線方程與橢圓方程聯立圖像圖中a和b分別為橢圓的半長軸和半短軸；r_mr為滾柱的中徑；(x,x)為直線方程和橢圓方程的交點坐標；圖3：β角計算示意圖圖中β角為滾柱的牙型半角；圖4：滾柱螺紋橢圓輪廓齒形中心計算示意圖圖中HCZ表示橢圓中心距離z軸的距離，p為滾柱的螺距；圖5：滾柱橢圓輪廓螺紋分布及對應尺寸參數圖中h為所述滾柱螺紋齒高；ha為所述滾柱螺紋齒頂高；hf為所述滾柱螺紋齒根高；圖6：齒高計算示意圖圖7：直線圖像圖8：絲杠螺紋直線輪廓圖像圖中r_ms為絲杠中徑；Hcz為直線在z軸方向截距；β角為絲杠的牙型半角；p為絲杠的螺距；圖9：絲杠螺紋修整前與滾柱螺紋嚙合圖圖10：絲杠螺紋修整后螺紋分布及修正參數圖中x′為絲杠螺紋修整量；圖11：絲杠螺紋修整后與滾柱螺紋嚙合圖圖12：絲杠螺紋修整后直線齒廓螺紋分布圖圖中h為所述絲杠螺紋全齒高；ha為所述絲杠螺紋齒頂高；hf為所述絲杠螺紋齒根高；圖13：絲杠齒高計算示意圖圖14：本發明所述方法流程圖具體實施方式本發明一種行星滾柱絲杠及其螺紋齒形設計方法,如圖14所示，其實施步驟如下：步驟一：創建坐標系，如圖1所示，繪制滾柱橢圓輪廓齒形曲線，為方便計算，不妨將縱軸作為滾柱中心軸線，即Hcx＝0。則橢圓輪廓曲線的表達式為：其中，步驟一中所述“Hcx”為橢圓中心到x坐標軸的距離；“Hcz”為橢圓中心到z坐標軸的距離；“a和b”分別為橢圓的半長軸和半短軸。步驟二：建立直線方程y＝x與橢圓方程聯立,如圖2所示，并且取b＝k*a,k為比例系數，且0<k<1，可得不同的k取值，對應不同的半長軸a和半短軸b，根據實驗研究和仿真計算結果，當0.8≤k≤1時，嚙合效果較好。b＝k*a，0.8≤k≤1其中，步驟二中所述的“r_mr”為滾柱的中徑，為設計過程中的條件給定值。步驟三：將不同的a和b的值代入MATLAB軟件進行滾柱與絲杠的嚙合點計算，嚙合方程如下：通過以上方程組可以解出5個未知數，分別是：滾柱嚙合半徑、滾柱嚙合偏角、絲杠嚙合半徑、絲杠嚙合偏角、絲杠和滾柱螺紋z方向的距離。其中，步驟三中所述的“MATLAB”軟件是一種用于算法開發、數據可視化。數據分析以及數值計算的高級技術計算語言和交互式環境。可以進行數值分析、數字圖像處理和工程與科學繪圖等功能；其中，步驟三所述的“rs_x,rs_y,rs_z”分別表示絲杠嚙合點坐標；“rr_x,rr_y,rr_z”分別表示滾柱嚙合點坐標；“ns_x,ns_y,ns_z”分別表示絲杠嚙合點法向量，“nr_x,nr_y,nr_z”分別表示滾柱嚙合點法向量；“d”表示絲杠與滾柱中心距離且d＝r_mr+r_ms；“x(5)”表示絲杠和滾柱螺紋z方向距離。步驟四：通過多次計算結果可以找到合適的k值，并且反復進行步驟三的嚙合點計算，使絲杠和滾柱嚙合半徑較為接近絲杠和滾柱的中心半徑，即嚙合點都在最為理想的位置。步驟五：根據計算最優嚙合條件下的k值可以計算出a和b的值，如圖3所示，可以計算出滾柱的牙型半角β值：x＝r_mr如圖4所示，通過β角可以計算得出橢圓輪廓圓心的位置：將HCZ代入橢圓輪廓直線方程可以求出行星滾柱的齒廓曲線方程。其中，步驟五中“r_mr”為給定的絲杠中徑值；p為給定的絲杠螺距值。步驟六：將所述行星滾柱按其法平面展開，即可得到其螺紋齒廓曲線為橢圓弧的螺紋分布，如圖5所示，進而可以求出滾柱齒形各部分參數的含義及大小：h：所述滾柱螺紋齒高，即滾柱螺紋齒頂到齒根之間的徑向距離，根據橢圓方程：以及圖6所示的齒高計算示意圖，可得：當z＝p/2時，x＝x0；當z＝0時，x＝x1，所以齒高h＝x1-x0；ha：所述滾柱螺紋齒頂高，即螺紋齒頂到螺紋中線之間的徑向距離，ha＝x1-r_mr；hf：所述滾柱螺紋齒根高，即螺紋齒根到螺紋中線之間的徑向距離，hf＝h-ha。步驟七：同步驟一所述，建立坐標系，繪制絲杠直線輪廓齒形曲線，如圖7所示，表達式為：其中，如圖8所示，步驟七中所述的“β”為直線與x軸方向夾角即絲杠螺紋牙型半角，其值為45°；步驟七中所述的“Hcz”為直線在z軸方向截距，且其中，r_ms為絲杠中徑。步驟八：消除絲杠和滾柱在嚙合過程中發生的干涉，根據圖9的嚙合仿真結果所示，所述絲杠和所述滾柱在嚙合過程中，非嚙合側的一側發生了嚴重的干涉，將導致正常的傳動無法進行，故需要對絲杠的螺紋齒廓進行修整。修整的方法為：由于絲杠螺紋齒為軸向對稱結構，故對一側進行修整，可以在絲杠正反向旋轉時都消除干涉，絲杠和滾柱在正確傳動時，嚙合一側發生接觸，非嚙合一側應留有間隙，即絲杠螺紋齒上的點到中心軸的距離應該小于滾柱螺紋齒上的點到中心軸的距離，根據這一原則，通過計算絲杠和滾柱非嚙合側的每一點到中心軸的距離，借助MATLAB軟件進行輔助計算，可以得出發生干涉的點，將這些干涉點取出，分別計算絲杠和滾柱所對應的干涉點在z方向的距離，通過各點距離值比較，可以計算出所述絲杠螺紋修整量x′，如圖10所示。具體計算過程如下：(1)首先計算產生干涉的地方，產生干涉的點即滾柱上“落在”絲杠內部當中的點：式中，“x_r和y_r”分別為滾柱螺紋上各個點的x坐標和y坐標，“r_ms”為滾柱螺紋的中徑，“h”為滾柱螺紋全齒高，通過不斷的循環迭代計算，可找出滾柱上產生干涉的點的坐標集合，用x_r(i,j)和y_r(i,j)表示，軸線方向的坐標用z_r(i,j)表示；(2)將滾柱上發生干涉的點x_r(i,j)和y_r(i,j)到絲杠中心軸線的距離取出，用μ表示，即代入絲杠螺紋方程中，反解出絲杠螺紋上發生干涉的點的坐標，即:可以得到干涉區域絲杠上的點的x坐標和y坐標；(3)通過絲杠上發生干涉的點的x和y坐標，結合絲杠螺紋模型方程，可以計算出絲杠發生干涉的點在z方向上的坐標；(4)將絲杠和螺紋發生干涉的區域的點在軸向方向(z向)做差，即可得到絲杠需要向上移動的修正值，即：x′＝abs(z_s-z_r)/cos(α_s)式中，abs：代表絕對值；z_s：根據絲杠螺紋上發生干涉點的x_s(i,j)和y_s(i,j)坐標和坐標變換后的螺紋曲線方程計算的z坐標值，即z_s(i,j)；z_r：根據滾柱螺紋上發生干涉點的x_r(i,j)和y_r(i,j)坐標和坐標變換后的螺紋曲線方程計算的z坐標值，即z_r(i,j)；α_s：絲杠螺紋的螺旋升角。如圖11所示的仿真結果，絲杠螺紋進行修整后，干涉將消除。需要注意的是，在進行干涉點的坐標計算時，應將滾柱螺紋坐標系和絲杠螺紋坐標系按照坐標系變換矩陣全部轉換到絲杠軸坐標系即固定坐標系。得到相應的絲杠和滾柱的螺紋位置方程后，再按照計算方法進行計算，即坐標系統一原則。步驟九：所述絲杠按其法平面截開，即可得到其螺紋齒廓曲線為直線的螺紋分布，如圖12所示，所述行星滾柱絲杠的齒形各部分參數的含義及大小為：h：所述絲杠螺紋全齒高，即絲杠螺紋齒頂到齒根之間的徑向距離，根據直線方程：以及圖13所示的齒高計算示意圖，可得：當z＝p/2時，x＝x0,當z＝0時，x＝x1,所以齒高h＝x1-x0；所述絲杠螺紋在修整之前，齒頂高即螺紋齒頂到螺紋中線之間的徑向距離，齒頂高ha＝x1-r_ms；所述絲杠螺紋齒廓進行修整后，齒頂高ha會由于修整量的變化減少，最終值齒根高h′f最終值為h′f＝h-h′a。以下，給出具體實例來說明：對于給定的滾柱中徑4.5㎜和絲杠的中徑13.5㎜，p為螺距值為2mm，牙型半角β，在圓弧螺紋滾柱和絲杠直線螺紋中其值取為45°。通過多次實驗研究表明，當k＝0.9，a＝6㎜，b＝5.4㎜，滾柱與絲杠嚙合條件最佳，計算結果如下表所示：絲杠嚙合半徑絲杠嚙合偏角滾柱嚙合半徑滾柱嚙合偏角13.5778㎜0.0460°4.5122㎜2.8892°根據計算結果可以發現，絲杠螺紋和滾柱螺紋的嚙合區域較為接近導程圓，此時，滾柱的牙型半角β值發生改變，計算方法如圖3所示，x＝r_mr＝4.5時，z＝3.57,所以通過β角可以計算得出橢圓輪廓圓心的位置，如圖4所示，即即圓心位置坐標為(0，-3)。式中，p為螺距值，根據傳動量要求所定，此處為定值2mm。因此，滾柱橢圓輪廓螺紋曲線方程為：將所述行星滾柱按其法平面截開，即可得到其螺紋齒廓曲線為橢圓弧的螺紋分布如圖5所示，所述行星滾柱絲杠的齒形各部分參數的含義及大小為：h：所述滾柱螺紋齒高，即螺紋齒頂到齒根之間的徑向距離，根據圖6所示幾何關系及橢圓方程當z＝1時，x0＝4.03mm,當z＝0時，x1＝4.98mm,所以齒高h＝x1-x0＝4.98-4.02＝0.96mm；ha：所述滾柱螺紋齒頂高，即螺紋齒頂到螺紋中線之間的徑向距離，根據圖6所示幾何關系，ha＝x1-r_mr＝4.98-4.5＝0.48mm；hf：所述滾柱螺紋齒根高，即螺紋齒根到螺紋中線之間的徑向距離，hf＝h-ha＝0.96-0.48＝0.48mm；相應的，通過絲杠β角可以算出絲杠與z軸方向截距，所以，絲杠螺紋直線齒廓方程為z＝±x+14根據圖8幾何關系及螺紋直線齒廓方程z＝±x+14，當時，x0＝13mm,當z＝0時，x1＝14mm,所以齒高h＝x1-x0＝14-13＝1mm；ha：所述滾柱螺紋齒頂高，即螺紋齒頂到螺紋中線之間的徑向距離，根據圖13幾何關系，ha＝H_cx-r_ms＝14-13.5＝0.5mm；hf：所述滾柱螺紋齒根高，即螺紋齒根到螺紋中線之間的徑向距離，hf＝h-ha＝1-0.5＝0.5mm；計算出所述絲杠螺紋修整量為0.2574㎜，實際加工過程中，可取0.26㎜，修整后所述絲杠螺紋分布見圖11所示，修整量x′＝0.26mm，細實線部分為修整前齒廓，粗實線部分為修整后齒廓。所述絲杠螺紋齒廓進行修整后，部分參數會發生變化，齒頂高ha會由于修整量的變化減少，最終值齒根高hf會由于修整量的變化增加，最終值為h′f＝h-h′a＝1-0.32＝0.68mm。修整后，所述絲杠螺紋齒廓其余參數不變，所述螺紋齒廓修整后與滾珠螺紋嚙合時，如圖11所示，干涉將會消除。當前第1頁1 2 3