一種改進的阿爾茨海默病發病風險預測方法與流程
本發明涉及醫療檢測領域,特別涉及一種改進的阿爾茨海默病發病風險預測方法。
背景技術:
阿爾茨海默病是一種神經系統退行性疾病,臨床上以記憶力減退、認知能力下降等癡呆表現為特征。現代科學認為阿爾茨海默病是基因和環境因素共同作用的結果,其中基因起著主要作用。
目前,阿爾茨海默病患者的比例逐年上升,嚴重影響著人們的日常生活。近年來,全基因組關聯研究和候選基因研究發現了大量阿爾茨海默病易感多態位點。因此,通過阿爾茨海默病個體和正常對照個體的基因型數據建立相應的模型,進而預測個體的阿爾茨海默病發病風險就顯的十分重要。
如果測定一個人的基因型數據,利用模型就可以計算出阿爾茨海默病發病風險的大小。若發病風險較高,則需要制定健康的生活、運動及營養平衡方案,從而降低發病風險。
遺傳風險評分(Genetic risk score,GRS)作為分析單核苷酸多態性(Single nucleotide polymorphisms,SNP)與復雜疾病臨床表型的有效方法。單個SNP對疾病具有微弱效應,該方法整合了若干個SNPs的微弱效應。GRS認為每個風險等位基因對疾病的作用相同,只是把風險等位基因的個數簡單相加。實際上,每個風險等位基因對疾病的作用不可能相同,于是誕生了加權的遺傳風險評分(wGRS)。
加權的GRS可以表示為:(βi表示第i個SNP的權重,Si表示第i個SNP的風險等位基因的個數,n為SNPs的數量)。該算法認為每個風險等位基因對疾病的影響不同,通過給每個風險等位基因賦予相應的權重來表明SNPs對疾病的影響程度,wGRS較GRS更廣泛應用在復雜疾病的預測評估中。
目前研究表明,SNP之間的相互作用對阿爾茨海默病發病有重要影響,而wGRS進行風險預測時忽略了SNP之間的相互作用。
技術實現要素:
本發明的目的是克服上述現有技術中存在的問題,提供一種改進的阿爾茨海默病發病風險預測方法,該方法基于阿爾茨海默病(Alzheimer disease,AD)疾病個體和正常個體的基因型數據,建立一個更準確的阿爾茨海默病風險預測模型,利用該模型及個體的基因型數據預測阿爾茨海默病的發病風險。
本發明的技術方案是:一種改進的阿爾茨海默病發病風險預測方法,包括如下步驟:
(1)獲取阿爾茨海默病疾病個體和正常對照個體的基因型數據;
對于阿爾茨海默病,首先對大量阿爾茨海默病病人和正常人的常染色體進行基因測序,得到阿爾茨海默病病人和正常人的原始SNP基因型數據;對原始的SNP基因型數據進行質量控制,剔除最小等位基因頻率MAF小于0.02、不滿足哈迪-溫伯格平衡檢驗、分型成功比小于75%、及位于連鎖不平衡區域的SNP基因型數據;樣本所對應的所有SNP的分型成功率需在75%以上,否則,再從SNP基因型數據中剔除不滿足樣本的基因型缺失比控制的樣本;對滿足條件的SNP基因型數據保留下來,用于進一步分析;
(2)剔除不滿足控制條件的SNP基因型數據后,對保留的SNP基因型數據進行評分;根據SNP基因型數據中含有的高風險等位基因的個數,對于SNP基因型數據進行0,1,2評分,采用0,1,2分來表示相應的SNP基因型數據;
對于SNP基因型數據,規定有兩個高風險等位基因的純合子記為2分,有一個高風險等位基因雜合子記為1分,有兩個低風險等位基因的純合子記為0分;
(3)與阿爾茨海默病關聯性水平p<0.05的SNP被認為是與該病顯著相關;篩選出與阿爾茨海默病顯著相關的SNP以及SNP之間的相互作用對疾病有顯著相關的SNP-SNP對;
將患阿爾茨海默病病人用1表示,正常人用0表示;通過單因素logistic回歸算法得到校正年齡、性別后與阿爾茨海默病顯著相關的SNP,同時利用Lasso多重回歸方法得到Bonferroni校正后與阿爾茨海默病顯著有關的SNP-SNP對;
(4)得到阿爾茨海默病獨立影響的SNP以及SNP之間的相互作用對疾病有獨立影響的SNP-SNP對;
比值比OR值表示疾病與暴露之間關聯強度的指標,與相對危險度(RR)類似,指暴露者的疾病危險性為非暴露者的倍數;對顯著相關的SNP和SNP對進行多因素logistic回歸算法分析,得到對阿爾茨海默病獨立影響的SNP、SNP-SNP對、相應的比值比OR值、95%置信區間以及logistic回歸的常量項α,對每一個SNP和SNP-SNP對的比值比OR值取自然對數,得到每個SNP和SNP-SNP對的權重值β;
(5)利用阿爾茨海默病獨立影響的SNP以及SNP-SNP對,建立改進的的wGRS模型;把每個SNP及SNP-SNP對都當作變量S,根據得到的每個SNP和SNP-SNP對的權重值β,于是改進的wGRS模型表示為各變量與自己的權重乘積之和,即其中n為SNP及SNP-SNP對的數量,βi表示第i個變量的權重值,Si表示第i個變量;對阿爾茨海默病獨立影響的SNP及SNP-SNP對的OR值取自然對數得到相對應的權重βi;把阿爾茨海默病獨立影響的SNP及SNP-SNP對全部納入wGRS模型,則得到阿爾茨海默病發病風險的模型為logit P(D=1|G)=α+wGRS,其中D=1表示一個人患病,G表示一個人的SNP基因數據,P(D=1|G)為一個人根據自己SNP基因數據計算出可能患阿爾茨海默病的概率,α為logistic回歸的常量項;其中n為SNP及SNP-SNP對的數量,βi表示第i個變量的權重值,Si表示第i個變量;
(6)阿爾茨海默病風險預測;
對一個人進行阿爾茨海默病風險預測,只需測定該人的基因型數據,利用步驟(5)中的阿爾茨海默病發病風險的模型就可以計算出該人患阿爾茨海默病的風險大小。
較佳地,步驟(1)中所述的對原始的SNP基因型數據進行質量控制,包括如下具體步驟:
1)對原始的SNP基因型數據,剔除最小等位基因頻率MAF小于0.02的SNP;
2)剔除不滿足哈迪-溫伯格平衡檢驗的SNP;
3)對于某個SNP在所有樣本中的分型成功率需控制在75%以上;剔除不滿足SNP分型成功比例控制的SNP;
4)對于基因組范圍內關聯分析而言,對于一個需要檢驗的樣本。一般情況下,樣本所對應的所有SNP的分型成功率需控制在75%以上,對樣本的SNP基因型數據質量控制時,從分析數據中剔除不滿足樣本的基因型缺失比控制的樣本;
5)剔除位于連鎖不平衡區域的SNP;留下的SNP基因型數據進行下一步分析。
較佳地,步驟(3)具體包括如下步驟:
(3)對SNP基因型數據進行評分完成后,將每個樣本的SNP基因型通過0,1,2表示;在進行單因素logistic回歸分析時,將單個SNP作為自變量,樣本的患病狀態0,1作為因變量,同時把年齡、性別當作協變量;則得到該SNP與阿爾茨海默病關聯性水平、比值比以及95%置信區間;若SNP與阿爾茨海默病關聯性水平p<0.05的SNP被認為是與該病顯著相關,則保留下來;
(4)利用Lasso多重回歸方法得到Bonferroni校正后與阿爾茨海默病顯著有關的SNP-SNP對。
較佳地,步驟(4)具體包括如下步驟:
1)對顯著相關的SNP和SNP-SNP對進行多因素logistic回歸算法分析時,顯著相關的SNP基因型數據通過0,1,2表示,而顯著相關的SNP-SNP對通過兩個SNP基因型數據的乘積表示,并把每個顯著相關的SNP和SNP-SNP對都看作一個變量;通過多因素logistic回歸算法,得到每個變量與阿爾茨海默病關聯性水平p值、比值比OR值、95%置信區間以及logistic回歸的常量項α;認為關聯性水平p<0.05的變量是對阿爾茨海默病獨立影響的變量;
2)對每一個SNP和SNP-SNP對的比值比OR值取自然對數,得到每個SNP和SNP-SNP對的權重值β,即每個SNP和SNP-SNP對都有對應自己的權重值β。
本發明的有益效果:本發明實施例中,提供一種改進的阿爾茨海默病發病風險預測方法,該方法基于現有的wGRS提出了改進的wGRS方法,計算wGRS時不但考慮了單個SNP的作用,同時也考慮SNP之間的相互作用。該改進的wGRS方法能夠對阿爾茨海默病發病風險預測的正確性進一步提高。因此本方法考慮到SNP之間的相互作用對阿爾茨海默病的重要影響,并將SNP之間的相互作用應用到阿爾茨海默病發病風險預測中,進一步提高了阿爾茨海默病發病風險預測的正確率。
附圖說明
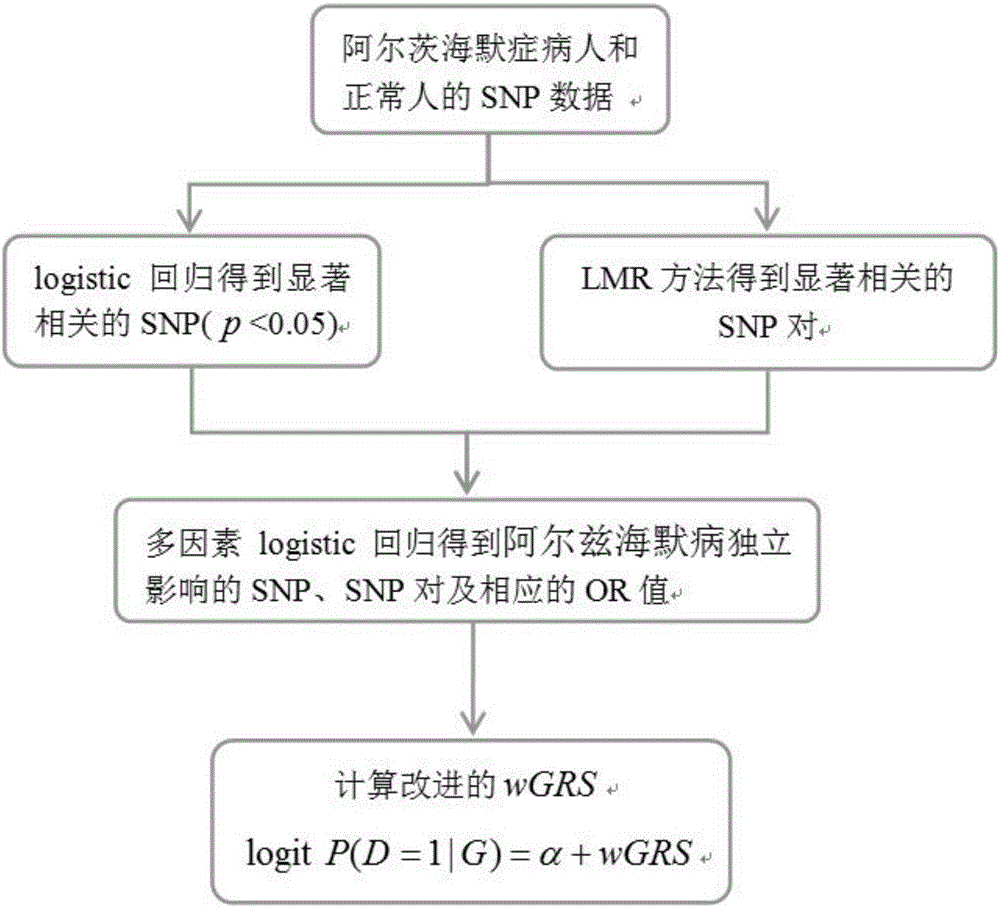
圖1為本發明的方法流程圖;
圖2為對原始樣本預測ROC曲線圖。
具體實施方式
下面結合附圖,對本發明的一個具體實施方式進行詳細描述,但應當理解本發明的保護范圍并不受具體實施方式的限制。
如圖1所示,本發明實施例提供了一種改進的阿爾茨海默病發病風險預測方法,本發明采用基因型數據預測阿爾茨海默病風險時,應用SNP之間的相互作用關系對進行阿爾茨海默病發病風險預測;本發明的目的是利用阿爾茨海默病疾病個體和正常對照個體的基因型數據訓練得到一個阿爾茨海默病風險模型,然后利用該模型及待測個體的基因型數據對阿爾茨海默病風險進行預測。本發明方法包括如下步驟:
(1)獲取阿爾茨海默病疾病個體和正常對照個體的基因型數據;
對于阿爾茨海默病,首先對大量阿爾茨海默病病人和正常人的常染色體進行基因測序,得到阿爾茨海默病病人和正常人的原始SNP基因型數據;對原始的SNP基因型數據進行質量控制,剔除最小等位基因頻率MAF小于0.02、不滿足哈迪-溫伯格平衡檢驗、分型成功比小于75%、及位于連鎖不平衡區域的SNP基因型數據;樣本所對應的所有SNP的分型成功率需在75%以上,否則,再從SNP基因型數據中剔除不滿足樣本的基因型缺失比控制的樣本;對滿足條件的SNP基因型數據保留下來,用于進一步分析;
所述的對原始的SNP基因型數據進行質量控制,包括如下具體步驟:
1)在關聯研究中,較小的MAF將會使統計效能降低,從而造成假陰性的結果。對原始的SNP基因型數據,剔除最小等位基因頻率MAF小于0.02的SNP;
2)在理想狀態下,各等位基因的頻率和等位基因的基因型頻率在遺傳中是穩定不變的,即保持著基因平衡。通常哈迪-溫伯格平衡檢驗顯著性水平p值取1×10-6。對原始的SNP基因型數據質量控制,剔除不滿足哈迪-溫伯格平衡檢驗的SNP;
3)一般情況下,對于某個SNP在所有樣本中的分型成功率需控制在75%以上,否則不能通過質量控制;剔除不滿足SNP分型成功比例控制的SNP;
4)對于基因組范圍內關聯分析而言,對于一個需要檢驗的樣本。一般情況下,樣本所對應的所有SNP的分型成功率需控制在75%以上,否則不能通過質量控制,對樣本的SNP基因型數據質量控制時,從分析數據中剔除不滿足樣本的基因型缺失比控制的樣本;
5)對原始的SNP基因型數據質量控制時,剔除位于連鎖不平衡區域的SNP;經過質量控制后,留下的SNP基因型數據進行下一步分析。
(2)剔除不滿足控制條件的SNP基因型數據后,對保留的SNP基因型數據進行評分;根據SNP基因型數據中含有的高風險等位基因的個數,對于SNP基因型數據進行0,1,2評分,采用0,1,2分來表示相應的SNP基因型數據;
對于SNP基因型數據,規定有兩個高風險等位基因的純合子記為2分,有一個高風險等位基因雜合子記為1分,有兩個低風險等位基因的純合子記為0分;
(3)與阿爾茨海默病關聯性水平p<0.05的SNP被認為是與該病顯著相關;篩選出與阿爾茨海默病顯著相關的SNP以及SNP之間的相互作用對疾病有顯著相關的SNP-SNP對;
將患阿爾茨海默病病人用1表示,正常人用0表示;通過單因素logistic回歸算法得到校正年齡、性別后與阿爾茨海默病顯著相關的SNP,同時利用Lasso多重回歸方法得到Bonferroni校正后與阿爾茨海默病顯著有關的SNP-SNP對;
本步驟(3)具體包括:
a)對SNP基因型數據進行評分完成后,將每個樣本的SNP基因型通過0,1,2表示;在進行單因素logistic回歸分析時,將單個SNP作為自變量,樣本的患病狀態0,1作為因變量,同時把年齡、性別當作協變量;則得到該SNP與阿爾茨海默病關聯性水平、比值比以及95%置信區間;若SNP與阿爾茨海默病關聯性水平p<0.05的SNP被認為是與該病顯著相關,則保留下來;
b)利用Lasso多重回歸方法得到Bonferroni校正后與阿爾茨海默病顯著有關的SNP-SNP對。
(4)得到阿爾茨海默病獨立影響的SNP以及SNP之間的相互作用對疾病有獨立影響的SNP-SNP對;
比值比OR值表示疾病與暴露之間關聯強度的指標,與相對危險度(RR)類似,指暴露者的疾病危險性為非暴露者的倍數;對顯著相關的SNP和SNP對進行多因素logistic回歸算法分析,得到對阿爾茨海默病獨立影響的SNP、SNP-SNP對、相應的比值比OR值、95%置信區間以及logistic回歸的常量項α,對每一個SNP和SNP-SNP對的比值比OR值取自然對數,得到每個SNP和SNP-SNP對的權重值β;
本步驟(4)具體包括如下步驟:
1)對顯著相關的SNP和SNP-SNP對進行多因素logistic回歸算法分析時,顯著相關的SNP基因型數據通過0,1,2表示,而顯著相關的SNP-SNP對通過兩個SNP基因型數據的乘積表示,并把每個顯著相關的SNP和SNP-SNP對都看作一個變量;通過多因素logistic回歸算法,得到每個變量與阿爾茨海默病關聯性水平p值、比值比OR值、95%置信區間以及logistic回歸的常量項α;認為關聯性水平p<0.05的變量是對阿爾茨海默病獨立影響的變量;
2)對每一個SNP和SNP-SNP對的比值比OR值取自然對數,得到每個SNP和SNP-SNP對的權重值β,即每個SNP和SNP-SNP對都有對應自己的權重值β。
(5)利用阿爾茨海默病獨立影響的SNP以及SNP-SNP對,建立改進的的wGRS模型;把每個SNP及SNP-SNP對都當作變量S,根據得到的每個SNP和SNP-SNP對的權重值β,于是改進的wGRS模型表示為各變量與自己的權重乘積之和,即其中n為SNP及SNP-SNP對的數量,βi表示第i個變量的權重值,Si表示第i個變量;對阿爾茨海默病獨立影響的SNP及SNP-SNP對的OR值取自然對數得到相對應的權重βi;把阿爾茨海默病獨立影響的SNP及SNP-SNP對全部納入wGRS模型,則得到阿爾茨海默病發病風險的模型為logit P(D=1|G)=α+wGRS,其中D=1表示一個人患病,G表示一個人的SNP基因數據,P(D=1|G)為一個人根據自己SNP基因數據計算出可能患阿爾茨海默病的概率,α為logistic回歸的常量項;其中n為SNP及SNP-SNP對的數量,βi表示第i個變量的權重值,Si表示第i個變量;
(6)阿爾茨海默病風險預測;
對一個人進行阿爾茨海默病風險預測,只需測定該人的基因型數據,利用步驟(5)中的阿爾茨海默病發病風險的模型就可以計算出該人患阿爾茨海默病的風險大小。
本發明從從如下網頁:(http://journals.plos.org/plosone/article/asset?unique&id=info:doi/10.1371/journal.pone.0144898.s002)所提供的文獻下載中國人群229阿爾茨海默病個體和318正常個體的55個阿爾茨海默病SNP的基因型數據,剔除一個不滿足的哈迪-溫伯格平衡的SNP。對所有的基因型數據按照高風險等位基因的個數進行0,1,2轉換,通過單因素logistic回歸分析可以得到與阿爾茨海默病顯著相關的SNP。由于基因型數據中沒有年齡、性別等信息,所以直接引用原作者校正年齡、性別等信息后13個與阿爾茨海默病顯著相關的SNP。詳細信息如表1所示:
表1 與AD疾病顯著相關的13個SNP
利用LMR方法找出與阿爾茨海默病顯著相關的SNP對,結果表明rs6656401-rs3865444、rs28834970-rs6656401、rs28834970-rs3865444與AD顯著相關(p<0.05)。
對13個顯著相關的SNP、3對SNP進行多因素logistic回歸,得到獨立影響阿爾茨海默病的SNP和SNP對(p<0.05)及對應的OR值和95%的置信區間(未校正年齡、性別等信息),對OR值取自然對數可以得到相應的權重β。表2是獨立影響AD的SNP和SNP對。
表2 獨立影響AD的SNP和SNP對
于是,利用獨立影響阿爾茨海默病的SNP和SNP對計算改進的wGRS,wGRS=V1*(-0.456)+V2*0.339+V3*(-0.464)+V4*0.374+V5*(-0.754)+V6*0.367+V7*0.667+V8*(-0.308)+V9*(-0.398)+V10*1.664則阿爾茨海默病疾病的模型為logit P(D=1|G)=0.772+wGRS。
為了檢驗該模型的預測正確率,我們利用改進的wGRS對原始樣本(229阿爾茨海默病個體和318正常對照個體)進行預測分析,預測結果如表3:
表3 改進的wGRS對原始樣本預測情況表(分類點為0.5)
相應的ROC曲線如圖2所示。
ROC曲線的面積為0.721,95%CI為(0.679-0.764)。
如果不考慮SNP之間的相互作用對疾病的影響,直接采用13個顯著的SNP,建立wGRS對原始樣本進行預測,得到如表4的結果分析:
表4 wGRS對原始樣本預測情況表(分類點為0.5)
因此,將阿爾茨海默病顯著相關的SNP和SNP對作為影響疾病的因素,通過多因素logistic回歸得到獨立影響阿爾茨海默病的SNP、SNP對及對應的OR值。采用改進的wGRS對阿爾茨海默病風險預測的正確率為68.7%。只用阿爾茨海默病顯著相關的SNP而不考慮SNP之間的相互作用對阿爾茨海默病風險預測的正確率為66.4%。本發明提出改進的wGRS方法充分考慮到SNP之間的相互作用對阿爾茨海默病發病的影響,能夠將阿爾茨海默病發病風險預測正確率提高2.3%。如果在進行多因素logistic回歸得到獨立影響阿爾茨海默病的SNP和SNP對時對年齡、性別等信息進行校正,相信改進的wGRS對阿爾茨海默病風險預測的正確率將會更高。
綜上所述,本發明實施例提供的一種改進的阿爾茨海默病發病風險預測方法,該方法基于現有的wGRS提出了改進的wGRS方法,計算wGRS時不但考慮了單個SNP的作用,同時也考慮SNP之間的相互作用。該改進的wGRS方法能夠對阿爾茨海默病發病風險預測的正確性進一步提高。因此本方法考慮到SNP之間的相互作用對阿爾茨海默病的重要影響,并將SNP之間的相互作用應用到阿爾茨海默病發病風險預測中,進一步提高了阿爾茨海默病發病風險預測的正確率。
以上公開的僅為本發明的幾個具體實施例,但是,本發明實施例并非局限于此,任何本領域的技術人員能思之的變化都應落入本發明的保護范圍。
- 還沒有人留言評論。精彩留言會獲得點贊!