一種直角切削顫振解析建模方法與流程
本發明涉及金屬材料切削加工技術領域,尤其涉及一種直角切削顫振解析建模方法。
背景技術:
切削顫振是由于切削力的變化以及加工系統的柔性而產生的切屑再生現象,屬于自激振動的一種形式。當不加以控制時,其會對加工工件表面質量,材料去除率,表面尺寸精度,以及刀具與機床的壽命產生破壞性影響。因此,建立有效的顫振模型是預測與避免切削顫振發生的有效措施。
迄今為止,已經形成了很多加工顫振模型,其采用的方法主要有三種:解析法、數值法及實驗法,其中切削力系數通常是通過實驗方法確定的常數。很明顯,對于給定范圍的切削參數,獲得可靠的實驗數據是非常耗時的。此外,切削力系數在實際切削過程中是變化的,經驗常數的假設將產生不準確的結果。除此之外,這些模型在缺乏切削參數(工件材料特性、刀具幾何)對切削顫振影響的直觀描述,且仍依賴于經驗或實驗的方法。
針對現有技術方案提出的建模方法的技術問題,本發明提出了一種直角切削顫振的解析建模方法,該方法從金屬切削的機理入手,將工件材料特性、刀具幾何及切削參數作為輸入參數,通過對切削參數的等效變換將動態切削過程看作是在每一時刻的準靜態切削過程,動態切削力系數可通過等效變換來解析標定,避免了實驗標定的繁瑣性。
技術實現要素:
針對上述現有技術的現狀,本發明所要解決的技術問題在于提供一種直角切削顫振解析建模方法,該方法可以克服切削力系數由實驗標定的準確度太低太繁瑣的問題,避免了實驗標定的繁瑣性,提高了切削力系數的準確度,提供一個比較真實的切削顫振穩定性的預測。
本發明解決上述技術問題所采用的技術方案為:一種直角切削顫振解析建模方法,包括以下步驟:
步驟1,建立直角切削顫振的動態模型
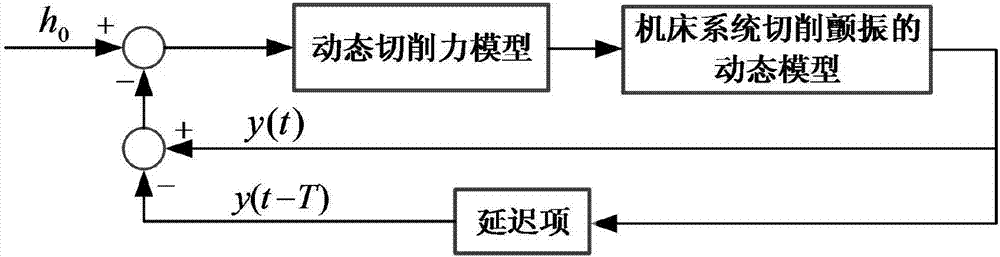
確定刀具幾何參數:前角α,單位為deg,后角γ,單位為deg;選定切削參數,切削速度v,單位為m/min,進給量ft,單位為mm/r、切削寬度b,單位為mm;在金屬切削過程中,切削厚度的變化會導致切削力的波動,切削力和切削厚度是按照特定的周期發生變化的,并形成一個閉環反饋系統,通過公式(1)計算出動態切削厚度h(t);
h(t)=h0-[y(t)-y(t-t)](1)
其中,h0為名義切削厚度,單位為mm,數值上等于刀具的進給量ft;y(t)和y(t-t)分別表示y方向的當前和前一周期的振動幅值,單位為mm,也稱為內調制和外調制,[y(t)-y(t-t)]表示在t時刻由于刀具振動產生的切削厚度差,t為當前時刻與前一時刻的延遲,即主軸旋轉周期;
在工件被認為是剛性的而刀具是柔性的情況下,機床系統切削顫振的動態模型為在進給方向的單自由度系統,進給方向即y方向,該系統的振動方程由公式(2)表示;
其中,m表示系統的等效質量,單位為kg,c表示系統的阻尼,單位為ns/m,k表示系統的等效剛度,單位為n/m,fy(t)為在進給方向由動態切削厚度h(t)引起的動態切削力;
步驟2,計算動態切削力和切削力系數
動態切削力由公式(3)表示;
fx(t)=kx(t)bh(t),fy(t)=ky(t)bh(t)(3)
其中,kx(t),ky(t)分別表示x,y方向的動態切削力系數,表示為名義切削速度v與刀具振動速度
其中,cxi,cyi,i=0,1,2是名義切削速度v的函數,通過給定范圍內的切削參數幾何標定;
將切屑的形成過程看作一個準靜態的過程,其切削波紋面的斜率ξ即為準靜態方向與有效瞬時切削方向之間的方位角,準靜態方向為x方向,有效瞬時切削方向為x′方向,斜率ξ由公式(6)表示;
其中,v為名義切削速度,單位為m/min,
然后,t時刻的有效前角α′,單位為deg,有效后角γ′,單位為deg,,有效切削厚度h′(t),單位為mm,通過準靜態切削和動態切削之間的變化關系得到,由公式(7)和公式(8)表示;
α′=α-ξ,γ′=γ+ξ(7)
其中,名義前角α和名義后角γ分別對應于準靜態切削過程的前角和后角,單位為deg;
瞬時剪切角φ′、有效切削速度v′與有效切屑速度v′c分別由公式(9)和公式(10)計算;
其中,
其中,
通過以上公式的換算,得到瞬時剪切角φ′的最終表達公式(12);
其中,a1,a2為材料特性參數,無量綱單位,瞬時剪切角φ′依賴于名義切削速度v和刀具振動速度
有效平均流動剪切應力
在每一時刻的準靜態,計算出切削波紋面的斜率ξ、有效前角α′、有效后角γ′和有效切削厚度h′(t)、有效切削速度v′、有效切屑速度v′c、瞬時剪切角φ′,進而通過代數方程整理,得出x、y方向的動態切削力系數kx(t),ky(t);
步驟3,計算直角切削過程的穩定性sld圖
首先,結合公式(2)和公式(5),并在平衡位置處引入微小振動量u(t),得到機床系統切削顫振的動態模型整理后的表達公式(15);
然后通過在公式(15)所示的平衡位置處引入微小振動量
令
其中,
通過數值求解公式(17),將時間周期t離散為n個等分小區間,即t=nτ,在每一個區間[iτ,(i+1)τ](i=0,...,n-1)的中間矩陣φ通過使用連續的離散映射di,構造公式(18)如下;
yn=φy0=dn-1dn-2…d1d0y0(18)
其中,di為離散映射矩陣,yi為2(n+1)列向量;
然后根據floquet理論,即具有周期系數的線性常微分方程,通過約化成為一個常系數的常微分方程,判別顫振系統的穩定性,當矩陣φ的所有特征值的模量小于單位1,則系統是穩定的,否則是不穩定的,進而計算出切削速度與切削寬度的關系圖,即為切削顫振系統的穩定性sld圖。
與現有技術相比,本發明的優點在于:本發明將動態切削過程看作是在每一時刻的準靜態切削過程,將工件材料特性、刀具幾何、切削參數作為輸入參數,其中動態切削力可通過等效變換的切削參數計算,進而理論推導出動態切削力系數的表達式,通過代數方程整理,得出動態切削力系數,避免了實驗標定的繁瑣性,并提高了準確度,另外,機床系統切削顫振的動態模型可以用時滯微分方程表達,通過進行切削穩定性分析,由時域半離散法獲得直角切削顫振穩定性sld圖,提供一個比較真實的顫振穩定性預測。
附圖說明
圖1是本發明實施例中直角切削顫振模型示意圖;
圖2是本發明實施例中直角切削顫振原理圖;
圖3是本發明實施例中等效參數變換圖;
圖4是本發明實施例中直角顫振sld對比圖。
具體實施方式
下面結合附圖并通過實施例對本發明作進一步的詳細說明,以下實施例是對本發明的解釋而本發明并不局限于以下實施例。
如圖1~3所示,一種直角切削顫振解析建模方法,包括以下步驟:
步驟1,建立直角切削顫振的動態模型
確定刀具幾何參數,前角α,單位為deg,后角γ,單位為deg;選定切削參數,切削速度v,單位為m/min,進給量ft,單位為mm/r、切削寬度b,單位為mm;在金屬切削過程中,切削厚度的變化會導致切削力的波動,切削力和切削厚度是按照特定的周期發生變化的,并形成一個閉環反饋系統,通過公式(1)計算出動態切削厚度h(t);
h(t)=h0-[y(t)-y(t-t)](1)
其中,h0為名義切削厚度,單位為mm,數值上等于刀具的進給量ft;y(t)和y(t-t)分別表示y方向的當前和前一周期的振動幅值,單位為mm,也稱為內調制和外調制,[y(t)-y(t-t)]表示在t時刻由于刀具振動產生的切削厚度差,t為當前時刻與前一時刻的延遲,即主軸旋轉周期;
在工件被認為是剛性的而刀具是柔性的情況下,機床系統切削顫振的動態模型為在進給方向的單自由度系統,進給方向即y方向,該系統的振動方程由公式(2)表示;
其中,m表示系統的等效質量,單位為kg,c表示系統的阻尼,單位為ns/m,k表示系統的等效剛度,單位為n/m,fy(t)為在進給方向由動態切削厚度h(t)引起的動態切削力;
步驟2,計算動態切削力和切削力系數
動態切削力由公式(3)表示;
fx(t)=kx(t)bh(t),fy(t)=ky(t)bh(t)(3)
其中,kx(t),ky(t)分別表示x,y方向的動態切削力系數,表示為名義切削速度v與刀具振動速度
其中,o表示高階無窮小,cxi,cyi,i=0,1,2是名義切削速度v的函數,通過給定范圍內的切削參數幾何標定;
將切屑的形成過程看作一個準靜態的過程,其切削波紋面的斜率ξ即為準靜態方向與有效瞬時切削方向之間的方位角,準靜態方向為x方向,有效瞬時切削方向為x′方向,斜率ξ由公式(6)表示;
其中,v為名義切削速度,單位為m/min,
然后,t時刻的有效前角α′,單位為deg,有效后角γ′,單位為deg,,有效切削厚度h′(t),單位為mm,通過準靜態切削和動態切削之間的變化關系得到,由公式(7)和公式(8)表示;
α′=α-ξ,γ′=γ+ξ(7)
其中,名義前角α和名義后角γ分別對應于準靜態切削過程的前角和后角,單位為deg;
瞬時剪切角φ′、有效切削速度v′與有效切屑速度v′c分別由公式(9)和公式(10)計算;
其中,
其中,
通過以上公式的換算,得到瞬時剪切角φ′的最終表達公式(12);
其中,a1,a2為材料特性參數,無量綱單位,瞬時剪切角φ′依賴于名義切削速度v和刀具振動速度
有效平均流動剪切應力
在每一時刻的準靜態,計算出切削波紋面的斜率ξ、有效前角α′、有效后角γ′和有效切削厚度h′(t)、有效切削速度v′、有效切屑速度v′c、瞬時剪切角φ′,進而通過代數方程整理,得出x、y方向的動態切削力系數kx(t),ky(t);
步驟3,計算直角切削過程的穩定性sld圖
首先,結合公式(2)和公式(5),并在平衡位置處引入微小振動量u(t),得到機床系統切削顫振的動態模型整理后的表達公式(15);
然后通過在公式(15)所示的平衡位置處引入微小振動量
令
其中,
通過數值求解公式(17),將時間周期t離散為n個等分小區間,即t=nτ,在每一個區間[iτ,(i+1)τ](i=0,...,n-1)的中間矩陣φ通過使用連續的離散映射di,構造公式(18)如下;
yn=φy0=dn-1dn-2…d1d0y0(18)
其中,di為離散映射矩陣,yi為2(n+1)列向量;
然后根據floquet理論,即具有周期系數的線性常微分方程,通過約化成為一個常系數的常微分方程,判別顫振系統的穩定性,當矩陣φ的所有特征值的模量小于單位1,則系統是穩定的,否則是不穩定的,進而計算出切削速度與切削寬度的關系圖,即為切削顫振系統的穩定性sld圖。
下面結合一個具體實施例來更為清晰地解釋本發明的解析建模過程。
工件材料的流動剪切應力由johnson-cook本構模型計算,直角切削過程中的機床系統切削顫振的動態模型為在進給方向的單自由度系統,另外,每一次切削過程都采用新刀片,本實施例選用的參數如表1所示:
表1解析模型所采用的參數
如圖4所示,根據表1給出的同一參數數據,由提出的解析模型與傳統顫振模型分別計算出顫振sld圖,可以看到,這兩個模型計算的結果在高切削速度區具有很好的一致性,而在低切削速度區具有很大的偏差,然而,傳統顫振模型在切削速度區與實驗結果和有限元仿真結果不一致,而本發明提出的解析模型的這種低速高穩定性現象是由于動態切削力引入了部分過程阻尼,導致了顫振穩定性的增加,因此,本發明提出的解析模型很顯然地反映這種低速穩定性現象,提供一個比較真實的顫振穩定性預測,能夠精確地預測加工過程的穩定性,解決了傳統顫振模型不能直觀解釋實際切削過程中的熱力特性以及切削力系數由實驗標定的準確度太低的問題。
顯然,本領域的技術人員可以對本發明進行各種改動和變型而不脫離本發明的精神和范圍,倘若本發明的這些修改和變型屬于本發明權利要求及其等同技術的范圍之內,則本發明包含這些改動和變型在內,本說明書中未作詳細描述的內容屬于本領域專業技術人員公知的現有技術。
- 還沒有人留言評論。精彩留言會獲得點贊!