一種厚板粗軋階段軋制力預報方法與流程
本發明涉及厚板制造技術領域,特別是涉及一種厚板粗軋階段軋制力預報方法。
背景技術:
厚板制造是國家鋼鐵裝備水平的標志,也是國家工業化水平的體現。厚板作為不可缺少的鋼材品種,廣泛用于輸油管道、鍋爐板、橋梁板、海洋平臺等構件的制造。近年來,為滿足國家國防與經濟發展需要,厚板的規格不斷增大,性能要求也不斷提高,對軋機的能力要求越來越高。為保證軋機能夠順利軋出高質量的產品,需要預先校核軋機強度并優化工藝參數,而提供準確的軋制壓力模型是完成上述要求不可缺少的依據。
小林史郎和加藤和典均對厚板的三維軋制過程進行了研究,但礙于變形區界面和自由表面二次方程的復雜性以及Mises屈服準則的非線性而只獲得了數值解。因為數值結果難以在線快速計算,致使已有技術難以取得工業應用。因此,針對厚板變形特點,提出運動許可速度場,利用線性屈服準則求解軋制能率泛函,并最終給出軋制力預測模型具有重要的工程應用價值。
因此,針對上述技術問題,有必要提供一種厚板粗軋階段軋制力預報方法。
技術實現要素:
有鑒于此,本發明的目的在于提供一種厚板粗軋階段軋制力預報方法,以預報厚板粗軋階段軋制力。
為了實現上述目的,本發明實施例提供的技術方案如下:
一種厚板粗軋階段軋制力預報方法,所述方法包括:
S1、在π平面上的誤差三角形中,通過Mises準則屈服半徑與Tresca軌跡邊心距構建一個邊心距線性組合屈服準則;
S2、根據流動法則計算材料屈服時的比塑性功率;
S3、用整體加權平均法確定厚板軋制速度場;
S4、利用比塑性功率和軋制速度場求解內部變形功率、摩擦功率、剪切功率以及總功率;
S5、基于軋制總功率極值構建厚板粗軋階段軋制力預測模型,并根據軋制力預測模型預報厚板粗軋階段軋制力。
作為本發明的進一步改進,所述步驟S1中的邊心距線性組合屈服準則為:
其中,σ1、σ2、σ3分別為主應力分量,σs為材料的屈服強度。
作為本發明的進一步改進,所述步驟S2中的比塑性功率為:
作為本發明的進一步改進,所述步驟S3中的軋制速度場表達式為:
作為本發明的進一步改進,所述步驟S4中內部變形功率摩擦功率剪切功率以及總功率分別為:
作為本發明的進一步改進,所述步驟S5中的軋制力預測模型為其中M為軋制力矩;軋制力矩Φmin為泛函最小值;應力狀態系數
本發明的有益效果是:
本發明根據線性屈服準則及比塑性功率構建的軋制力預測模型,能夠準確預報厚板粗軋階段軋制力,并能定量指導軋機的強度校核與工藝參數的優化,確保穩定軋出厚板產品。
附圖說明
為了更清楚地說明本發明實施例或現有技術中的技術方案,下面將對實施例或現有技術描述中所需要使用的附圖作簡單地介紹,顯而易見地,下面描述中的附圖僅僅是本發明中記載的一些實施例,對于本領域普通技術人員來講,在不付出創造性勞動的前提下,還可以根據這些附圖獲得其他的附圖。
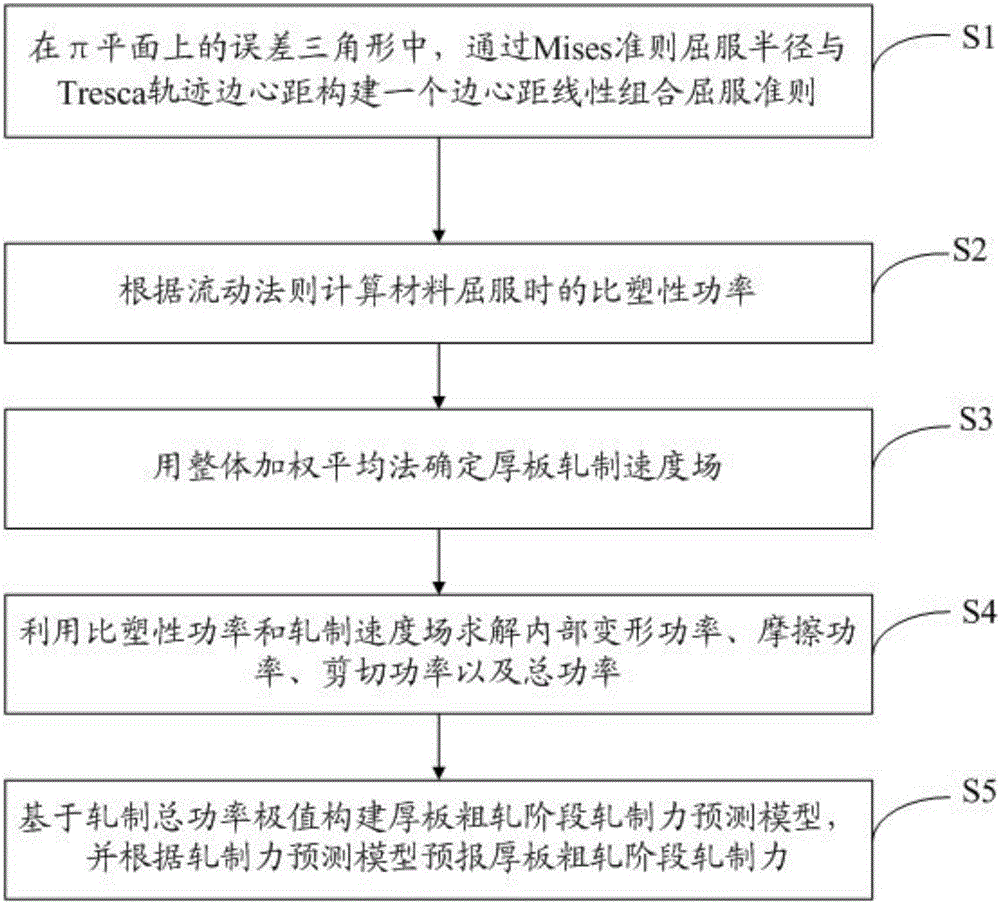
圖1為本發明厚板粗軋階段軋制力預報方法的流程圖;
圖2為本發明一具體實施方式中π平面上的屈服軌跡幾何示意圖;
圖3為本發明一具體實施方式中誤差三角形的屈服軌跡示意圖;
圖4為本發明一具體實施方式中平面上主應力分量σ1的投影示意圖;
圖5為本發明一具體實施方式中板材軋制變形區的示意圖;
圖6為本發明一具體實施方式中變形區半寬示意圖;
圖7為本發明一具體實施方式中接觸面上共線矢量τf與Δvf示意圖。
具體實施方式
為了使本技術領域的人員更好地理解本發明中的技術方案,下面將結合本發明實施例中的附圖,對本發明實施例中的技術方案進行清楚、完整地描述,顯然,所描述的實施例僅僅是本發明一部分實施例,而不是全部的實施例。基于本發明中的實施例,本領域普通技術人員在沒有做出創造性勞動前提下所獲得的所有其他實施例,都應當屬于本發明保護的范圍。
參圖1所示,本發明公開了一種厚板粗軋階段軋制力預報方法,該方法包括:
S1、在π平面上的誤差三角形中,通過Mises準則屈服半徑與Tresca軌跡邊心距構建一個邊心距線性組合屈服準則;
S2、根據流動法則計算材料屈服時的比塑性功率;
S3、用整體加權平均法確定厚板軋制速度場;
S4、利用比塑性功率和軋制速度場求解內部變形功率、摩擦功率、剪切功率以及總功率;
S5、基于軋制總功率極值構建厚板粗軋階段軋制力預測模型,并根據軋制力預測模型預報厚板粗軋階段軋制力。
以下對本發明中厚板粗軋階段軋制力預報方法的各步驟進行詳細說明。
(1)屈服準則線性化
1.1屈服假定
如圖2和3所示,Tresca準則的偏差矢量模長沿著B′F從OB′變為OF,Mises準則的偏差矢量模長沿著從OB′變為OD,TSS準則的偏差矢量模長沿著B′B從OB′變為OB。直線OF是Tresca軌跡的邊心距,OB′是TSS軌跡的邊心距。直線OI為OF與OB′的幾何平均值,在此處定義成邊心距線性組合(ALC)屈服準則。垂直于OI線的B′E是新屈服準則軌跡的十二分之一。
根據上述屈服假定,并考慮到Mises準則的屈服半徑為Tresca軌跡的邊心距則新邊心距OI為:
在直角三角形ΔB′OI中,根據勾股定理有:
令α=∠FB′E,則有:
由兩角和正切公式,可得
tanα=0.149974 (4)
在三角形ΔB′FE,EF長度可以按下式計算:
于是,
1.2函數表達式
Haigh Westergaard空間的主應力σ1向π平面投影所形成的幾何關系如圖4所示。
根據圖3、4中的幾何關系,可得E點的應力狀態如下:
假設軌跡A′E為一直線,且滿足下式:
σ1-a1σ2-a2σ3=σs (8)
注意到屈服時有a1+a2=1,那么將式(7)中的應力分量代至式(8)中可得:
a1=0.159;a2=0.841. (9)
將所得系數回代入式(8)可得:
同理,軌跡B′E滿足的方程為:
式(10)和(11)為邊心距線性組合屈服準則的數學表達式。
1.3比塑性功率
材料屈服時,應變速率張量與應力張量滿足假定有任意正數λ≥0,μ≥0,則由式(10)和(11)可得:
以上兩式進行線性組合可得:
取則有:
注意到則有:
在頂點E處,σ2=(σ1+σ3)/2,于是式(10a)或(10b)變為:
由式(16)和式(17)可得比塑性功率為:
式中,和分別為最大與最小應變速率。
(2)三維厚板軋制力學解析
2.1軋制變形描述
由于變形區對稱僅研究變形區的1/4。坐標原點取在入口截面中點,如圖5和圖6所示,入口板坯厚度2h0,寬度2b0;軋后出口厚度減小到2h1,寬度增加到2b1。接觸弧水平投影長度為l,軋輥半徑為R。令x、y、z方向為軋件長、寬、高方向,bx,hx分別是軋件變形區內任意水平位置處的半寬和半厚度,bm,hm分別為變形區內軋件半寬、半厚的均值。接觸弧方程、參數方程及一階導數方程分別為:
2.2變形速度場
假定:軋制時軋件橫斷面保持平面,垂直線保持直線,對此先建立I、II(I為只延伸無寬展;II為只寬展無延伸)兩種簡單情況的速度場,然后用整體加權平均法確定該軋制情況的速度場。
第I種情況速度場設定為:
vyI=0,
第II種情況速度場設定為:
vxII=v0,
將式(21)與(22)中的速度分量在三個方向上同時加權,設加權系數為a,加權后的速度場為:
按幾何方程,按式(23)確定的應變速率分量為:
將上述應變速率場代入體積不變條件得a′=0。將a′=0代入式(24)得:
注意到方程(23)中,x=0時,hx=h0,vx=v0;y=0,vy=0;z=0,vz=0;且式(25)滿足故所設定的速度場滿足運動許可條件。
由a′=0知a必為常數,即式(23)和(25)與a′無關。注意到軋件橫斷面保持平面和垂直線保持直線的假定,只延伸軋制時a=1,Δb/b1=0,b0/b1=1;有寬展時a<1,Δb>0,b0/b1<1。注意到a變化在b0/b1與b1/b1(b1>b0)之間,故a可按下式計算:
2.3內部變形功率
注意到式(25)中代入ALC屈服準則比塑性功率(18)式,再對變形區積分得:
式中,U=v0h0b0=vxhxbx=vnhnbn=v1h1b1為秒流量。
2.4摩擦功率
接觸面上切向速度不連續量為:
沿接觸面切向摩擦剪應力τf=mk與切向速度不連續量Δvf為共線矢量,如圖7,采用共線矢量內積,摩擦功率為:
式中cosα,cosβ,cosγ為Δvf或τf與坐標軸夾角的余弦。由于Δvf沿輥面切向,故方向余弦由輥面切向方程確定。注意到輥面方程為則方向余弦與面積微元分別為:
注意到式(26),將式(23)代入式(28)可得速度不連續量各分量為:
將式(30)、(31)及(32)代入式(29)并注意到dz/dy=0,然后積分可得:
其中,
將I1,I2積分結果代入方程(33)并整理得
2.5剪切功率
由式(19)和(23)可知,在變形區出口橫截面上有:
x=l,h'x=0,vz|x=l=Δvz|x=l=vy|x=l=Δvy|x=l=0
故出口截面不消耗剪切功率;但在入口橫截面,由式(23)并應用積分中值定理可得
于是,消耗的剪切功率為:
2.6總功率及其最小化
將式(27)、(34)、(35)代入式總功率泛函中得:
定義壓下率ε=ln(h0/h1),同時將式(36)中的Φ對αn求導并令有:
由方程(27)、(34)、(35)得:
式中,
將式(38)代入式(37)得:
將(37)確定的αn代入(36)得泛函最小值Φmin。于是,軋制力矩、軋制力及應力狀態系數為:
其中,軋制總功率泛函表達式(36)是進行軋制力計算的依據,以下結合具體實施例進行說明。
國內某廠4300mm軋機軋制120mm厚成品板,工作輥直徑1070mm;連鑄坯尺寸為320mm×2050mm×3250mm,首道次整形軋制后軋件厚度為299mm,然后板坯轉90°進行橫軋。粗軋道次No.2—No.6壓下量較大,需要采用本申請的預測模型對軋機進行強度校核。在預測模型中,變形抗力可采用下式計算:
式中,應變速率
以第二道次為例,將該道次的軋制溫度(出、入口平均溫度)963.74℃、應變0.096、應變速率0.0628(單位1/s)代入式(41)確定出變形抗力值73.60MPa;再根據式(39)和式(36)確定出最小軋制功率泛函為18.00kW;最后根據壓下率確定出該道次力臂系數χ=0.52,經式(40)確定出預測軋制力為44707kN。
求出的預測軋制力小于該軋機的最大允許軋制力90000kN,因此該道次工藝參數制定合理,能夠保證軋機安全運行不跳閘。
其他道次計算參照第二道次進行,力臂系數χ分別取0.54,0.55,0.55,0.53。粗軋階段2-6道次的計算結果與實驗數據對比情況如表1所示。
表1預測軋制力、力矩與實驗數據對比
由表1可知,無論軋制力矩還是軋制力,其計算值均高于實測值。不過,軋制力誤差不超過6.96%,力矩最大誤差不超過14.49%,該軋制模型具有較高的預測精度,可以指導粗軋階段厚板軋制階段軋制力和軋制力矩的預報,從而為軋機設備校核與工藝參數優化提供指導。
由上述技術方案可以看出,本發明根據線性屈服準則及比塑性功率構建的軋制力預測模型,能夠預報厚板粗軋階段軋制力,并能定量指導軋機的強度校核與工藝參數的優化,確保穩定軋出厚板產品。
對于本領域技術人員而言,顯然本發明不限于上述示范性實施例的細節,而且在不背離本發明的精神或基本特征的情況下,能夠以其他的具體形式實現本發明。因此,無論從哪一點來看,均應將實施例看作是示范性的,而且是非限制性的,本發明的范圍由所附權利要求而不是上述說明限定,因此旨在將落在權利要求的等同要件的含義和范圍內的所有變化囊括在本發明內。不應將權利要求中的任何附圖標記視為限制所涉及的權利要求。
此外,應當理解,雖然本說明書按照實施方式加以描述,但并非每個實施方式僅包含一個獨立的技術方案,說明書的這種敘述方式僅僅是為清楚起見,本領域技術人員應當將說明書作為一個整體,各實施例中的技術方案也可以經適當組合,形成本領域技術人員可以理解的其他實施方式。
- 還沒有人留言評論。精彩留言會獲得點贊!