一種基于模式的同步無波前自適應光學系統的制作方法
本發明為一種無波前的自適應光學系統,特別涉及一種基于通用模式的適用于動態波前校正的同步迭代機制的自適應光學系統,適用于光通信、顯微鏡、激光光束凈化、人眼成像等應用中的波前像差校正。
背景技術:
自適應光學(Adaptive Optics,AO)是上世紀八十年代發展起來的技術。自適應光學系統根據有無專用的波前探測器分為有波前傳感的自適應光學系統和無波前傳感的自適應光學系統;其中無波前傳感的自適應光學系統(WFSless AO)廣泛應用于波前相位不連續及一些特殊應用場合如激光核聚變裝置、共焦顯微鏡、光纖耦合、激光相控、光學鉗、光學追蹤、擴展目標成像等。無波前傳感自適應光學系統在物理實驗和實際應用中能否取得良好的校正效果取決于系統采用的控制算法。
現有無波前傳感的自適應光學系統控制算法主要采用迭代尋優的方法完成波前像差校正。根據尋優空間輸出量產生方式可以分為兩類,一類方法的輸出量及施加校正單元(變形鏡)的擾動量隨機盲生成,然后向著最優化指標量方向迭代,如隨機并行梯度下降(SPGD)算法(參見Vorontsov,M.A.and Sivokon,V.P.,Stochastic parallel gradient descent technique for high-resolution wave front phase-distortion correction,Opt.Soc.Am.A.15,2745-2758,1998)。這類算法實現簡單但其收斂速度慢,尤其在像差變大、校正單元數目增多即像差校正模式數增加時,其控制量搜索空間增大,系統收斂速度急劇變慢,甚至陷入局部優化。另一類方法的控制量是一種由波前像差相關的物理量與焦平面光強分布的某種關系推導出的近似解,因此算法收斂速度快,波前校正效果好(參見M.J.Booth,Wavefront sensorless adaptive optics for large aberrations,Opt.Lett.32,5–7,2007.)。針對這類算法對波前像差大小情況采用不同控制算法帶來的問題,2011年出現了這類算法的改進形式:一種基于通用模式的無波前自適應光學系統算法(參見Huang.Linhai and C.Rao,Wavefront sensorless adaptive optics:a general model-based approach,Optics Express,19,371-379,2011),該算法首次將相機像素灰度與坐標距離構成的二階矩MDS與入射波前斜率的平方均值SM建立了線性近似關系,對于由N階像差模構成的入射波前像差的一次校正僅需N+1次遠場測量;且對于大小不同像差采用同一校正算法流程。由于此類算法兩次像差校正延時(Δt=NT)隨像差模式階數N的增加而增大;因此這類算法的時間相關性差,在動態波前像差校正應用中,像差校正性能退化,系統收斂速度變慢。
基于通用模式的無波前傳感自適應光學系統,對動態波前校正能力退化的根本原因:波前像差模式基函數的斜率函數不正交存在耦合,使得波前任一像差模式的系數不能在相應模式對應的擾動電壓施加于變形鏡后得到其近似解析值,必須在所有像差模式對應的電壓擾動逐一施加于變形鏡后,根據權利要求1步驟4中的關系通過矩陣與向量的運算才能復原出相應的像差模式系數,完成像差的一次有效校正;即N次擾動一次校正的異步迭代校正機制。因此要解決上述系統方法的延時不確定性問題,核心在于正交化像差模式的斜率相關矩陣,可尋找像差模式基函數及其斜率函數正交的基函數,通常像差模式的基函數正交,但其斜率函數不一定正交,因此這種方法增加了像差模式基函數的約束條件,增大了系統實現的數學求解難度。而將現有通用的像差模式基函數斜率相關矩陣CN進行SVD分解,逆向正交并重構基函數是一種可行且簡單實用的途徑。
技術實現要素:
本發明要解決的技術問題是:克服現有技術的不足,突破基于通用模式基函數的無波前自適應光學系統相鄰像差校正延時(Δt=NT)隨波前像差模式數增加,相機采樣的遠場光強的二階矩與校正模式擾動相關性變差,系統收斂變慢,校正效果變差等問題。在像差斜率平方均值SM與遠場二階矩MDS近似線性的基礎上,正交化像差模式基函數間的斜率相關矩陣,將相鄰兩次像差校正的延時固定為Δt=T,從而改善系統時間相關性,使系統適用于動態像差的校正應用。
本發明解決上述技術問題采用的技術方案是:一種基于模式的同步無波前自適應光學系統,該系統主要由波前校正單元變形鏡、聚焦透鏡、遮攔小孔、遠場探測相機、控制器和高壓放大器構成,相機探測遠場光強分布形成反饋控制信號,控制器完成遠場反饋信號的數據處理與控制算法,獲取當前時刻的遠場二階中心矩及其增量,根據線性近似關系復原出波前畸變中含有的與擾動電壓所對應的像差模式的系數,利用變形鏡影響函數與模式基函數的關系矩陣,將復原出的模式系數轉換成電壓信號,經高壓放大器放大并施加于變形鏡形成像差閉環校正,工作步驟如下:
步驟1:離線計算校正的像差模式基函數Fi(x,y)的斜率相關矩陣CN,對CN奇異值SVD分解并構造新的模式基函數將原模式基函數斜率相關矩陣K對角化為L,像差Φ(x,y)表示為:
其中vi為像差模式基函數的系數,VM是在模式基數集FM下各模式對應的系數矢量。
模式基函數斜率相關矩陣K為:
其元素定義為:
其中S為光瞳面積;
模式基函數斜率相關矩陣K的SVD分解為:
L=C-1K(C-1)T (4)
新的像差模式函數為:
其中FN為N階像差模式基函數;
新的模式基函數的斜率相關矩陣為:
其元素的定義為:
步驟2:控制器在線隨機產生多組不同干擾強度的像差,計算并記錄每組像差的斜率的平方均值SM,
其中S為光瞳面積;
通過像差與變形鏡影響函數矩陣,將隨機產生的波前像差轉換為電壓信號,經高壓放大器放大后逐一施加于變形鏡。
步驟3:遠場探測相機采樣每組隨機像差施加于變形鏡后的光強分布,計算并記錄光強分布的二階中心矩MDS,
其中P,Q分為遠場光強分布相機采樣的行數與列數,I(i,j)為靶面像素的灰度值,R為遠場提取半徑。
步驟4:對步驟2記錄的多組SM和步驟3記錄的多組MDS進行線性擬合,獲取系統的SM與MDS的近似線性常量C0,
SM≈C0(1-MDS) (10)
步驟5:對變形鏡施加αGi(x,y)對應的擾動電壓,相機采樣遠場光強,控制器計算MDS的增量M,利用步驟4的線性關系和步驟2中式(8)表示的關系獲取入射波前像差中含有Gi(x,y)的像差模式系數vi,
并將其轉換為電壓信號經高壓放大器后作用于變形鏡,完成對變形鏡施加一次αGi(x,y)模式像差擾動后,一次Gi(x,y)像差的有效校正的同步迭代機制。
步驟6:重復步驟5的同步校正機制,對變形鏡施加所有像差模式Gi(x,y)(i=1,2…N)對應的電壓擾動并校正相應模式像差,完成一個像差校正周期的迭代,視遠場分布情況決定是否重復步驟5與步驟6的同步校正流程。
進一步的,所述的控制器只需完成相機采樣的遠場光強信號的二階矩MDS的計算,系統涉及的模式重構,波前像差斜率相關矩陣獲取及電壓與變形鏡影響函數矩陣計算等高維度矩陣運算可事先離線完成,極大減小了控制器的運算復雜度和內存要求,為控制器的小型化、輕量化及低功耗的嵌入式系統實現創造了條件。
進一步的,所述的算法對波前斜率相關矩陣實現了解耦合和對角化,對變形鏡施加一次像差模式的擾動后,完成一次相應像差模式的同步校正,因此相鄰兩次像差校正的延時取決于一次電壓擾動時間和相機采樣周期,而與像差模式的階數N無關;極大地改善了系統時域相關性,提高了系統對動態像差的校正能力,擴展了其應用領域。
進一步的,所述的校正單元變形反射鏡可以根據應用場合替換成其他的像差校正元件,可以選擇液晶校正器、分離式校正元件,系統采用的像差校正元件無具體限制;所述的相機也可以是其他面陣光電探測器,系統構成元件可靈活替換,因而擴展了其應用范圍。
進一步的,通過正交化波前模式基函數斜率相關矩陣,重構新的像差模式基函數,將相鄰兩次波前像差校正延時縮短為Δt=T,實現一次模式擾動一次相應像差模式校正的同步校正迭代機制,解決了已有系統校正延時隨像差模式數N增加的問題,適用于動態像差校正的應用。
本發明與現有技術相比的優點是:
(1)減少了相鄰兩次波前像差校正的延時,改善了系統的時間相關性;
(2)由于正交化波前模式基函數斜率相關矩陣,將波前模式復原中的矩陣運算轉換為標量運算,降低了系統對控制器數據處理能力和系統存儲器的要求;
(3)一次擾動一次校正的同步校正迭代機制,適用于動態像差的校正;
(4)系統的校正單元和光電探測器可靈活替換,改善了系統應用適應性,擴展其應用領域。
綜上所述,本發明在對對整體系統改變不大的情況下,能夠充分地利用正交化帶來的小延時,低運算復雜度,離線處理等優點,使同步迭代校正機制更適用于動態像差校正;而且系統結構簡單緊湊,實現容易,使本發明具有廣闊的應用前景。
附圖說明
圖1為本發明裝置的組成及原理示意圖;
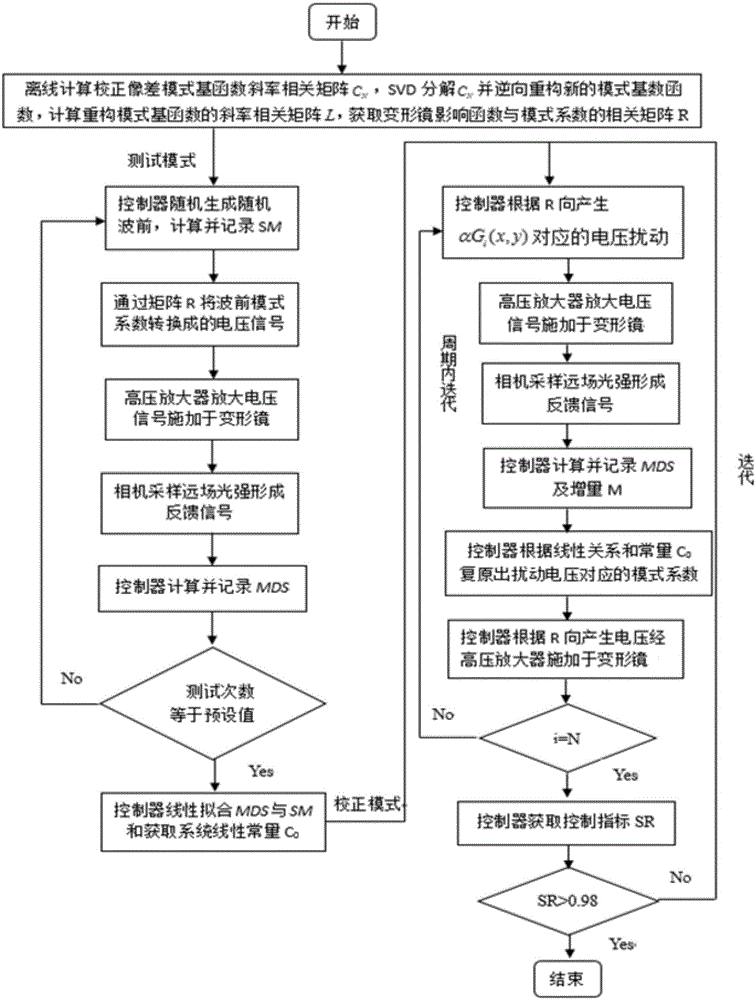
圖2系統像差校正流程;
圖3像差模式基函數的斜率相關矩陣正交化實例,其中,圖3(a)為原算法各像差模式的斜率相關矩陣,圖3(b)為重構像差模式的斜率相關矩陣;
圖4系統靜態像差校正實施實例結果;
圖5系統動態像差校正實施實例時域結果;
圖6系統動態像差校正實施實例帶寬特點。
具體實施方式
下面結合附圖和實施實例對本發明進行進一步說明。實施實例的主要條件,入射波前像差由18階澤尼克多項式組成的除平移和傾斜的像差,即像差模式基函數Fi(x,y)為Zi(x,y)(i=3~20),其系數遵從kolmogrov功率譜且隨機生成。動態像差校正應用時,風速為3m/s,干擾強度D/r=5。
圖1為本發明的系統組成,主要由波前校正單元變形反射鏡1、聚焦透鏡2、遮攔小孔3、遠場探測相機4、控制器5和高壓放大器6構成。圖2為系統像差校正算法的流程圖,主要分為離線數據處理與實時處理。圖3是實施實例中通過離線計算獲取的入射波前模式基函數斜率相關矩陣K和重構模式基函數斜率相關矩陣L。圖4為實施實例中系統采用傳統算法和本發明方法對靜態像差校正效果的對比。圖5和圖6分別為實施實例中傳統方法和本發明方法在動態像差校正迭代中的斯特列爾比SR和像差功率譜分析。具體實施步驟如下:
步驟1:離線計算校正的像差模式基函數Zi(x,y)的斜率相關矩陣CN,對CN奇異值SVD分解并構造新的模式基函數數將原模式基函數斜率相關矩陣K對角化為L,相應的K、L陣的如圖3所示。具體的,像差Φ(x,y)表示為:
其中vi為澤尼克像差模式基函數的系數,VM是在模式基數集ZM下各模式對應的系數矢量。模式基函數斜率相關矩陣K為:
其元素定義為:
其中S為光瞳面積;
模式基函數斜率相關矩陣K的SVD分解為:
L=C-1K(C-1)T (4)
新的像差模式基函數為:
其中ZN為N階澤尼克像差模式基函數;
新的模式基函數的斜率相關矩陣為:
其元素的定義為:
其中S為光瞳面積;
步驟2:控制器在線隨機產生500組不同干擾強度的像差,計算并記錄每組像差的斜率的平方均值SM,
通過像差與變形鏡影響函數矩陣,將隨機產生的波前像差轉換為電壓信號,經高壓放大器放大后施加于變形鏡。
步驟3:遠場探測相機采樣每組隨機像差施加于變形鏡后的光強分布,計算并記錄光強分布的二階中心矩MDS,
其中P,Q分為遠場光強分布相機采樣的行數與列數,I(i,j)為靶面像素的灰度值,R為遠場提取半徑。
步驟4:對步驟2記錄的多組SM和步驟3記錄的多組MDS進行線性擬合,獲取系統的SM與MDS的近似線性常量C0=1.2e4
SM≈C0(1-MDS), (10)
步驟5:對變形鏡施加αGi(x,y)對應的電壓(α=0.02),相機采樣遠場光強,控制器計算MDS的增量M,利用步驟4的線性關系和步驟2中式(8)表示的關系獲取入射波前像差中含有Gi(x,y)的像差模式系數vi,
并將其轉換為電壓信號經高壓放大器后作用于變形鏡,完成對變形鏡施加一次αGi(x,y)模式像差擾動后,一次Gi(x,y)像差的有效校正的同步迭代機制。
步驟6:重復步驟5的同步校正機制,對變形鏡施加所有像差模式Gi(x,y)(i=3~20)對應的電壓擾動并校正相應模式像差,完成一個像差校正周期的迭代,若系統的斯特列爾比SR小于0.98時,重復步驟5與步驟6的同步校正流程。
在圖4所示的靜態像差實施實例的結果可知,本發明的方法結果(method1所示圖例)除在第一個校正迭代周期中略弱于傳統方法外,后續校正迭代周期都優于傳統方法(method2所示圖例),隨著像差的增大,其優勢更為明顯。圖5和圖6所示的動態像差校正實施實例時域SR和頻域功率譜結果可知,本發明實施方法的SR隨時間的波動幅值小于傳統方法,系統校正殘差功率譜明顯優于傳統的方法的結果,其等效控制帶寬提高了2~3倍,根據相關理論可知,本發明的方法具有更好的校正性能,并適用于動態像差的校正。
以上所述,僅為本發明中的具體實施方式,但本發明的保護范圍并不局限于此,任何熟悉該技術的人在本發明所揭露的技術范圍內,可理解想到的變換或替換,都應涵蓋在本發明的包含范圍之內。
- 還沒有人留言評論。精彩留言會獲得點贊!