一種露天礦邊坡形狀優化設計方法與流程
本發明屬于露天礦山邊坡工程技術領域,具體涉及一種露天礦邊坡形狀優化設計方法。
背景技術:
我國的大中型露天礦多建于20世紀50~60年代,多數已進入深凹開采,過大的剝采比已使許多礦山陷入困境,尋求減少廢石剝離量的工作日益受到人們的重視。
一方面,隨著開采深度的增加和邊坡的加高加陡,邊坡的破壞概率和開采難度增大,另一方面,在開采中提高邊坡角,將大大減少剝離量,經濟效益十分可觀。因此,如何協調這二者的關系,設計出最優的邊坡角,是每個露天礦山面臨的難題,這將對礦山的生產安全和經濟效益產生重大影響。
目前采用的方法主要是極限平衡法(如各種類型的條分法)和數值計算分析(如元強度折減法)。采用極限平衡法分析時,坡面開挖形狀一般為直線型,在計算安全系數時,還要假設和搜索臨界滑裂面,安全系數可以寫成關于臨界滑裂面的函數,求最小安全系數即為求該函數的最小值,該函數具有非凸性和多極值性,前者阻礙了常規數學方法的使用,后者使搜索方法容易陷入局部最小值,因此很難確定極限狀態,而數值分析最大的困難是如何確定邊坡處于極限狀態,即失穩判據的確定目前尚無更好的方法,目前只能通過人為判斷和試算的辦法進行分析評價。
技術實現要素:
針對現有技術的不足,本發明的目的在于提供一種科學合理,效果佳的露天礦邊坡形狀優化設計方法,該方法由滑移線場理論計算的極限坡面曲線與邊坡坡面線相交于坡腳作為邊坡極限狀態的判斷依據來確定極限坡角αcr,通過擬合坡高H和極限坡角αcr來確定露天礦邊坡形狀。
為實現上述目的,本發明采用的技術方案是:一種露天礦邊坡形狀優化設計方法,其特征是,它包括以下內容:
1)計算極限坡角αcr:
(1)對特定坡高H和坡角α,由滑移線場理論計算極限狀態下的邊坡坡面曲線,簡稱為極限坡面曲線,設坡頂為坐標原點,坡體一側為x軸正半軸,向下為y軸正半軸;
(2)Mα(xα,yα,θα,σα)為第α族滑移線上的點,Mβ(xβ,yβ,θβ,σβ)為第β族滑移線上的點,由公式(1-1)~(1-4)解得滑移線場上的點M(x,y,θ,σ),其中,x為橫坐標值,y為縱坐標值,θ為最大主應力σ1與x軸交角,σ為特征應力,為兩族滑裂面交角平均值:
(3)計算極限坡面曲線:Mb(xb,yb,θb,σb)為極限坡面曲線已知點,M′β(x′β,y′β,θ′β,σ′β)為第β族滑移線上的已知點,由公式(2-1)~(2-4)解得極限坡面曲線上點Mij(xij,yij,θij,σij):
(4)邊界條件為:主動區OAB邊界條件:主動區第α、β族已知計算點Mα和Mβ的橫坐標x=Δx·i,Δx為計算步長,i為自然數,i=0~N1,N1為步長數,取N1=999,y=0,主動區邊界最大主應力與x軸交角主動區邊界特征應力P為坡頂荷載,滑移線交點計算公式為(1-1)~(1-4);被動區OCD邊界條件:被動區滑移線交點計算公式依然為(1-1)~(1-4),而極限坡面曲線,即OD線公式采用(2-1)~(2-4),Mb第一個已知點就是坡頂原點數值,坐標值(xb,yb)=(0,0),過渡區OBC邊界條件:過渡區滑移線交點計算公式依然為(1-1)~(1-4),而過渡區邊界點的特征應力為其中k為自然數,k=0~N2,Δθ=θΙΙΙ-θΙ,N2為過渡區點剖分數,為滿足Δθ≥0,則必須因此坡頂荷載最小值,當邊坡算例無外荷載時,對邊坡坡頂施加Pmin,此時即Δθ=0,取N2=0;
(5)計算極限坡面曲線與坡底地基線交點橫坐標x1,此時變換坐標系,設坡腳為坐標原點,向上為y軸正半軸,向邊坡體一側坡底地基線為x軸正半軸,當x1>0時,判斷邊坡處于穩定狀態,此時增大坡角α,并重復上述步驟(1)~(4);當x1=0時,即極限坡面曲線與邊坡坡面線相交于坡腳時,此時判斷邊坡處于極限狀態,坡角α為極限坡角αcr;當x1<0時,此時判斷邊坡處于破壞狀態;
2)將一系列的坡高H和極限坡角αcr擬合便得到露天礦邊坡最優化形狀,由敏感性分析可知,坡高H和坡角α變大時,邊坡穩定性降低,因此邊坡保持極限狀態時,坡高H變大,極限坡角αcr變小,由此可知,露天礦邊坡形狀優化設計結果為凸曲線;
3)礦山在進行坡面形狀優化設計時,要設定安全儲備系數,安全儲備系數的計算步驟為:
①首先由公式(3)對強度參數進行折減,
式中c為粘聚力,為摩擦角,Fi為折減系數,i為自然數;
②采用折減后的強度參數c1和由滑移線場理論計算極限坡面曲線;當x1>0時,判斷邊坡處于穩定狀態,此時增大Fi,當x1=0時,即極限坡面曲線與邊坡坡面線相交于坡腳時,判斷邊坡處于極限狀態,此時Fi為露天礦山邊坡安全儲備系數。
本發明的一種露天礦邊坡形狀優化設計方法與現有技術相比,本發明具有如下的有益效果:
(1)本發明采用極限坡面曲線與邊坡坡面線是否相交作為失穩判據,實現了失穩判據客觀標準定量化,避免了人為因素影響,保證了礦山生產的安全性;
(2)本發明的露天礦邊坡形狀優化設計以及安全儲備系數的計算相對于已有方法最大優勢是不必假設和搜索臨界滑裂面;
(3)由本發明設計的露天礦邊坡最優化形狀為凸曲線,相對于已有方法可以減少廢石剝離量,提高經濟效益,延長礦山壽命;
(4)其方法科學合理,效果佳。
附圖說明
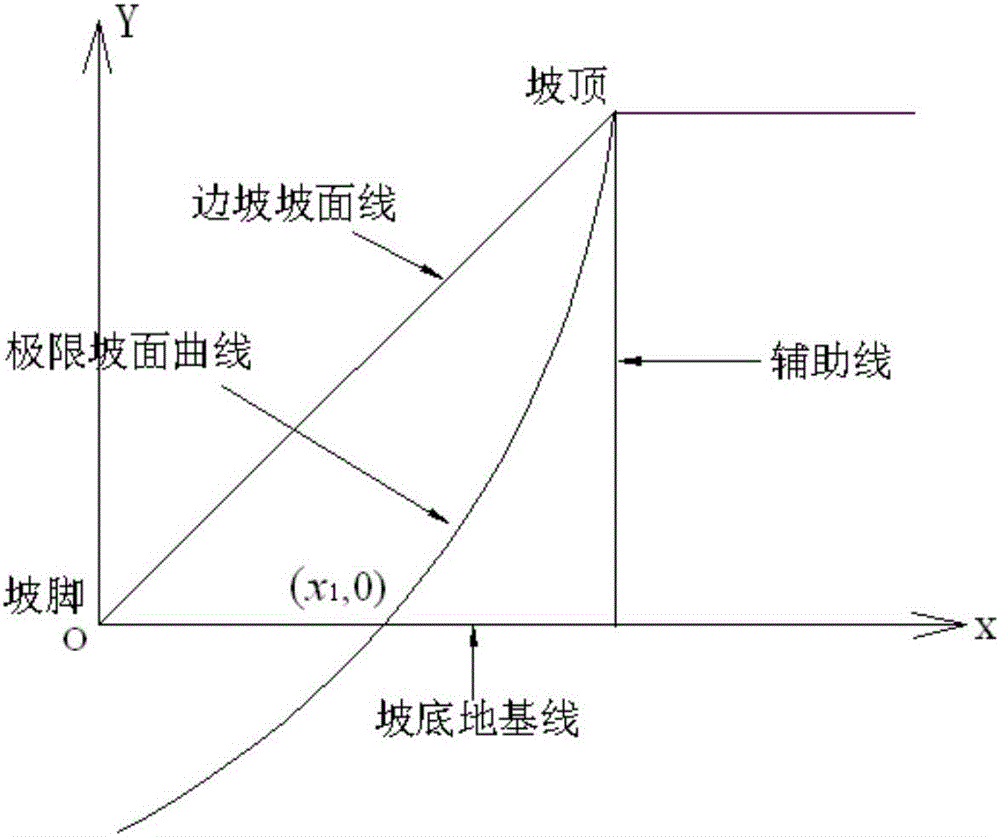
圖1是:滑移線場理論計算極限坡面曲線示意圖;
圖2是:x1>0時,邊坡處于穩定狀態示意圖;
圖3是:x1=0時,坡角α為極限坡角αcr示意圖;
圖4是:x1<0時,邊坡處于破壞狀態示意圖;
圖5是:本發明的露天礦邊坡形狀優化設計方法流程圖;
圖6是:本發明的露天礦邊坡形狀優化設計安全儲備系數計算流程圖;
圖7是:本發明的露天礦邊坡形狀優化設計方法設計的邊坡面形狀與現有Bishop法設計邊坡面形狀對比示意圖;
圖8是:本發明的露天礦邊坡形狀優化設計方法設計的邊坡面形狀與空間力學原理設計邊坡面形狀對比示意圖。
具體實施方式
下面結合附圖對本發明的具體實施方案做進一步的詳細說明。
本發明的一種露天礦邊坡形狀優化設計方法,包括以下內容:
1)計算極限坡角αcr:
(1)對特定坡高H和坡角α,由滑移線場理論計算極限狀態下的邊坡坡面曲線,簡稱為極限坡面曲線,設坡頂為坐標原點,坡體一側為x軸正半軸,向下為y軸正半軸,見圖1所示;
(2)Mα(xα,yα,θα,σα)為第α族滑移線上的點,Mβ(xβ,yβ,θβ,σβ)為第β族滑移線上的點,由公式(1-1)~(1-4)解得滑移線場上的點M(x,y,θ,σ),其中,x為橫坐標值,y)為縱坐標值,θ為最大主應力σ1與x軸交角,σ為特征應力,為兩族滑裂面交角平均值:
(3)計算極限坡面曲線:Mb(xb,yb,θb,σb)為極限坡面曲線已知點,M′β(x′β,y′β,θ′β,σ′β)為第β族滑移線上的已知點,由公式(2-1)~(2-4)解得極限坡面曲線上點Mij(xij,yij,θij,σij):
(4)邊界條件為:主動區OAB邊界條件:主動區第α、β族已知計算點Mα和Mβ的橫坐標x=Δx·i,Δx為計算步長,i為自然數,i=0~N1,N1為步長數,取N1=999,y=0,主動區邊界最大主應力與x軸交角主動區邊界特征應力P為坡頂荷載,滑移線交點計算公式為(1-1)~(1-4);被動區OCD邊界條件:被動區滑移線交點計算公式依然為(1-1)~(1-4),而極限坡面曲線,即OD線公式采用(2-1)~(2-4),Mb第一個已知點就是坡頂原點數值,坐標值(xb,yb)=(0,0),過渡區OBC邊界條件:過渡區滑移線交點計算公式依然為(1-1)~(1-4),而過渡區邊界點的特征應力為其中k為自然數,k=0~N2,Δθ=θΙΙΙ-θΙ,N2為過渡區點剖分數,為滿足Δθ≥0,則必須因此坡頂荷載最小值,當邊坡算例無外荷載時,對邊坡坡頂施加Pmin,此時即Δθ=0,取N2=0;
(5)計算極限坡面曲線與坡底地基線交點橫坐標x1,此時變換坐標系,設坡腳為坐標原點,向上為y軸正半軸,向邊坡體一側坡底地基線為x軸正半軸,當x1>0時,判斷邊坡處于穩定狀態,見圖2所示,此時增大坡角α,并重復上述步驟(1)~(4);當x1=0時,即極限坡面曲線與邊坡坡面線相交于坡腳時,此時判斷坡角α為極限坡角αcr,見圖3所示;當x1<0時,此時判斷邊坡處于破壞狀態,見圖4所示;
2)將一系列的坡高H和極限坡角αcr擬合便得到露天礦邊坡最優化形狀,由敏感性分析可知,坡高H和坡角α變大時,邊坡穩定性降低,因此邊坡保持極限狀態時,坡高H變大,極限坡角αcr變小,由此可知,露天礦邊坡形狀優化設計結果為凸曲線;
3)礦山在進行坡面形狀優化設計時,要設定安全儲備系數,安全儲備系數的計算步驟為:
①首先由公式(3)對強度參數進行折減,
式中c為粘聚力,為摩擦角,Fi為折減系數,i為自然數;
②采用折減后的強度參數c1和由滑移線場理論計算極限坡面曲線;當x1>0時,判斷邊坡處于穩定狀態,此時增大Fi,當x1=0時,即極限坡面曲線與邊坡坡面線相交于坡腳時,判斷邊坡處于極限狀態,此時Fi為露天礦山邊坡安全儲備系數。
第一道露天礦邊坡優化設計算例(方宏偉,李長洪,李波.均質邊坡穩定性極限曲線法[J].巖土力學,2014,35(Supp.1):156-164.)計算參數見表1,原設計基于Bishop法采用α=55°的直線邊坡形狀進行開挖,對應安全系數FOS=1.499。當取最大坡高H=128 m和α=55°及表1中的巖體參數,采用圖6計算安全儲備系數得F1=1.182,這是由于本方法計算安全系數時要在坡頂施加外荷載Pmin=990.5789kPa。因此,安全系數要比已有方法偏小。
表1.露天礦邊坡工程參數與安全系數計算結果
為便于與原設計方法作比較,這里采用坡頂處αcr=55°及F1=1.182折減后的強度參數根據圖5計算極限坡角αcr以及設計坡面形狀,計算參數與結果見表2,其中r為水平距離,見公式(4),
表2.與極限平衡法對比的本發明的露天礦邊坡優化設計結果
本發明的方法邊坡形狀優化設計結果與現有Bishop法設計邊坡面形狀對比見7圖,圖中第一點坐標為(r=0,H=0),
該實例的邊坡坡面優化形狀設計結果為上緩下陡凸曲線,相對于現有Bishop法設計邊坡面形狀,本發明優化設計結果避免了單一直線開挖,使廢石剝離量顯著減少。
第二道露天礦邊坡算例為本發明設計方法與空間力學原理相對比。
空間力學原理是根據極限平衡原理確定邊坡形狀的計算方法(朱乃龍,張世雄.巖石深凹邊坡穩定性坡角的初步確定方法[J].工程力學,20(5):130-133.),H與r關系式見公式(5),該理論由r設定值計算H,再由公式(6)計算αcr,其中r0=100m,為常數,
空間力學原理計算參數與結果見表3。
表3空間力學原理的露天礦邊坡優化設計結果
采用圖5的本發明優化設計方法對不同H對應的αcr計算結果見表4,r的計算見公式(7),
表4與空間力學原理對比的本發明的露天礦邊坡優化設計結果
邊坡形狀優化設計結果對比見下圖8,圖中第一點為坡腳,坐標為(r0=100,H=0),分析可知,本發明的方法與空間力學原理的邊坡形狀優化設計結果都是上緩下陡凸曲線,即隨著H的變大αcr變小,但由表3和表4對比可知,本發明的方法將αcr提高了3°~10°,因此按本發明的方法設計邊坡坡面形狀,可以明顯減少廢石剝離量。
通過兩個露天礦邊坡算例可知,本發明的露天礦邊坡優化設計方法給出的邊坡坡面形狀為凸曲線,相對于已有方法能夠減少剝離廢礦石,達到提高經濟效益,延長礦山壽命的目的。
最后應當說明的是,以上實施例僅用以說明本發明的技術方案而非對其限制,盡管參照上述實施例對本發明進行了詳細的說明,所屬領域的普通技術人員應當理解,依然可以對本發明的具體實施方式進行修改或者等同替換,而未脫離本發明精神和范圍的任何修改或者等同替換,其均應涵蓋在本發明的權利要求范圍當中。
- 還沒有人留言評論。精彩留言會獲得點贊!