一種地基承載力安全性的判別方法與流程
本發明屬于工程地基穩定性技術領域,具體涉及一種地基承載力安全性的判別方法。
背景技術:
地基承載力是地基土單位面積上隨荷載增加所發揮的承載潛力,常用單位Kpa,是評價地基穩定性的綜合性用詞。在目前實際工程中,地基承載力安全性分析對整個工程安全性來說都至關重要。大部分工程實踐中地基承載力安全性穩定分析多采用承載力安全系數法,即通過地基的極限承載力qf除以地基實際承載力q得到安全系數F,再進行安全性判別,具體如下式表示:
但該方法過于依賴工程經驗,沒有考慮到結構抗力和荷載效應的隨機性質,無法反映結構的實際失效狀態,更不能準確的反映土體破壞時的實質,在一定程度上存在理論缺陷,用來評價地基承載力安全性也是片面的,不合理的,在應用過程中存在一定的限制。
技術實現要素:
本發明的目的是提供一種地基承載力安全性的判別方法,解決了現有地基承載力安全性判斷過程中,參數過分依靠工程經驗,安全性判斷片面不準確的問題。
本發明一種地基承載力安全性的判別方法所采用的技術方案是,包括以下步驟:
步驟1,使用邊坡穩定分析中的強度安全系數法,將其應用到地基穩定分析中,定義新的安全系數F,具體如公式(1)-(3)所示,
ce=c/F (1)
fe=f/F (2)
其中,c為土的粘聚力,f為內摩擦系數,q為地基實際承載力,qf,e為折減后的地基極限承載力,ce為折減后的土的粘聚力,fe為折減后的內摩擦系數;
步驟2,以可靠度理論為基礎,建立可靠度指標β和步驟1中安全系數F的關系,如公式(4),
其中,μF為安全系數F的均值,σF為安全系數F的標準差;
當目標可靠度指標βa=3.7時,計算出可靠度指標β與安全系數允許值Fa;
步驟3,通過分別引入步驟1中安全系數F的相對安全率ηF、步驟2中可靠度指標β的相對安全率ηR,具體如公式(5)和(6)表示,
ηR=(β-βa)σF+1 (6)
進行步驟2中的安全系數允許值Fa的普適性驗證;當ηR≈ηF時,安全系數允許值Fa滿足普適性。
本發明的特征還在于,
步驟2具體為:
步驟2.1,通過在步驟1安全系數F基礎上建立極限平衡方法,得到的極限狀態方程式,如式(7),
G=F(x1,x2…xi)-1(i=1,2…n) (7)
其中,Xi為一組相互獨立的隨機變量,具體為步驟1中的粘聚力c和內摩擦系數f,
步驟2.2,通過采用一階二次距法計算步驟2中公式(4)的可靠度指標β,引入標準無量綱變量zi,如式(8),
其中,μx,i和σx,i分別為獨立變量粘聚力c、內摩擦系數f的均值和標準差;
步驟2.3,使用Taylor級數將步驟2.2中公式(8)在極限失效狀態點處展開,只保留常數項和一次項使功能函數線性化,然后計算出公式(8)在極限失效狀態點處的均值和標準差,按照公式(9)進而求解結構可靠度指標β,
步驟2.4,設定當目標可靠度指標βa=3.7時,根據地基參數,通過公式(7)-(9)計算出可靠度指標β與安全系數允許值Fa。
本發明的有益效果是:本發明一種地基承載力安全性的判別方法利用邊坡穩定分析中的強度折減安全系數法,通過不斷折減土體強度參數,直到地基在極限狀態下發生破壞從而得到地基穩定的安全系數;然后通過目標可靠度指標得到對應的安全系數允許值;最后進行安全系數允許值的普適性驗證,本發明解決了現有地基承載力安全性判斷過程中,參數過分依靠工程經驗,安全性判斷片面不準確的問題,步驟簡單,在工程地基安全穩定性方面有很好的實用價值。
附圖說明
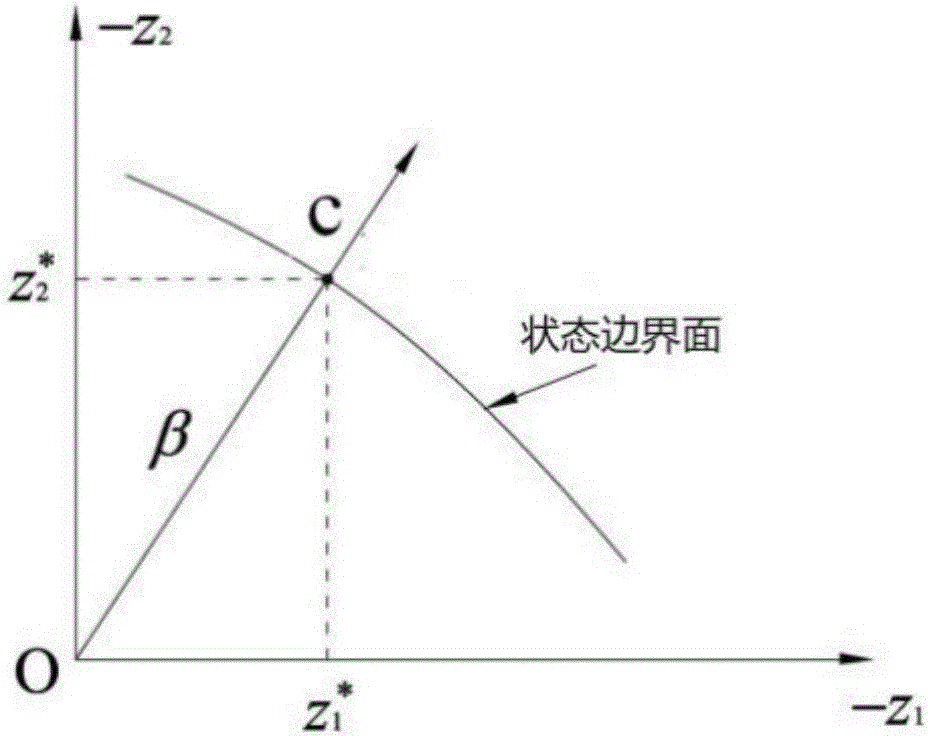
圖1是本發明實施例中可靠度指標β的幾何意義示意圖;
圖2是本發明實施例中地基承載力分析結構示意圖;
圖3是本發明實施例中表2的線性擬合回歸曲線示意圖;
圖4是本發明實施例中表2的線性擬合回歸曲線示意圖;
圖5是本發明實施例中不同土體容重γ2對應的ηF~ηR線性回歸示意圖;
圖6是本發明實施例中不同內摩擦系數f對應的ηF~ηR線性回歸示意圖;
圖7是本發明實施例中不同土體粘聚力c對應的ηF~ηR線性回歸示意圖。
具體實施方式
下面結合附圖和具體實施方式對本發明進行詳細說明。
本發明一種地基承載力安全性的判別方法,具體包括以下步驟:
步驟1,使用邊坡穩定分析中的強度安全系數法,將其應用到地基穩定分析中,定義新的安全系數F,具體如公式(1)-(3)所示,
ce=c/F (1)
fe=f/F (2)
其中,c為土的粘聚力,f為內摩擦系數,q為地基實際承載力,qf,e為折減后的地基極限承載力,ce為折減后的土的粘聚力,fe為折減后的內摩擦系數;
步驟2,以可靠度理論為基礎,建立可靠度指標β和步驟1中安全系數F的關系,如公式(4),
其中,μF為安全系數F的均值,σF為安全系數F的標準差;
當目標可靠度指標βa=3.7時,計算出可靠度指標β與安全系數允許值Fa;
步驟3,通過分別引入步驟1中安全系數F的相對安全率ηF、步驟2中可靠度指標β的相對安全率ηR,具體如公式(5)和(6)表示,
ηR=(β-βa)σF+1 (6)
進行步驟2中的安全系數允許值Fa的普適性驗證;當ηR≈ηF時,安全系數允許值Fa滿足普適性。
步驟2具體為:
步驟2.1,通過在步驟1安全系數F基礎上建立極限平衡方法,得到的極限狀態方程式,如式(7),
G=F(x1,x2…xi)-1(i=1,2…n) (7)
其中,Xi為一組相互獨立的隨機變量,具體為步驟1中的粘聚力c和內摩擦系數f,
步驟2.2,通常采用一階二次距法計算步驟2中公式(4)的可靠度指標β,引入標準無量綱變量zi,如式(8),
其中,μx,i和σx,i分別為獨立變量粘聚力c、內摩擦系數f的均值和標準差;
步驟2.3,使用Taylor級數將步驟2.2中公式(8)在極限失效狀態點處展開,只保留常數項和一次項使功能函數線性化,然后計算出公式(8)在極限失效狀態點處的均值和標準差,按照公式(9)進而求解結構可靠度指標β,
步驟2.4,設定當目標可靠度指標βa=3.7時,根據地基參數,通過公式(7)-(9)計算出可靠度指標β與安全系數允許值Fa。
實施例
目前建筑地基基礎設計規范(GB50007-2011)規定承載力安全系數允許值Fa為2-3,而水利水電工程邊坡設計規范(SL386-2007)規定不同等級邊坡穩定安全系數Fa在1.1-1.3內,顯然邊坡穩定安全系數要比承載力安全系數更為安全,因此我們將邊坡穩定分析方法應用到地基承載力安全穩定分析中來。
(1)定義新的安全系數F
使用邊坡穩定分析中的強度安全系數法,將其應用到地基承載力安全性穩定分析中,定義新的安全系數F,具體如公式(1)-(3)所示,
ce=c/F (1)
fe=f/F (2)
其中,c為土的粘聚力,f為內摩擦系數,q為地基實際承載力,qf,e為折減后的地基極限承載力強度,ce為折減后的土的粘聚力,fe為折減后的內摩擦系數。
(2)建立可靠度指標β和安全系數F的關系,當目標可靠度指標βa=3.7時,計算出可靠度指標β與安全系數允許值Fa。
為了克服結構抗力和荷載效應的隨機性質帶來的影響,引入可靠度理論,以可靠度理論為基礎,建立可靠度指標β和安全系數F的關系,如公式(4),
其中,μF為安全系數F的均值,σF為安全系數F的標準差;
通過在安全系數F基礎上建立極限平衡方法,得到的極限狀態方程式,如式(7),
G=F(x1,x2…xi)-1(i=1,2…n) (7)
其中,Xi為一組相互獨立的隨機變量,具體為步驟1中的粘聚力c和內摩擦系數f;
通過采用一階二次距法計算所述的步驟2中公式(4)的可靠度指標β,引入標準無量綱變量zi,如式(8),
其中,μx,i和σx,i分別為獨立變量粘聚力c、內摩擦系數f的均值和標準差;
如圖1所示,原點O代表均值點,是隨機變量最有可能的數值;點C代表極限失效狀態點,即為標準化空間設計驗算點;線段OC的長度即為可靠度指標β,物理意義是隨機變量從最有可能的數值過渡到破壞面的最短距離。
使用Taylor級數將點C極限失效狀態點處展開,只保留常數項和一次項使功能函數線性化,然后計算出公式(8)在極限失效狀態點處的均值和標準差,按照公式(9)進而求解結構可靠度指標β。
如表1的所示,根據《水利水電工程結構可靠度設計統一標準》(簡稱水工統標)對水利工程中不同安全級別結構的允許可靠度指標的規定,表中第一類破壞指非突發性破壞;第二類破壞指突發性破壞,無明顯征兆,一旦發生事故難于補救或修復,將水利工程結構破壞歸于第二類,一般地基失事的后果較大壩等重要設施要小,因此,設定目標可靠度指標βa=3.7較為合適。
表1 水工統標規定的結構允許可靠度指標βa
設定當目標可靠度指標βa=3.7時,如圖2所示,參考具體地基參數,包括基礎寬度B=10m,埋深D=1.5m,γ1=9KN/m3,土體容重γ2=19KN/m3。土體的粘聚力均值μc=20KPa,μf=0.46,地基實際承載力q=600KN/m2,強度系數均取設計值,通常可取0.2分位設計值,強度參數按公式(10)取值:
xk=μk-0.842σk (10)
式中,xk代表強度指標土體粘聚力c和內摩擦系數f,下標k代表各強度指標的標準值,μk和σk分別為變量x的均值和標準差。
通過現有的地基承載力定義的承載力安全系數法所對應的功能函數,具體為公式(11)-(15),采用一次二階矩法進行可靠度分析計算及安全系數計算,可得F原始=2.3。
qf=cNC+γ1DNq+0.5Bγ2Nr (12)
其中,q為地基實際承載力,qf為地基極限承載力;c、γ1、γ2分別為土的粘聚力、重度及基礎土體容重;Nc、Nq、Nr均為地基承載力系數;B為基礎寬度,D為埋深,為內摩擦角。
通過本發明定義的安全系數對應的功能函數公式(7)、采用一次二階矩法進行可靠度分析計算及安全系數計算,可得安全系數允許值Fa=1.35,計算結果具體為表2所示:
表2 不同地基寬度B地基安全性計算成果
注:方案1-現有計算法,方案2-本發明計算法。
計算結果表明,在βa=3.7時,邊坡穩定分析所得到的安全系數允許值Fa=1.35與現有的地基承載力分析所得的安全系數F原始=2.3數值上存在明顯差異,但計算的可靠度指標β相同均為3.69,3.69與目標可靠度指標βa=3.7近似相同,這是因為兩種定義方式實際上對應著相同的極限狀態方程,因此得到了相同的可靠指標,反映了相同的可靠度,同時得出了在允許可靠度指標βa=3.7時相對應的安全系數允許值Fa=1.35。
(3)通過對比ηF和ηR的大小,當ηR≈ηF時,安全系數允許值Fa滿足普適性。
當地基寬度B發生改變時,計算所得的可靠度指標β≠3.7,采用方案1和方案2計算所得的安全系數也不為2.3和1.35,為了驗證不同的地基寬度B計算得出的安全系數與可靠度指標是否能反映了相同的風險控制水平,引入土石壩和重力壩抗滑穩定分析判據“相對安全率”的概念,建立了安全系數與可靠指標之間的關系,引入安全系數F的相對安全率ηF、可靠度指標β的相對安全率ηR,具體如公式(5)和(6)表示,
ηR=(β-βa)σF+1 (6)
對于不同的地基寬度B,分別如表2中列(4)和(6)所示,線性相關擬合情況如圖3和圖4所示,方案1和方案2所得到曲線的斜率均約為1,擬合系數均約為1,表明對于任何情況均滿足ηR≈ηF的成立,說明安全系數允許值Fa具有很好的適用性。
除改變地基寬度B驗證安全系數允許值Fa的普適性外,當其他變量變化時:(1)土體容重γ2以0.5(kN·m-3)的增量由17(kN·m-3)逐漸增加至21.5(kNm-3);(2)內摩擦系數f以0.025的增量從0.385逐漸增加至0.610;(3)土體粘聚力c以1kPa的增量由15kPa逐漸增至24kPa,將變量(1)-(3)計算出的安全系數F相對安全率ηF與可靠度指標β相對安全率ηR進行線性相關擬合,分別得到相應的相對安全率ηF和ηR的回歸曲線關系,如圖5-7所示,安全系數相對安全率ηF與可靠度指標相對安全率ηR依然具備較好的相關性。由此可證明,在任意強度參數的地基工況中,邊坡穩定分析下的安全系數允許值與相對應的可靠指標反映了相同的風險控制水平,并且驗證了在允許可靠度指標βa=3.7時相對應的安全系數允許值Fa=1.35滿足普適性。
本發明利用邊坡穩定分析中的強度折減安全系數法,通過不斷折減土體強度參數,直到地基在極限狀態下發生破壞從而得到地基穩定的安全系數;然后通過目標可靠度指標得到對應的安全系數允許值;最后進行安全系數允許值的普適性驗證,本發明解決了現有地基承載力安全性判斷過程中,參數過分依靠工程經驗,安全性判斷片面不準確的問題,步驟簡單,在工程地基安全穩定性方面有很好的實用價值。
- 還沒有人留言評論。精彩留言會獲得點贊!