一種基于邊光滑的矢量有限元電磁計算方法與流程

本發明屬于工程計算電磁學，具體涉及一種基于邊光滑的矢量有限元電磁計算方法。

背景技術：

1、矢量有限元方法被提出以來，已構建起堅實的理論與實踐基礎，尤其是在電磁學計算中占據核心地位，用于精確分析復雜環境中的電磁場，主要分為基于電場e求解的高頻電磁場問題和基于磁矢勢a求解的非線性渦流問題。

2、基于高頻電磁場問題，由于狀態變量為電場，而磁場需要對電場進行求導，磁場和電場求解精度的不同往往會引發系列數值問題。目前，采用結構化網絡或采用高階單元插值函數提高計算精度。前者是通過四邊形或六面體對求解域進行網格劃分，并基于四面體或六面體網格的高階連續來提高變量求導精度，但其在復雜幾何邊界處理上存在一定局限性；后者是通過高階三角形或高階四面體單元進行插值函數構造，利用提高差值函數階次以提高變量求解和求導計算精度，但其在計算過程中自由度數量倍增，增加了對計算資源的需求，進而導致矩陣求解速度近似指數下降。

技術實現思路

1、本發明在于提供一種基于邊光滑的矢量有限元電磁計算方法，通過構建電磁場的邊光滑的矢量有限元弱形式，能夠在不增加自由度數量的前提下，顯著提高了電磁場求解精度，節約了計算資源。同時，能夠適用于結構化和非結構化網絡，進而維持有限元在復雜幾何邊界上的解析精度，對于混合網格有較好的適配性；能夠大幅度改善矢量有限元在計算電磁學中的分析能力，具有較好的拓展性和適配性。

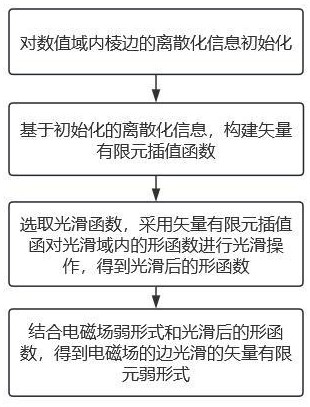
2、一種基于邊光滑的矢量有限元電磁計算方法，包括如下步驟：

3、對數值域內棱邊的離散化信息初始化；

4、基于初始化的離散化信息，構建矢量有限元插值函數；

5、選取光滑函數，采用矢量有限元插值函對光滑域內的形函數進行光滑操作，得到光滑后的形函數；

6、結合電磁場弱形式和光滑后的形函數，得到電磁場的邊光滑的矢量有限元弱形式。

7、通過構建電磁場的邊光滑的矢量有限元弱形式，能夠在不增加自由度數量的前提下，顯著提高了電磁場求解精度，節約了計算資源。同時，能夠適用于結構化和非結構化網絡，進而維持有限元在復雜幾何邊界上的解析精度，對于混合網格有較好的適配性；能夠大幅度改善矢量有限元在計算電磁學中的分析能力，具有較好的拓展性和適配性。

8、進一步的，離散化信息包括網格離散化信息和自由度離散化信息。

9、進一步的，對數值域內棱邊的離散化信息初始化的過程具體包括如下步驟：

10、基于預設的幾何模型和網格劃分參數，對求解域進行網格劃分；

11、基于劃分網格，對網格信息進行離散化；

12、基于劃分網格，對自由度信息進行離散化。

13、進一步的，基于劃分網格，對網格信息進行離散化的過程具體包括：

14、對每個節點分配唯一的編號，并記錄其全局坐標，表示為：編號-坐標；

15、對每個棱邊分配唯一的編號，并依照順序記錄其關聯的節點和單元，表示為：編號-節點-單元；

16、對每個單元分配唯一的編號，并依照順序記錄其包含的棱邊和節點，表示為：編號-棱邊-節點。

17、進一步的，基于劃分網格，對自由度信息進行離散化的過程具體包括：

18、將自由度分配給每個棱邊，并記錄其關聯的棱邊，表示為：編號-棱邊。

19、進一步的，矢量有限元插值函數是指離散化信息結合矢量有限元理論所得的單元內的插值函數，其表達式為：

20、；

21、式中，表示單元內某一點的電場強度；表示在單元、局部編號為的棱邊上的矢量插值函數或形函數，即，表示單元、局部編號為的棱邊上形函數的標量部分；表示單元、局部編號為的棱邊上形函數的單位矢量；表示在單元、局部編號為的棱邊上的自由度的值，即為待求解場變量。

22、進一步的，選取光滑函數，采用矢量有限元插值函對光滑域內的形函數進行光滑操作，得到光滑后的形函數的過程具體包括如下步驟：

23、將計算域劃分為多個以選定棱邊為重心的多面體不重疊的子光滑域，且各子光滑域之間互斥；

24、基于選定棱邊和其對應的光滑域，選取光滑函數；

25、基于插值函數和矢量插值函數，求解旋度和散度；

26、對形函數的標量部分的梯度算子進行光滑操作，得到光滑后的形函數。

27、進一步的，光滑后的形函數包括：

28、光滑后的旋度，其表達式為：

29、；

30、光滑后的散度，其表達式為：

31、；

32、式中，為哈密頓算符；表示單元的光滑域；表示單元的光滑函數，其表達式為： =1。

33、進一步的，結合電磁場弱形式和光滑后的形函數，構建電磁場的邊光滑的矢量有限元弱形式的過程具體包括如下步驟：

34、構造電磁場頻域方程；

35、選取形函數為權函數，在求解域內做加權積分，并采用矢量分析和高斯公式將二階旋度體積分轉變為一階旋度體積分和相應的面積分，得到電磁場頻域方程的弱形式；

36、采用插值函數對電磁場頻域方程的弱形式進行離散，得到選定棱邊的弱形式；

37、基于光滑后的形函數對選定棱邊的弱形式進行邊光滑，得到邊光滑的矢量有限元弱形式。

38、進一步的，邊光滑的矢量有限元弱形式的表達式為：

39、；

40、；

41、式中，表示單元的求解域；表示相對磁導率，其作為權函數；表示單元的光滑域；表示單元、局部編號為的棱邊上形函數的標量部分；表示單元的光滑函數；表示單元、局部編號為的棱邊上形函數的單位矢量；表示真空波數；表示相對介電常數；表示虛單位；表示電導率；表示角頻率；表示真空中的電容率；表示單元、局部編號為的棱邊上形函數的標量部分；表示單元、局部編號為的棱邊上的自由度的值；為第三類邊界條件相關函數，當未施加邊界條件時，；表示單元代表的求解域對應邊界；表示單元的邊界上的法向向量。

42、本發明的有益效果為：

43、本發明通過構建電磁場的邊光滑的矢量有限元弱形式，能夠在不增加自由度數量的前提下，利用梯度光滑理論顯著提高了電磁場求解精度，節約了計算資源。同時，能夠適用于結構化和非結構化網絡，進而維持有限元在復雜幾何邊界上的解析精度，對于混合網格有較好的適配性；能夠大幅度改善矢量有限元在計算電磁學中的分析能力，具有較好的拓展性和適配性。能夠在傳統矢量有限元求解框架中嵌入邊光滑理論，對于原有理論方法做到最小改動，便于對已有矢量有限元程序的合理利用和拓展。采用邊光滑理論，能夠降低矢量有限元對網格質量的要求，可以適配更復雜的模型幾何，使矢量有限元可以使用于更復雜的問題。

技術特征：

1.一種基于邊光滑的矢量有限元電磁計算方法，其特征在于，包括如下步驟：

2.根據權利要求1所述的一種基于邊光滑的矢量有限元電磁計算方法，其特征在于，離散化信息包括網格離散化信息和自由度離散化信息。

3.根據權利要求2所述的一種基于邊光滑的矢量有限元電磁計算方法，其特征在于，對數值域內棱邊的離散化信息初始化的過程具體包括如下步驟：

4.根據權利要求3所述的一種基于邊光滑的矢量有限元電磁計算方法，其特征在于，基于劃分網格，對網格信息進行離散化的過程具體包括：

5.根據權利要求3所述的一種基于邊光滑的矢量有限元電磁計算方法，其特征在于，基于劃分網格，對自由度信息進行離散化的過程具體包括：

6.根據權利要求3所述的一種基于邊光滑的矢量有限元電磁計算方法，其特征在于，矢量有限元插值函數是指離散化信息結合矢量有限元理論所得的單元內的插值函數，其表達式為：

7.根據權利要求6所述的一種基于邊光滑的矢量有限元電磁計算方法，其特征在于，選取光滑函數，采用矢量有限元插值函對光滑域內的形函數進行光滑操作，得到光滑后的形函數的過程具體包括如下步驟：

8.根據權利要求7所述的一種基于邊光滑的矢量有限元電磁計算方法，其特征在于，光滑后的形函數包括：

9.根據權利要求8所述的一種基于邊光滑的矢量有限元電磁計算方法，其特征在于，邊光滑的矢量有限元弱形式的表達式為：

技術總結
本發明屬于工程計算電磁學技術領域，具體涉及一種基于邊光滑的矢量有限元電磁計算方法，包括：對數值域內棱邊的離散化信息初始化；基于初始化的離散化信息，構建矢量有限元插值函數；選取光滑函數，采用矢量有限元插值函對光滑域內的形函數進行光滑操作，得到光滑后的形函數；結合電磁場弱形式和光滑后的形函數，得到電磁場的邊光滑的矢量有限元弱形式。通過構建電磁場的邊光滑的矢量有限元弱形式，能在不增加自由度數量的前提下，提高電磁場求解精度，節約計算資源；能適用結構化和非結構化網絡，以維持有限元在復雜幾何邊界上的解析精度，對于混合網格有較好的適配性；能改善矢量有限元在計算電磁學中的分析能力，有較好拓展性和適配性。

技術研發人員：賀志松
受保護的技術使用者：湖南邁曦軟件有限責任公司
技術研發日：
技術公布日：2024/10/14